I praksis med maskin og dyp læring Er Modellparametere egenskapene til treningsdata som vil lære seg selv under trening av klassifikatoren eller annen ML-modell. For eksempel, vekter og skjevheter, eller delt poeng I Beslutningstreet.
Modell Hyperparametere er i stedet egenskaper som styrer hele treningsprosessen. De inkluderer variabler som bestemmer nettverksstrukturen (For Eksempel Antall Skjulte Enheter) og variablene som bestemmer hvordan nettverket blir trent (for Eksempel Læringsrate). Modell hyperparametere er satt før trening(før optimalisering av vekter og bias).
Her er for eksempel noen modell innebygde konfigurasjonsvariabler:
- Læringsrate
- Antall Epoker
- Skjulte Lag
- Aktiveringsfunksjoner
Hyperparametere er viktige siden De direkte kontrollerer atferden til treningsalgoen, og har viktig innvirkning på ytelsen til modellen under trening.Å Velge passende hyperparametere spiller en nøkkelrolle i suksessen til nevrale nettverksarkitekturer, gitt virkningen på den lærte modellen. For eksempel, hvis læringsraten er for lav, vil modellen savne de viktige mønstrene i dataene; omvendt, hvis den er høy, kan den ha kollisjoner.Å Velge gode hyperparametere gir to hovedfordeler: Effektivt søk i løpet av mulige hyperparametere; Og Enklere styring Av et stort sett med eksperimenter for hyperparameter tuning.
Hyperparametere kan grovt deles inn i 2 kategorier:
1. Optimizer hyperparameters,
2. Modellspesifikke hyperparametere
de er relatert mer til optimalisering og treningsprosess.
1.1. Hvis modellen læringsrate er altfor mindre enn optimale verdier, vil det ta mye lengre tid (hundrevis eller tusenvis) av epoker for å nå en ideell tilstand. På den annen side, hvis læringshastigheten er mye større enn optimal verdi, vil den overskride den ideelle tilstanden, og algoritmen kan ikke konvergere. En rimelig startlæringsrate = 0,001.
viktig å vurdere at:
a) modellen vil ha hundrevis og tusenvis av parametere hver med sin egen feilkurve. B) feilkurver er ikke rene u-former; i stedet har de en tendens til å ha mer komplekse former med lokale minima.
1,2. Mini-Batch Størrelse:
Batchstørrelse har en effekt på ressurskravene til treningsprosessen, hastigheten og antall iterasjoner på en ikke-triviell måte.
Historisk har det vært en debatt å gjøre stokastisk trening der du passer et enkelt eksempel på datasettet til modellen, og bruker bare ett eksempel, utfører et fremoverpass, beregner feilen / backpropagate & sett justerte verdier for alle hyperparametrene. Og så gjør dette igjen for hvert eksempel i datasettet.
Eller, kanskje bedre å mate hele dataene til treningstrinnet og beregne gradienten ved hjelp av feilen generert ved å se på alle eksemplene i datasettet. Dette kalles batch trening.
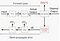
vanlig brukt teknikk i dag er å sette en mini-batch størrelse. Stokastisk Trening er når minibatch størrelse =1, Og Batch Trening er når mini-batch størrelse = Antall eksempler i treningssettet. Anbefalte startverdier for eksperimentering: 1, 2, 4, 8, 16, 32, 64, 128, 256.
en større mini-batch størrelse tillater beregnings øker som benytter matrise multiplikasjon i trening beregninger . Det kommer imidlertid på bekostning av å trenge mer minne for treningsprosessen. En mindre mini-batch størrelse induserer mer støy i feilberegninger, ofte mer nyttig i å hindre treningsprosessen fra å stoppe på lokale minima. En virkelig verdi for mini-batch størrelse= 32.Så, mens beregnings boost driver oss til å øke mini-batch størrelse, denne praktiske algoritmisk fordel incentivizes å faktisk gjøre det mindre.
1,3. Antall Epoker:
for å velge riktig antall epoker for treningstrinnet, er metriske vi bør være oppmerksom på Valideringsfeilen.
den intuitive manuelle måten er å få modellen til å trene for så mange antall iterasjoner så lenge valideringsfeilen fortsetter å synke.Det er en teknikk som kan brukes Som Heter Tidlig Stopp for å bestemme når man skal slutte å trene modellen; det handler om å stoppe treningsprosessen dersom valideringsfeilen ikke har blitt bedre de siste 10 eller 20 epokene.
2. Modell Hyperparameters
De er mer involvert i strukturen til modellen:
2.1. Antall skjulte enheter:
Antall skjulte enheter er en av de mer mystiske hyperparametrene. La oss huske at nevrale nettverk er universelle funksjonstilnærmere, og for at de skal lære å tilnærme en funksjon (eller en prediksjonsoppgave) , må de ha nok kapasitet til å lære funksjonen. Antall skjulte enheter er det viktigste målet for modellens læreevne.
for en enkel funksjon, kan det trenge færre antall skjulte enheter. Jo mer kompleks funksjonen er, desto mer læringskapasitet vil modellen trenge.
litt mer antall enheter da optimal antall er ikke et problem, men et mye større antall vil føre til overfitting (dvs.hvis du gir en modell med for mye kapasitet, kan det ha en tendens til å overfit, prøver å «huske» datasettet, derfor påvirker kapasiteten til å generalisere)
2.2. Første skjulte lag:
En annen heuristisk som involverer det første skjulte laget er at å sette antall skjulte enheter større enn antall innganger har en tendens til å muliggjøre bedre resultater i antall oppgaver, ifølge empirisk observasjon.
2.3. Antall lag:
det er ofte slik at 3-lags Nevrale Nett vil overgå en 2-lags en. Men å gå enda dypere hjelper sjelden mye mer. (unntak Er Convolutional Nevrale Nettverk, hvor jo dypere de er, desto bedre utfører de).
Optimaliseringsteknikker For Hyperparametere
prosessen med å finne de mest optimale hyperparametrene i maskinlæring kalles hyperparameteroptimalisering.
Vanlige algoritmer inkluderer:
- Grid Search
- Tilfeldig Søk
- Bayesiansk Optimalisering
Grid Search
grid search Er en tradisjonell teknikk for å implementere hyperparametere. Det handler litt om brute force alle kombinasjoner. Grid søk krever opprettingto sett med hyperparametere:
- Lærings Rate
- Antall Lag
Grid søk tog algoritmen for alle kombinasjoner ved hjelp av to sett med hyperparameters (læring rate og antall lag) og måler ytelsen ved hjelp av kryss-validering teknikk. Denne valideringsteknikken sikrer at den trente modellen får de fleste mønstrene fra datasettet (en av de beste metodene for å utføre validering ved å bruke «K-Fold Cross Validation» som bidrar til å gi rikelig med data for trening av modellen og rikelig med data for valideringer).Grid-søkemetoden er en enklere algoritme å bruke, men den lider hvis data har høyt dimensjonalt rom kalt curse of dimensionality.
Tilfeldig søk
tilfeldig prøver søkeområdet Og evaluerer sett fra en spesifisert sannsynlighetsfordeling. I stedet for å prøve å sjekke alle 100 000 prøver, kan vi for eksempel sjekke 1000 tilfeldige parametere.ulempen med å bruke den tilfeldige søkealgoritmen er imidlertid at den ikke bruker informasjon fra tidligere eksperimenter for å velge neste sett. Videre er det vanskelig å forutsi neste av eksperimenter.

bayesiansk optimalisering
hyperparameterinnstilling maksimerer ytelsen til modellen på et valideringssett. ML algos krever ofte finjustering av modell hyperparametere. Dessverre kalles denne tuningen ofte ‘svart funksjon’ fordi den ikke kan skrives inn i en formel (derivater av funksjonen er ukjente).
en mer tiltalende måte å optimalisere & finjustere hyperparametere innebærer å aktivere automatisert modell tuning tilnærming-for eksempel ved Hjelp Av Bayesiansk optimalisering. Modellen som brukes til å tilnærme objektivfunksjonen kalles surrogatmodell. En populær surrogatmodell for Bayesiansk optimalisering er Gaussisk prosess (GP). Bayesiansk optimalisering fungerer vanligvis ved å anta at den ukjente funksjonen ble samplet fra En Gaussisk Prosess (GP) og opprettholder en bakre fordeling for denne funksjonen når observasjoner gjøres.
Det er to store valg som skal gjøres Når Du utfører Bayesiansk optimalisering:
- Velg prior over funksjoner som vil uttrykke antagelser om funksjonen blir optimalisert. For dette velger Vi Gaussisk Prosess før;
- Neste må vi velge en oppkjøpsfunksjon som brukes til å konstruere en bruksfunksjon fra modellen bakre, slik at vi kan bestemme neste punkt å evaluere.En Gaussisk prosess definerer den tidligere fordelingen over funksjoner som kan konverteres til en bakre overfunksjoner når vi har sett noen data. Den Gaussiske prosessen bruker Kovariansmatrise for å sikre at verdier som er tett sammen. Kovariansmatrisen sammen med en gjennomsnittlig µ-funksjon for å utføre forventet verdi ƒ(x) definerer En Gaussisk prosess.
1. Gaussisk prosess vil bli brukt som en prior For Bayesian inferens;
2. Ved å beregne den bakre delen kan den brukes til å gjøre spådommer for usynlige testtilfeller.

Acquisition Function
Introducing sampling data into the search space is done by acquisition functions. It helps to maximize the acquisition function to determine the next sampling point. Populære oppkjøpsfunksjoner er
- Maksimal Sannsynlighet For Forbedring (MPI)
- Forventet Forbedring (EI)
- Øvre Konfidensgrense (UCB)
Den Forventede Forbedringen (EI) er en populær Og definert som:
ei(x)=𝔼
der ƒ(x ) er det nåværende optimale settet med hyperparametere. Maksimering av hyperparametrene vil bli bedre ved ƒ.
