Introduksjon Til Bevegelsesestimering med Optisk Strømning

i denne opplæringen dykker vi inn i grunnleggende For Optisk Strømning, ser på noen av applikasjonene og implementerer sine to hovedvarianter(sparsom og tett). Vi diskuterer også kort nyere tilnærminger ved hjelp av dyp læring og lovende fremtidige retninger.

nylige gjennombrudd i datasynsforskning har gjort det mulig for maskiner å oppfatte omverdenen gjennom teknikker som objektdeteksjon for å oppdage forekomster av objekter som tilhører en bestemt klasse og semantisk segmentering for pikselvis klassifisering.

men for å behandle videoinngang i sanntid, adresserer de fleste implementeringer av disse teknikkene bare relasjoner av objekter innenfor samme ramme \((x, y)\) uten hensyn til tidsinformasjon \((t)\). Med andre ord vurderer de hver ramme uavhengig, som om de er helt urelaterte bilder, for hvert løp. Men hva om vi trenger forholdet mellom sammenhengende rammer, for eksempel vil vi spore bevegelsen av kjøretøy over rammer for å estimere sin nåværende hastighet og forutsi posisjonen i neste ramme?

eller, alternativt, hva om vi trenger informasjon om menneskelige positur relasjoner mellom påfølgende rammer for å gjenkjenne menneskelige handlinger som bueskyting, baseball og basketball?

i denne opplæringen vil vi lære hva optisk flyt er, hvordan å implementere sine to hovedvarianter (sparsom og tett), og også få et stort bilde av nyere tilnærminger som involverer dyp læring og lovende fremtidige retninger.

Hva Er Optisk Flyt?
Implementere Sparsom Optisk Flyt
Implementere Tett Optisk Flyt
Dyp læring og utover

Hva er optisk flyt?

La oss begynne med en høyt nivå forståelse av optisk flyt. Optisk flyt er bevegelsen av objekter mellom påfølgende sekvensrammer, forårsaket av den relative bevegelsen mellom objektet og kameraet. Problemet med optisk strømning kan uttrykkes som:

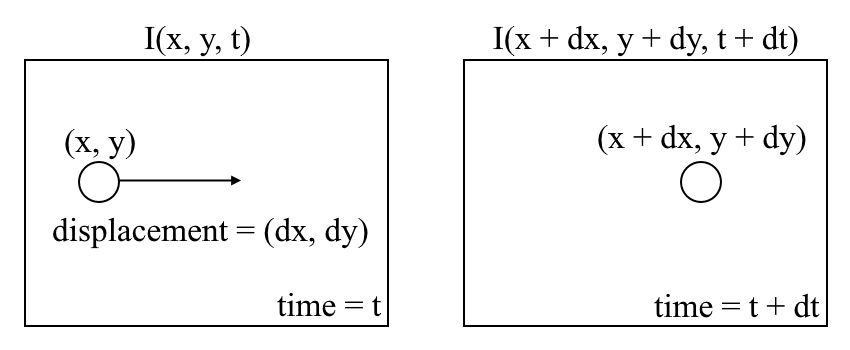
hvor mellom påfølgende rammer kan vi uttrykke bildeintensiteten \((I)\) som en funksjon av rom \((x, y)\) og tid \((t)\). Med andre ord, hvis vi tar det første bildet \(i (x, y, t)\) og flytter pikslene med \((dx, dy)\) over \(t\) tid, får vi det nye bildet \(i (x + dx, y + dy, t + dt)\).

Først antar Vi at pikselintensiteter av et objekt er konstant mellom påfølgende rammer.

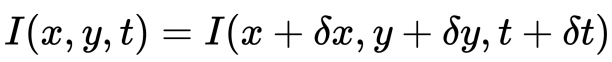
For Det Andre tar Vi Taylor-Serien Tilnærming AV RHS og fjerner vanlige termer.

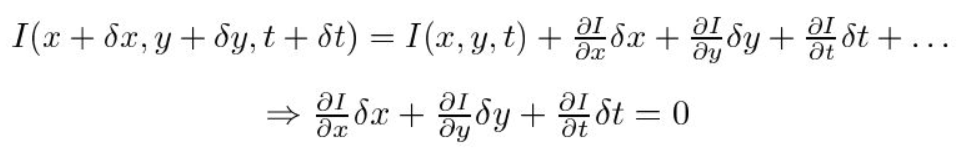
Tredje deler vi med \(dt\) for å utlede den optiske strømningsligningen:

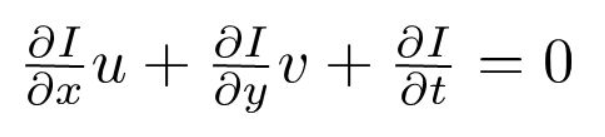
hvor \(u = dx/dt\) og \(v = dy / dt\).

\(dI/ dx, dI / dy\) og \(dI/dt\) er bildegradienter langs den horisontale aksen, den vertikale aksen og tiden. Derfor konkluderer vi med problemet med optisk strømning, det vil si å løse \(u (dx/ dt)\) og \(v (dy/dt)\) for å bestemme bevegelse over tid. Du kan legge merke til at vi ikke direkte kan løse den optiske strømningsligningen for \(u\) og\ (v\) siden det bare er en ligning for to ukjente variabler. Vi vil implementere noen metoder som Lucas-Kanade-metoden for å løse dette problemet.

Sparsom vs Tett Optisk Strømning

Sparsom optisk strømning gir strømningsvektorer av noen «interessante funksjoner» (si få piksler som viser kantene eller hjørnene til et objekt) innenfor rammen mens Tett optisk strømning, som gir strømningsvektorer av hele rammen (alle piksler) – opp til en strømningsvektor per piksel. Som du ville ha gjettet, Har Tett optisk strøm høyere nøyaktighet på bekostning av å være sakte/beregningsmessig dyrt.

Implementering Av Sparsom Optisk Strøm

Sparsom optisk strøm velger et sparsomt funksjonssett med piksler (f.eks. interessante funksjoner som kanter og hjørner) for å spore hastighetsvektorer (bevegelse). De ekstraherte funksjonene sendes i optisk strømningsfunksjon fra ramme til ramme for å sikre at de samme punktene spores. Det finnes ulike implementeringer av sparsom optisk flyt, inkludert Lucas-Kanade-metoden, Horn-Schunck-metoden, Buxton-Buxton-metoden og mer. Vi vil bruke Lucas-Kanade-metoden Med OpenCV, et åpen kildekode-bibliotek med datasynalgoritmer, for implementering.

Sette opp miljøet

hvis Du ikke Allerede Har OpenCV installert, åpne Terminal og kjøre:

pip install opencv-python

nå klone opplæringen depotet ved å kjøre:

git clone https://github.com/chuanenlin/optical-flow.git

neste, åpne sparse-starter.py med teksteditoren din. Vi skal skrive all koden i Denne Python-filen.

Konfigurere OpenCV for å lese en video og sette opp parametere

Shi-Tomasi Corner Detector-velge piksler for å spore

for implementering av sparsom optisk strøm, sporer vi bare bevegelsen til et funksjonssett med piksler. Funksjoner i bilder er interessepunkter som presenterer rik bildeinnholdsinformasjon. Slike funksjoner kan for eksempel være punkter i bildet som er uforanderlige til oversettelse, skala, rotasjon og intensitetsendringer, for eksempel hjørner.

Shi-Tomasi Corner Detector er svært lik Den populære Harris Corner Detector som kan implementeres av følgende tre prosedyrer:

1. Bestem vinduer (små bilde patcher) med store gradienter(variasjoner i bildeintensitet) når oversatt i både \(x\) og \(y\) retninger.
2. for hvert vindu beregner du en poengsum \(R\).
3. avhengig av verdien av \(R\), er hvert vindu klassifisert som en flat, kant eller hjørne.

hvis du vil vite mer om en trinnvis matematisk forklaring Av Harris Corner Detector, vær så snill å gå gjennom disse lysbildene.

Shi og Tomasi gjorde senere en liten, men effektiv modifikasjon Av Harris Corner Detector i deres Papir Gode Funksjoner For Å Spore.

modifikasjonen er til ligningen der score \(R\) beregnes. I Harris Corner Detektoren er scoring-funksjonen gitt av:

$$
\start{array}{c}{R=\operatorname{det} M-k(\operatorname{trace} M)^{2}}\newline \
{\operatorname{det} M=\lambda_{1} \lambda_{2}}\end {array}
$$

i stedet foreslo shi-tomasi scoringsfunksjonen Som:

$$
r=\min\left (\lambda_{1},\lambda_{2}\right)
$$

som i utgangspunktet betyr at hvis\(r\) er større enn en terskel, er den klassifisert som et hjørne. Følgende sammenligner scoringsfunksjonene Til Harris (venstre) og Shi-Tomasi(høyre) i \(λ1-λ2\) – rommet.

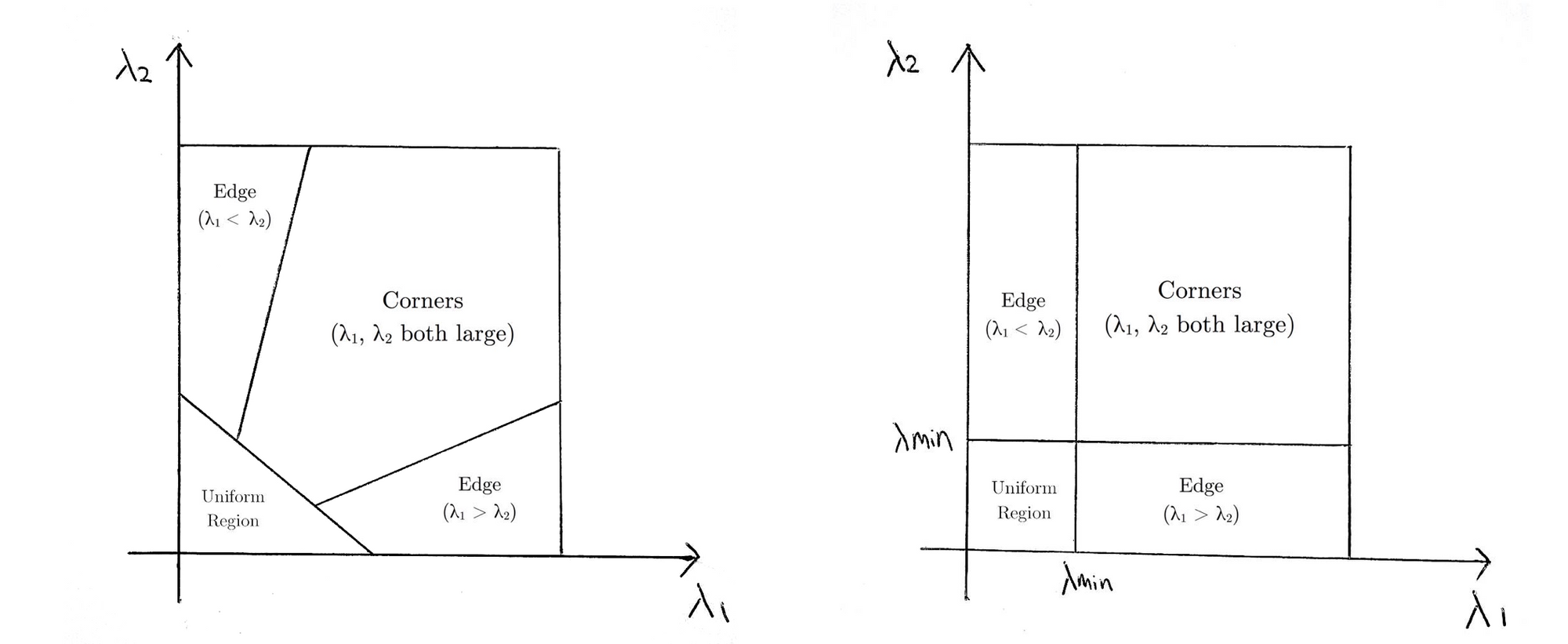
For Shi-Tomasi er kun Vinduet klassifisert som hjørne når \(λ1\) og \(λ2\) er over en minimumsgrense \(λ\).

dokumentasjonen Av Opencvs implementering Av Shi-Tomasi via goodFeaturesToTrack() finner du her.

Sporing Av Bestemte Objekter

det kan være scenarier der du bare vil spore et bestemt objekt av interesse (si sporing av en bestemt person) eller en kategori av objekter (som alle 2 hjulkjøretøy i trafikken). Du kan enkelt endre koden for å spore pikslene til objektet(e) du vil ha ved å endreprev variabelen.

du kan også kombinere Objektgjenkjenning med denne metoden for å bare beregne strømmen av piksler i de oppdagede markeringsboksene. På denne måten kan du spore alle objekter av en bestemt type/kategori i videoen.

Lucas-Kanade: Sparsom Optisk Flyt

Lucas og Kanade foreslo en effektiv teknikk for å estimere bevegelsen av interessante funksjoner ved å sammenligne to påfølgende rammer I papiret En Iterativ Bilderegistreringsteknikk med En Applikasjon Til Stereosyn. Lucas-Kanade-metoden fungerer under følgende forutsetninger:

1. To påfølgende rammer er adskilt av en liten tidsøkning (\(dt\)) slik at objekter ikke forskyves betydelig (med andre ord, metoden fungerer best med sakte bevegelige objekter).
2. en ramme skildrer en «naturlig» scene med teksturerte objekter som viser gråtoner som endres jevnt.

Først under disse forutsetningene kan vi ta et lite 3×3-vindu (nabolag) rundt funksjonene oppdaget Av Shi-Tomasi og anta at alle ni punkter har samme bevegelse.

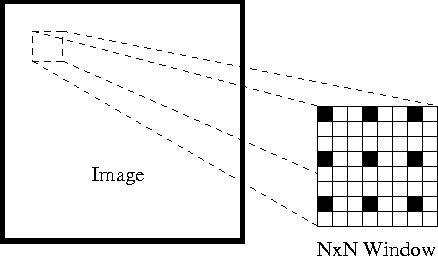
dette kan representeres som

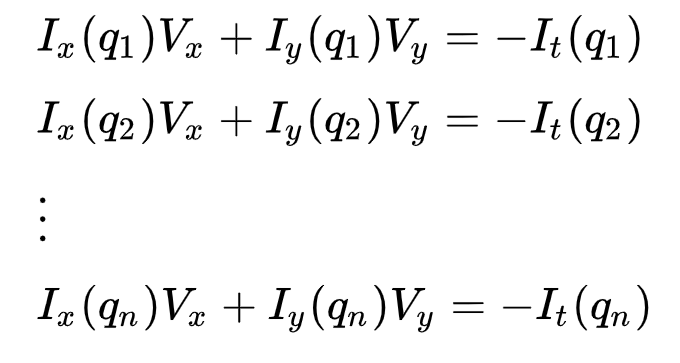
hvor \(q_1, q_2, …, q_n\) betegner pikslene Inne i vinduet (f.eks \(n\) = 9 for et 3×3-vindu) og \(i_x(q_i)\), \(i_y(q_i)\), og \(i_t(q_i)\) Betegner Partielle derivater av bilde \(i\) med hensyn til posisjon \((x, y)\) og tid \(t\), for piksel \(q_i\) på nåværende tidspunkt.

dette er Bare Den Optiske Strømningsligningen (som vi beskrev tidligere) for hver av n-pikslene.

settet av ligninger kan representeres i følgende matriseform hvor \(av = b\):

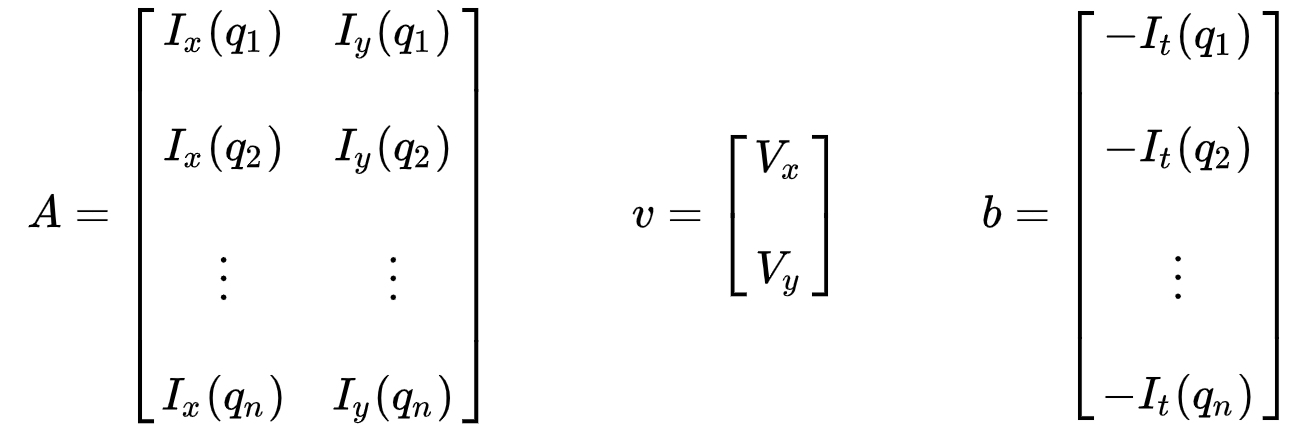
Legg merke til at tidligere (se «hva er optisk Flyt?»seksjon), møtte vi spørsmålet om å måtte løse for to ukjente variabler med en ligning. Vi står nå overfor å måtte løse for to ukjente (\(V_x\) og \(V_y\)) med ni ligninger, som er overbestemt.

For Det Andre, for å løse det overbestemte problemet, bruker vi minste kvadrater som passer for å oppnå følgende to-ligning-to-ukjent problem:

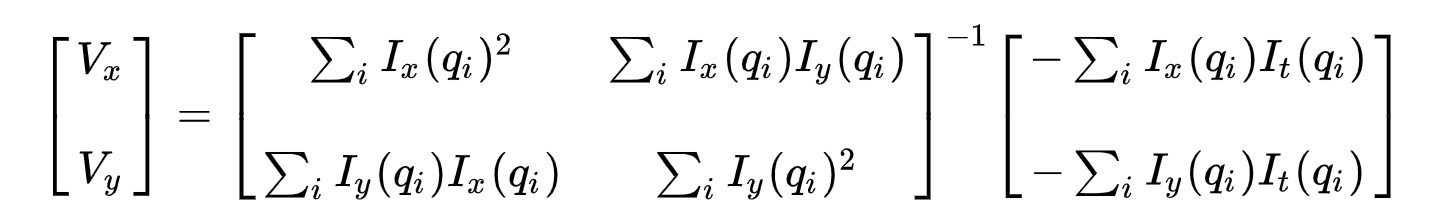
hvor \(vx = u = dx/dt\) betegner bevegelsen av \(x\) over tid og \(vy = v = dy/dt\) betegner bevegelsen av y over tid. Løsning for de to variablene fullfører det optiske strømningsproblemet.

I et nøtteskall identifiserer vi noen interessante funksjoner for å spore og iterativt beregne de optiske strømningsvektorer av disse punktene. Imidlertid fungerer bruk Av Lucas-Kanade-metoden bare for små bevegelser (fra vår første antagelse) og mislykkes når det er stor bevegelse. Derfor vedtar OpenCV-implementeringen Av Lucas-Kanade-metoden pyramider.

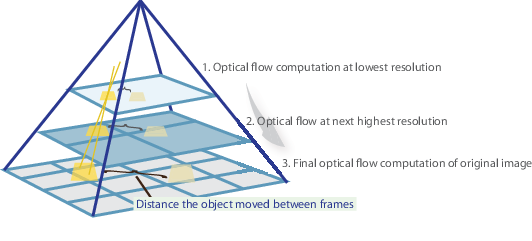
i et høyt nivå visning, små bevegelser er neglisjert som vi går opp pyramiden og store bevegelser er redusert til små bevegelser-vi beregne optisk flyt sammen med skala. En omfattende matematisk forklaring Av OpenCV implementering kan finnes I Bouguet notater og dokumentasjon Av OpenCV implementering Av Lucas-Kanade metoden via calcOpticalFlowPyrLK() kan bli funnet her.

Visualiserer

Og det er det! Åpne Terminal og kjør

python sparse-starter.py

for å teste din sparsomme optiske flytimplementering. 👏

i tilfelle du har gått glipp av noen kode, kan du finne hele koden i sparse-solution.py.

Implementere Tett Optisk Flyt

vi har tidligere beregnet den optiske strømmen for et sparsomt funksjonssett med piksler. Tett optisk flyt forsøker å beregne den optiske strømningsvektoren for hver piksel i hver ramme. Selv om slike beregninger kan være tregere, gir det et mer nøyaktig resultat og et tettere resultat egnet for applikasjoner som læringsstruktur fra bevegelse og videosegmentering. Det finnes ulike implementeringer av tett optisk strømning. Vi vil bruke Farneback-metoden, en Av De mest populære implementeringene, Med Å bruke OpenCV, et åpen kildekodebibliotek med datasynalgoritmer, for implementering.

Sette opp miljøet

hvis du ikke allerede har gjort det, følg Trinn 1 for å implementere sparsom optisk flyt for å sette opp miljøet ditt.

neste, åpne dense-starter.py med teksteditoren din. Vi skal skrive all koden i Denne Python-filen.

Konfigurere OpenCV for å lese en video

Farneback Optisk Flyt

Gunnar Farneback foreslo en effektiv teknikk for å estimere bevegelsen av interessante funksjoner ved å sammenligne to påfølgende rammer I sin papir To-Ramme Bevegelse Estimering Basert På Polynomisk Ekspansjon.for Det Første tilnærmer metoden vinduene (se Lucas Kanade-delen av sparsom optisk flytimplementering for flere detaljer) av bilderammer ved kvadratiske polynomer gjennom polynomisk ekspansjonstransformasjon. For det andre, ved å observere hvordan polynomet transformerer under oversettelse (bevegelse), er en metode for å estimere forskyvningsfelt fra polynom ekspansjonskoeffisienter definert. Etter en rekke forbedringer beregnes tett optisk strømning. Farneback papir er ganske konsis og grei å følge så jeg anbefaler å gå gjennom papiret hvis du ønsker en større forståelse av sin matematiske avledning.

For Opencvs implementering beregner den størrelsen og retningen av optisk strømning fra et 2-kanals utvalg av strømningsvektorer \((dx/ dt, dy/ dt)\), det optiske strømningsproblemet. Det visualiserer deretter vinkelen (retning) av strømning av fargetone og avstanden (størrelsen) av strømning etter verdi AV HSV-fargepresentasjon. Styrken TIL HSV er alltid satt til maksimalt 255 for optimal synlighet. Dokumentasjonen Av Opencvs implementering Av Farneback-metoden via calcOpticalFlowFarneback() finner du her.

Visualiserer

Og det er det! Åpne Terminal og kjør

python dense-starter.py

for å teste din tette optiske flytimplementering. 👏

i tilfelle du har gått glipp av noen kode, kan du finne hele koden i dense-solution.py.

Optisk Flyt ved Hjelp Av Dyp Læring

mens problemet med optisk flyt historisk har vært et optimaliseringsproblem, har nyere tilnærminger ved å bruke dyp læring vist imponerende resultater. Vanligvis tar slike tilnærminger to videorammer som inngang for å sende ut den optiske strømmen( fargekodet bilde), som kan uttrykkes som:

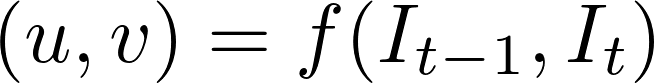
hvor \(u\) er bevegelsen i \(x\) retning, \(v\) er bevegelsen i \(y\) retning, og \(f\) er et nevralt nettverk som tar i to påfølgende rammer \(i_{t-1}\) (ramme på tid = \(t-1)\) og \(i_t\) (ramme på tid = \(t-1)\) og \ (i_t\) (ramme på tid = \ (t)\) som inngang.

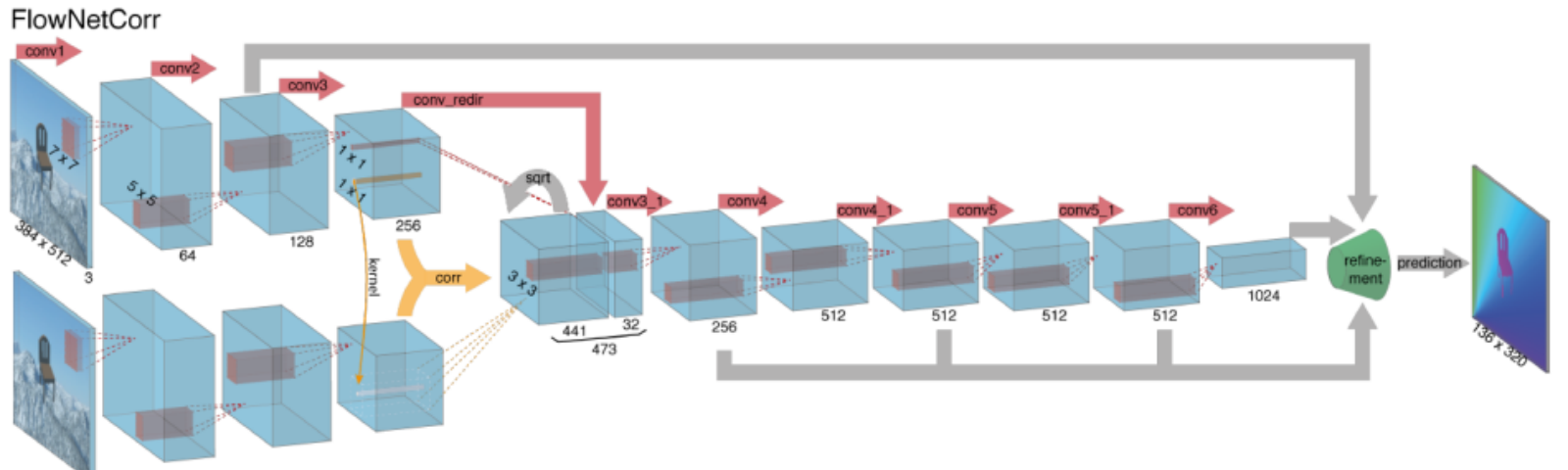
Databehandling optisk flyt med dype nevrale nettverk krever store mengder treningsdata som er spesielt vanskelig å oppnå. Dette skyldes at merking av videoopptak for optisk strøm krever nøyaktig å finne ut nøyaktig bevegelse av hvert punkt i et bilde til subpixel nøyaktighet. For å løse problemet med merking av treningsdata, brukte forskere datagrafikk for å simulere massive realistiske verdener. Siden verdenene genereres av instruksjon, er bevegelsen av hvert punkt i et bilde i en videosekvens kjent. NOEN eksempler på SLIKE inkluderer MPI-Sintel, en åpen kildekode CGI-film med optisk flytmerking gjengitt for ulike sekvenser, Og Flygende Stoler, et datasett av mange stoler som flyr over tilfeldige bakgrunner, også med optisk flytmerking.

Å Løse optiske strømningsproblemer med dyp læring Er et ekstremt hett tema for øyeblikket, med varianter Av FlowNet, SPyNet, PWC-Net og mer hver utkonkurrerer hverandre på ulike referanser.

Optisk Flytapplikasjon: Semantisk Segmentering

det optiske strømningsfeltet er en enorm mengde informasjon for den observerte scenen. Som teknikker for nøyaktig å bestemme optisk flyt bedre, er det interessant å se anvendelser av optisk flyt i krysset med flere andre grunnleggende datamaskinen visjoner oppgaver. For eksempel er oppgaven med semantisk segmentering å dele et bilde i serie av regioner som svarer til unike objektklasser, men tett plasserte objekter med identiske teksturer er ofte vanskelig for segmenteringsteknikker for enkeltrammer. Hvis objektene plasseres separat, kan imidlertid de distinkte bevegelsene til objektene være svært nyttige der diskontinuitet i det tette optiske strømningsfeltet tilsvarer grenser mellom objekter.

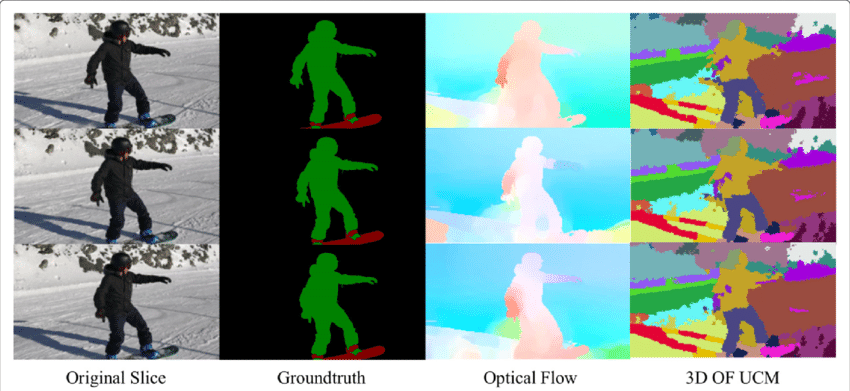
Optisk Flyt søknad: Objekt Deteksjon& Sporing

En annen lovende anvendelse av optisk flyt kan være med objekt deteksjon og sporing eller, i et høyt nivå form, mot å bygge sanntids kjøretøy sporing og trafikk analyse systemer. Siden sparsom optisk strøm benytter sporing av interessepunkter, kan slike sanntidssystemer utføres av funksjonsbaserte optiske strømningsteknikker fra enten fra et stasjonært kamera eller kameraer festet til kjøretøy.

Konklusjon

I Utgangspunktet fungerer optiske strømningsvektorer som input til et myriade av oppgaver på høyere nivå som krever sceneforståelse av videosekvenser, mens disse oppgavene kan fungere som byggesteiner til enda mer komplekse systemer som ansiktsuttrykksanalyse, autonom kjøretøynavigasjon og mye mer. Nye applikasjoner for optisk flyt som ennå ikke er oppdaget, er begrenset bare av oppfinnsomheten til designerne.Lat til å kode, vil ikke bruke På Gpuer? Gå over Til Nanonets og bygg datasynsmodeller gratis!