Uovervåket Bayesiansk Slutning (redusere dimensjoner og grave funksjoner)

bilde av julius drost på unsplash
endelig, øyeblikket du alle har ventet på, den neste i vår unsupervised Bayesian inference Series: vår (ikke så) dyp dykk inn I Sobel-Operatøren.
en virkelig magisk kantdeteksjonsalgoritme, det muliggjør ekstraksjon av funksjoner på lavt nivå og dimensjonsreduksjon, noe som i hovedsak reduserer støy i bildet. Det har vært spesielt nyttig i ansiktsgjenkjenningsprogrammer.1968 love child Av Irwin Sobel Og Gary Feldman (Stanford Artificial Intelligence Laboratory), denne algoritmen var inspirasjonen til mange moderne kantdeteksjonsteknikker. Ved å vikle to motstående kjerner eller masker over et gitt bilde (f. eks. se nedenfor-venstre) (hver i stand til å oppdage enten horisontale eller vertikale kanter), kan vi skape en mindre støyende, utjevnet representasjon (se nedenfor-høyre).
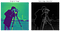
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel verdier (vanligvis luminans) ved å differensiere forskjellen mellom hver piksel (ankerpiksel) og dens omkringliggende piksler (i hovedsak tilnærmet derivatet av et bilde).
dette resulterer i utjevning av det opprinnelige bildet og gir en lavere dimensjonsutgang, hvor lavt nivå geometriske egenskaper kan ses tydeligere. Disse utgangene kan da brukes som innganger til mer komplekse klassifiseringsalgoritmer, eller som eksempler brukt til uovervåket probabilistisk clustering via Kullback-Leibler Divergence (KLD) (som sett i min siste blogg PÅ LBP).
Generering av vår nedre dimensjonsutgang krever at vi tar derivatet av bildet. Først beregner vi derivatet i både x og y retninger. Vi lager to 3×3 kjerner (se matriser), med nuller langs midten av den tilsvarende aksen, to i midtfirkantene vinkelrett på den sentrale null og de i hver av hjørnene. Hver av de ikke-nullverdiene skal være positiv på toppen / til høyre for nullene (avhengig av akse) og negativ på deres tilsvarende side. Disse kjernene heter Gx og Gy.
disse vises i formatet:
disse kjernene vil da vikle seg over bildet vårt, og plassere den sentrale pikselen til hver kjerne over hver piksel i bildet. Vi bruker matrisemultiplikasjon til å beregne intensitetsverdien til en ny tilsvarende piksel i et utgangsbilde, for hver kjerne. Derfor ender vi opp med to utgangsbilder (en for hver kartesisk retning).
målet er å finne forskjellen/endringen mellom pikselen i bildet og alle piksler i gradientmatrisen (kjernen) (Gx og Gy). Mer matematisk kan dette uttrykkes som.
side notat:
vi er teknisk ikke convolving noe. Selv om vi liker å referere til ‘convolutions’ I AI og maskinlæringssirkler, vil en convolution innebære å vende det opprinnelige bildet. Matematisk sett, når vi refererer til konvolutter, beregner vi virkelig krysskorrelasjonen mellom hvert 3×3-område av inngangen og masken for hver piksel. Utgangsbildet er den generelle kovariansen mellom masken og inngangen. Slik oppdages kantene.
Tilbake til Vår Sobel forklaring…
de beregnede verdiene for hver matrisemultiplikasjon mellom masken og 3×3-delen av inngangen summeres for å produsere den endelige verdien for pikselen i utgangsbildet. Dette genererer et nytt bilde som inneholder informasjon om tilstedeværelsen av vertikale og horisontale kanter i det opprinnelige bildet. Dette er en geometrisk funksjonsrepresentasjon av det opprinnelige bildet. Videre, fordi denne operatøren er garantert å produsere samme utgang hver gang, tillater denne teknikken stabil kantdeteksjon for bildesegmenteringsoppgaver.
fra disse utgangene kan vi beregne både gradientstørrelsen og gradientretningen (ved hjelp av arctangentoperatøren) på en gitt piksel (x, y):
fra dette kan Vi fastslå At disse pikslene med store størrelser er mer sannsynlig å være en kant i bildet,mens retningen informerer oss om kantretningen (selv om retningen ikke er nødvendig for å generere produksjonen vår).
en enkel implementering:
her er en enkel implementering Av Sobel-operatøren i python (ved Hjelp Av NumPy) for å gi deg en følelse for prosessen (for alle dere spirende kodere der ute).
denne implementeringen er en python-variant av wikipedia-pseudokodeeksemplet, med sikte på å vise hvordan du kan implementere denne algoritmen, samtidig som du demonstrerer de ulike trinnene i prosessen.
Hvorfor bryr vi oss?
selv om gradienttilnærmingen produsert av denne operatøren er relativt rå, gir den en ekstremt beregningsmessig effektiv metode for å beregne kanter, hjørner og andre geometriske egenskaper av bilder. I sin tur har det banet vei for en rekke dimensjonsreduksjons-og funksjonsutvinningsteknikker ,For Eksempel Lokale Binære Mønstre (se min andre blogg for mer informasjon om denne teknikken).Å Stole på utelukkende geometriske egenskaper risikerer å miste viktig informasjon under kodingen av dataene våre, men avveiningen er det som muliggjør rask forbehandling av dataene og i sin tur rask trening. Derfor er denne teknikken spesielt nyttig i scenarier der tekstur og geometriske funksjoner kan betraktes som svært viktig i å definere input. Dette er grunnen til at ansiktsgjenkjenning kan fullføres med en relativt høy grad av nøyaktighet ved Hjelp Av Sobel-operatøren. Imidlertid kan denne teknikken ikke være det beste valget hvis du prøver å klassifisere eller gruppere innganger som bruker farge som deres viktigste differensierende faktor.
denne metoden er fortsatt svært effektiv for å få en lavdimensjonal representasjon av geometriske funksjoner og et utmerket utgangspunkt for dimensjonalitet og støyreduksjon, før du bruker andre klassifiserere eller for Bruk I Bayesianske slutningsmetoder.