Postet juni 2008.
den andre av to kolonner på matematikken til oppmåling (den første er her). …
Bill Casselman
Universitetet I British Columbia, Vancouver, Canada
cass at math.ubc.ca
John Eggers
Universitetet I California, San Diego
jeggers ved ucsd.edu
 E-Post til en venn |
 skriv ut denne artikkelen |
et planimeter er et bordinstrument for måling av områder, vanligvis områdene med uregelmessige Områder på et kart eller fotografi. De var en gang vanlige, men har nå i stor grad blitt erstattet av digitale verktøy.
følgende bilde gir en ide om oppsettet. Polarmen roterer fritt rundt stangen, som er festet på bordet. Sporarmen roterer rundt pivoten, som er der den knytter seg til polararmen. Du sporer en kurve i retning med urviseren med sporeren, og når du gjør det, ruller målehjulet sammen, og den totale avstanden det ruller, akkumuleres på skiven. Støttehjulet holder ting fra flopping over. På slutten leser du av et nummer fra skiven, og etter multiplikasjon med en faktor avhengig av den spesielle konfigurasjonen av planimeteret, får du området inne i kurven.
neste figur gir deg en bedre oversikt over mekanismen.
vi kaller vognen montering av hjul, dial og pivot. I neste bilde får du en bedre titt på det, og kan se ormen stasjonen som får skiven til å rotere som målehjulet beveger seg.
Her er diagrammet av det opprinnelige planimeteret, fra Artikkelen Av Jakob Amsler som introduserte det:
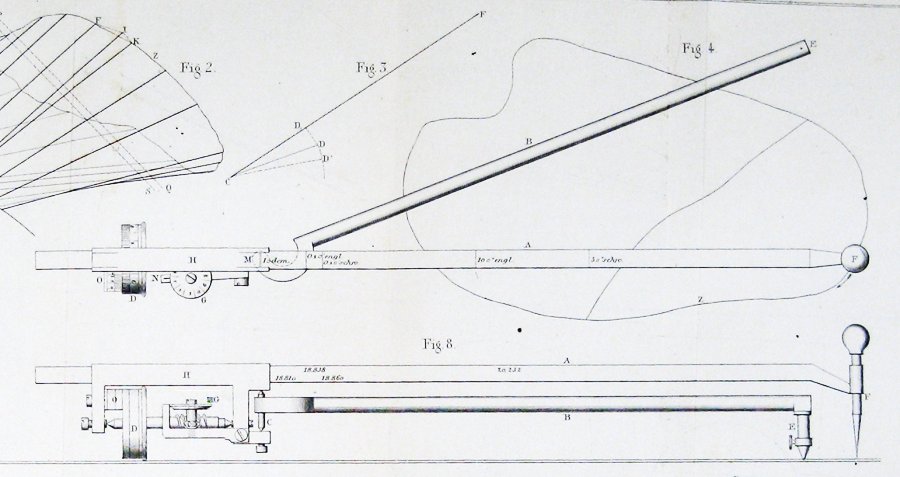
Hvordan kan en så enkel ting måle områder?
Planimeterets Geometri
bevegelsen med urviseren til planimeteret er retningen motsatt hva matematikere har bestemt skal være positiv rotasjon. I stedet for å bryte denne konvensjonen, skal vi jobbe fra nå av med en matematikers planimeter, der du beveger deg mot klokka. Som andre matematikeres fantasier, er det ingen på planeten!
Det er noen begrensninger på hvordan du plasserer planimeteret med hensyn til kurven du vil spore. Vognen kan skyves langs sporarmen, men i alle tilfeller er lengden l på sporarmen mindre enn lengden r på stangarmen. Dette betyr at tracer kan aldri komme innenfor en avstand r-l av stangen. På den annen side, når den er helt utvidet, kan sporeren aldri nå utover r + l. så kurven som skal spores må ligge innenfor ringrommet mellom to sirkler, en med radius r-l, den andre r + l.
faktisk bør det bli klart i et øyeblikk at armene aldri skal bli helt forlenget, så kurven som skal spores må ligge helt inne i ringrommet. Videre er normalt stangen plassert på utsiden av kurven.
For et gitt punkt i ringrommet er det nøyaktig to mulige konfigurasjoner av planimeteret som plasserer sporeren på det punktet. Å velge ett punkt eller det andre betyr å velge et tegn på en kvadratrot. Vi kaller dette å velge en orientering for planimeteret. Det er positivt hvis kvadratroten er positiv. Når en orientering er valgt, vil den forbli den samme med mindre armen er helt forlenget. Dette må aldri skje. Så lenge kurven din er helt innenfor ringrommet, vil konfigurasjonene av planimeteret variere jevnt og unikt med sporets sti.
den neste tingen å gjøre er å forstå noen ting om bevegelsen av målehjulet. Som det følgende bildet viser, hvis hjulet beveger seg i en rett linje a avstand C, roterer hjulet gjennom en vinkel θ = C/R hvor R er dens radius.
så det er virkelig sant at rotasjonen av hjulet og avstanden som er reist av sporarmen, har noe forhold til hverandre. Men dette forholdet er litt subtilt. Hvis armen bare beveger seg rett fram en avstand C, området feid ut vil være lC, men hvis det skifter parallelt med seg selv området feid ut vil være 0. I det første tilfellet vil et punkt på hjulets omkrets bevege seg avstand C. i andre tilfelle vil hjulet ikke bevege seg i det hele tatt. Og hvis armen oversettes skråt, vil hjulet rotere en avstand som er lik høyden til parallellogrammet dekket av armen. I alle tilfeller hvor armen oversettes parallelt med seg selv, området feid ut av delen av sporarmen mellom pivot og spor vil være lik lC, Hvor C er avstanden målt ved rotasjon av hjulet. Dette er det grunnleggende faktum om armens bevegelse til bevegelsen av målehjulet.
måten å frase dette nøyaktig er at uansett hvordan armen beveger seg, er avstanden målt av hjulet stiintegralet
Hvor Γ er banen som er reist av armpunktet der målehjulet er festet, n er enhetsvektoren vinkelrett på armens retning.arm når som helst, og t er enhetsvektoren som peker i kjøreretningen (slik at for eksempel hvis armen beveger seg parallelt med seg selv, er prikkproduktet av n og t 0).
Guldins Teorem
Neste skal vi prøve å gjøre planimeterets oppførsel intuitivt klart, men først skal vi se på en spesiell type planimeter, og i dette tilfellet bevise et mer generelt resultat. Anta at vi tar en enkelt fritt bevegelig arm med lengde l og legger til et målehjul med radius R midt i midten.
så beveger vi armen rundt på flyet. Hvis målehjulet roterer gjennom en total vinkel på θ radianer når armen beveger seg rundt, er avstanden et punkt på omkretsens bevegelser C = θ.
Guldins Teorem. I denne situasjonen er det totale arealet feid ut av armen produktet lC.
Området her tolkes med et tegn. Hvis armen bare roterer rundt midten, går den ene halvdelen av armen fremover og den andre bakover, og de to avbryter.
Vi har allerede sett At Guldins påstand er gyldig i tilfelle armen bare oversetter. Selvfølgelig skjer dette ikke alltid – armen kan rotere når den beveger seg, så vel som å oversette. Men vi kan se hva som skjer ved å hakke opp det feide området som følger:
fordi målehjulet er i midten av armen, når armen roterer, klemmer den de små blokkene på den ene siden som den utvider dem på den andre. Disse effektene avbryter hverandre nøyaktig.
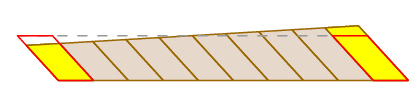
en helt streng bevis kan gis ved å bruke formelen for endring av variabler i en dobbel integral og uttrykket for hjulet reise som en bane integrert.
anta nå at hjulet er plassert et annet sted. Si at posisjonen er c + v hvor c er midten av armen, og v en vektor langs armen. Lengden på v vil forbli fast, si ved ρ. Banen som hjulet følger er c (t) + v (t). Baneintegralet er nå
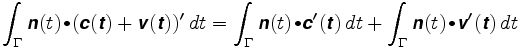
det første integralet er avstanden hjulet ville reise hvis det var i midten av armen. I det andre er vektoren v (t) alltid vinkelrett på n, og v (t) har konstant lengde. Vektoren v (t) beveger seg rundt på en sirkel av radius lik ρ. Derfor er prikkproduktet av n og v'(t) bare den signerte lengden av v'(t), og det andre integralet er lik den totale rotasjonen av armen. Derfor:
hvis hjulet er i avstand ρ fra armens midtpunkt, er avstanden C hjulmålene C0, avstanden som ville bli målt hvis hjulet var i midten, pluss ρ ganger den totale vinkelen θ som armen roterer.
du kan umiddelbart se et enkelt tilfelle av dette ved å rotere armen rundt senteret. Ved å kombinere Dette Med Guldins Teorem ser vi at i alle tilfeller:
C = C0 + ρ θ
Område Feiet ut = l c0 = l c – l ρ θ
det fulle Resultatet
guldins Formel gir et signert område – hvis du feier bakover over et område, går hjulet bakover og du avbryter området du allerede har dekket. Hvis vi bruker dette til saken der friarmen kommer tilbake nøyaktig til hvor den startet, ser vi at lC er lik arealet av den lukkede regionen sporet ut av høyre ende av armen minus den av regionen som er feid ut av den venstre.
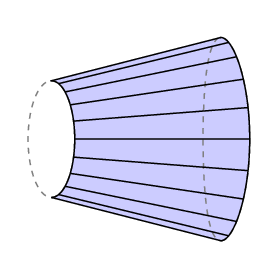
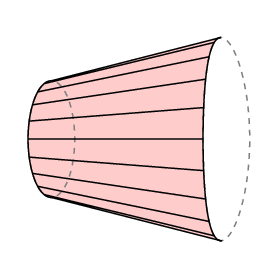
sporet av sporeren. Videre ligger normalt stangen utenfor regionen som skal måles, og i dette tilfellet må den totale rotasjonsmengden av armen være 0. Så i dette tilfellet har vi
Område av regionen spores = lC
Her er figuren Inkludert Av Jakob Amsler, oppfinneren, i sin opprinnelige papir på instrumentet han oppfant:
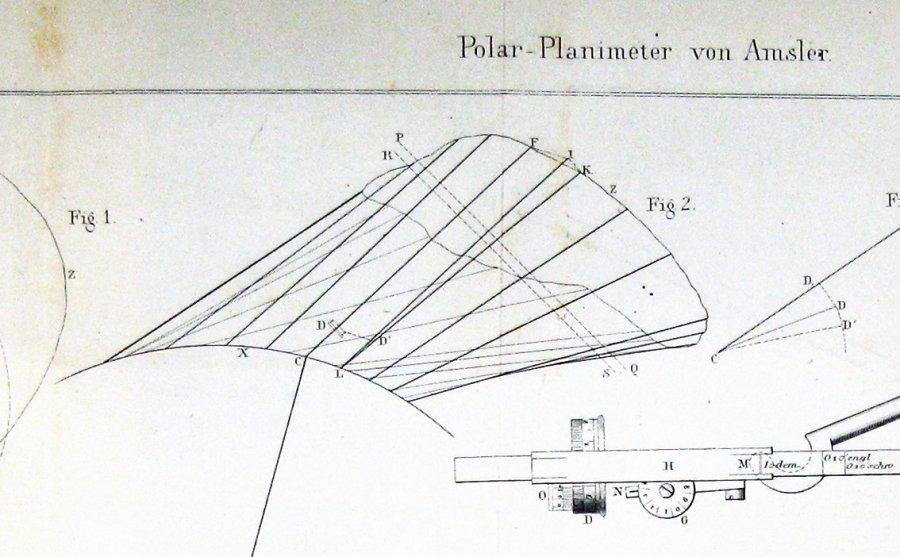
Det virker ganske klart fra dette At Amsler avledet sin konstruksjon gjennom Noen form For Guldins teorem.
Planimetre og Greens Teorem
som vi allerede har nevnt, har vi valgt orienteringen til planimeteret, planimeterkonfigurasjonen er en kontinuerlig funksjon av sporposisjonen. Si at vi velger den positive orienteringen. Da kan vi feste til hvert punkt i ringrommet en enhetsvektor n, den som peker mot urviseren og vinkelrett på sporarmen på sporeren.
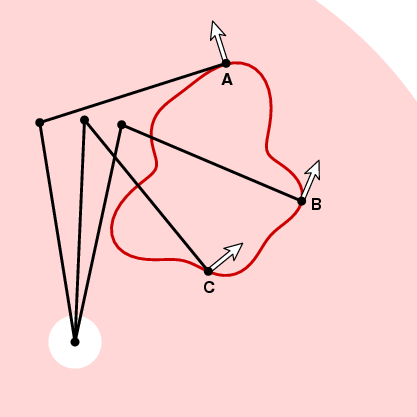
Hvordan målehjulet skal reagere på bevegelse langs kurven i neste øyeblikk, avhenger av vinkelen mellom denne vektoren og kurvens tangentvektor. På A i bildet ovenfor vil målehjulet ikke bevege seg fordi bevegelsen langs kurven er parallell med sporarmen. Ved B hvis sporeren beveger seg en liten avstand ds, så vil målehjulet. Og Ved C vil målehjulet bevege seg en viss avstand mellom 0 og ds. For å være presis, anta at t er enheten tangent vektor på et tidspunkt av kurven. Hvis tracer flytter avstand ds langs kurven, på det punktet målehjulet vil flytte en avstand d ds, der d = n . t, punktproduktet til enhetsvektorene t og n. Med andre ord, hvis vi beveger oss rundt kurven Γ, vil målehjulet flytte en total avstand lik integralet av n . t ds (dot product), eller
Men siden hvert punkt i ringrommet tilsvarer en unik positiv konfigurasjon av planimeteret, kan vi tildele en vektor n til hvert indre punkt i ringrommet, og det definerer derfor et vektorfelt. Kurven Hryvnias er grensen til dens indre Hryvnias, og etter en av våre forutsetninger er dette inneholdt helt i regionen der n er definert. Greens Teorem forteller oss at stiintegralet rundt grensen til denne regionen også er lik et bestemt integral over Ω: Derfor
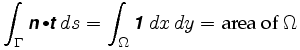
Mer presist, Greens Teorem forteller oss at
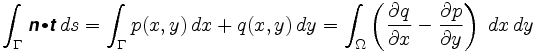
hvor n = er vektorfeltet involvert. Integranden i det dobbelte integralet kalles krøllen til vektorfeltet.
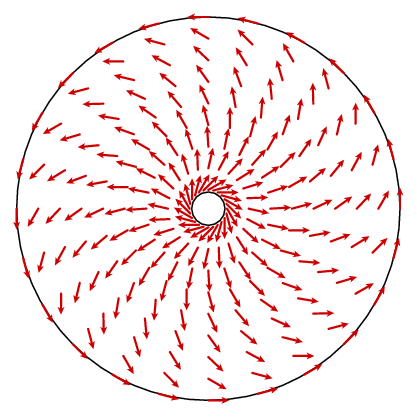
Dette ser ikke ut til å få oss veldig langt. Det som burde skje er at krøllen er en konstant 1. I prinsippet kan vi finne en formel for vektorfeltet n og beregne krøllen, men det er ikke veldig opplysende. Vi kan imidlertid dra nytte av et annet faktum. Vektorfeltet har sirkulær symmetri, noe som betyr at det bestemmes av hva det er på en radius. Cosinus loven gir oss en enkel formel for omkretskomponenten.
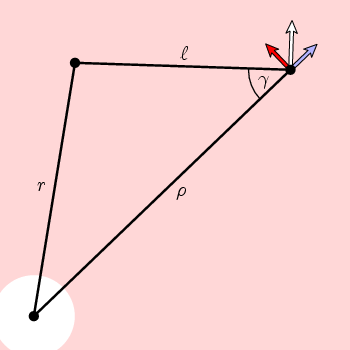
det følger av enkel geometri i denne figuren at omkretskomponenten til n er
f(ρ) = cos(γ) = (ρ 2 + l 2 – r 2)/(2 ρ l)
Det virkelige poenget Med Greens Teorem er at For å verifisere at integranden er 1, er det nok å verifisere at banen er integrert rundt passende små stier er det samme som området. For dette velger vi våre regioner å være som her:
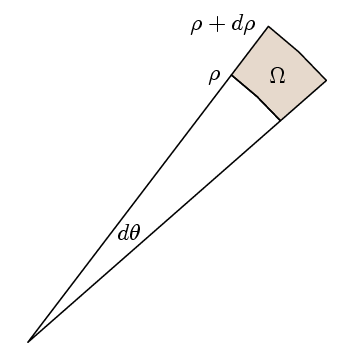
Deretter l ganger banen er integrert
l (ρ+dp)( f(ρ+dp)- f(ρ) ) dθ
eller
(θ/2) ( (ρ + dp) 2 – ρ 2)
som er området i regionen Ω.Guldins Teorem innebærer at bevegelsen til et målehjul vil fortelle deg området sporet ut av sporeren når armen med et målehjul på det sporer ut en kurve, men har en ende begrenset til en endimensjonal kurve. Dette skjer for eksempel med rullende planimeter, hvor pivoten er begrenset til en rett linje ved å være på en rullende sylinder.
for å finne ut mer
-
lager og selger fortsatt planimetre. - Differensial Og Integral Kalkulus Volum II, R. Courant, Blackie & Sønn, 1936. Seksjonen Om Guldins Formel (s. 294-298) gir en forklaring på hvordan planimeteret fungerer.Amslers opprinnelige artikkel, Vierteljahresschrift Der Naturforschenden Gesellschaft I Zuerich, 1856. Dette mangler diagrammene, Men De er her:
- Amslers første diagram
- Amslers andre diagram
Vår takk Til Donna Sammis fra Stony Brook University Library for å finne artikkelen og til ektemannen Robert for å levere fotografier av figurene.Selskapet Som Amsler grunnla produserte instrumenter godt inn i det 20. århundre. Dette bildet viser logoen, på en pantograf versjon av planimeter:
- «Om Planimeter,» EngineerSupply. Selskapet har også lagt ut en video På YouTube.
Bill Casselman
Universitetet I British Columbia, Vancouver,Canada
cass at math.ubc.ca
John Eggers
Universitetet I California, San Diego
jeggers at ucsd.edu
De SOM har TILGANG TIL JSTOR kan finne noen av papirene nevnt ovenfor der. For de med tilgang, Kan American Mathematical Society MathSciNet brukes til å få ekstra bibliografisk informasjon og vurderinger av noen av disse materialene. Noen av elementene ovenfor kan nås via ACM Portal, som også gir bibliografiske tjenester.