Introduksjon
Principal Components Analysis (PCA) er en dimensjonsreduksjonsalgoritme som kan brukes til å øke hastigheten på din unsupervised feature learning algorithm. Enda viktigere, forståelse AV PCA vil gjøre det mulig for oss å senere implementere bleking, noe som er et viktig forbehandlingstrinn for mange algoritmer.
Anta at du trener algoritmen din på bilder. Da vil inngangen være noe overflødig, fordi verdiene til tilstøtende piksler i et bilde er svært korrelerte. Konkret, anta at vi trener på 16×16 gråtonebilder. Da \textstyle x \ in \ re^{256} er 256 dimensjonsvektorer, med en funksjon \textstyle x_j som svarer til intensiteten til hver piksel. På grunn AV korrelasjonen mellom tilstøtende piksler, VIL PCA tillate oss å tilnærme inngangen med en mye lavere dimensjonal, mens det oppstår svært liten feil.
Eksempel og Matematisk Bakgrunn
for vårt løpende eksempel vil vi bruke et datasett \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} med \textstyle n=2 dimensjonale innganger, slik at \textstyle x^{(i)} \i \Re^2. Anta at vi vil redusere dataene fra 2 dimensjoner til 1. (I praksis vil vi kanskje redusere data fra 256 til 50 dimensjoner, si; men ved å bruke lavere dimensjonsdata i vårt eksempel kan vi visualisere algoritmene bedre.) Her er datasettet vårt:
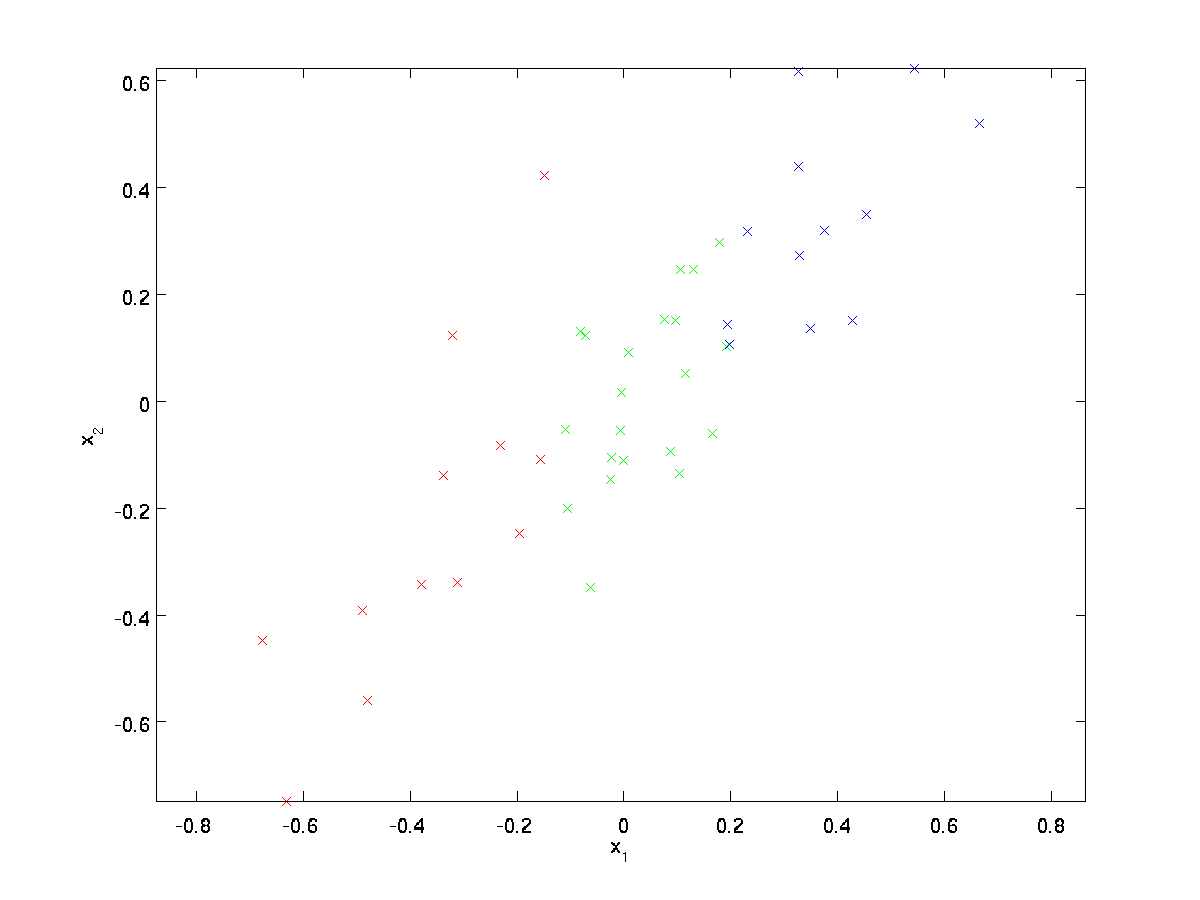
Disse dataene er allerede forhåndsbehandlet slik at hver av funksjonene \ textstyle x_1 og \ textstyle x_2 har omtrent samme gjennomsnitt (null) og varians.
for illustrasjonens formål har vi også farget hvert av punktene en av tre farger, avhengig av deres \textstyle x_1-verdi; disse fargene brukes ikke av algoritmen, og er kun til illustrasjon.
PCA vil finne et lavere dimensjonalt underrom til å projisere våre data.
fra visuelt å undersøke dataene, ser det ut til at \textstyle u_1 er den viktigste variasjonsretningen for dataene, og \textstyle u_2 den sekundære variasjonsretningen:
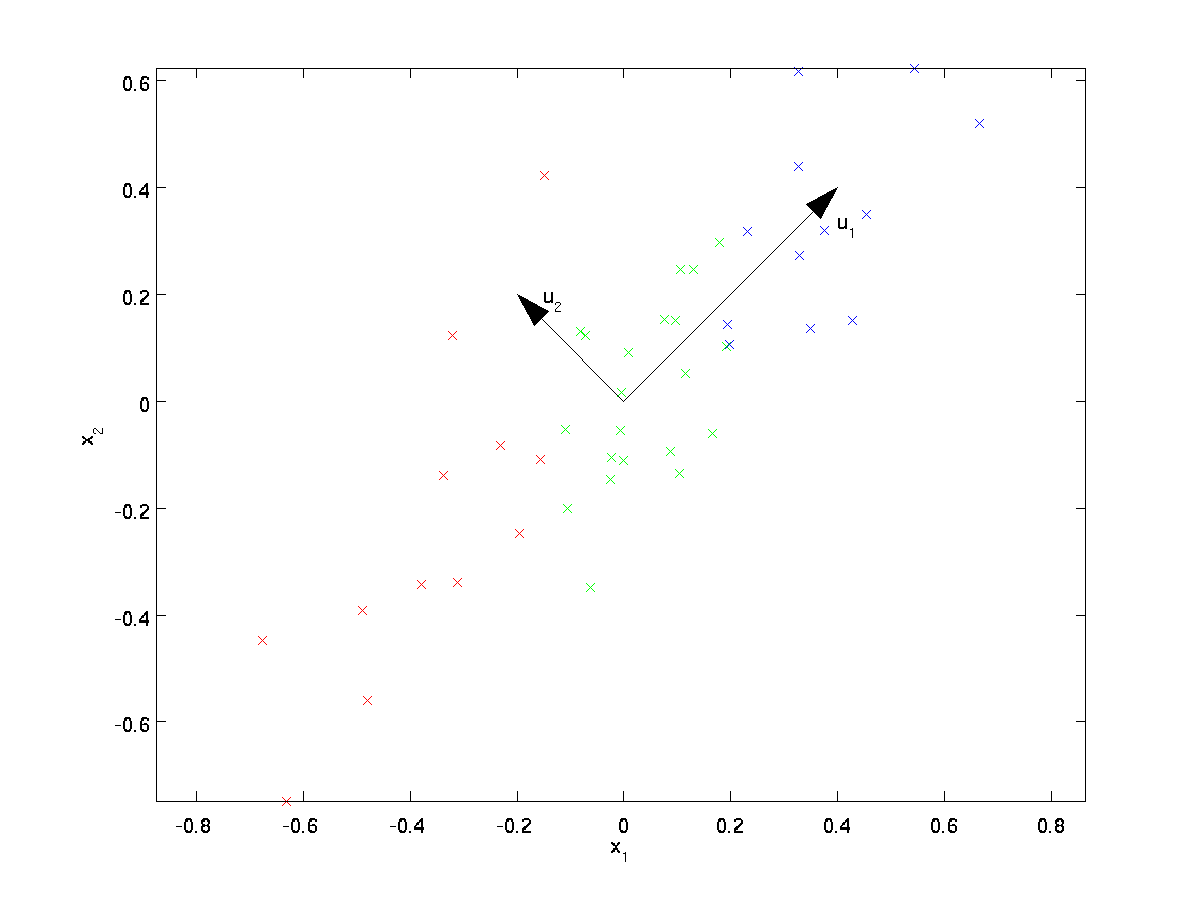
Dvs. dataene varierer mye mer i retningen \textstyle u_1 enn \textstyle u_2. For mer formelt å finne retningene \textstyle u_1 og \textstyle u_2, beregner vi først matrisen \textstyle \ Sigma som følger:
\begin{align} \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \ end{align}
hvis \textstyle x har null gjennomsnitt, er \textstyle \ Sigma nøyaktig kovariansmatrisen til \ textstyle x. (symbolet «\textstyle \Sigma», uttalt «Sigma», er standardnotasjonen for å betegne kovariansmatrisen. Dessverre ser det ut som summeringssymbolet, som i \sum_{i=1}^n i; men disse er to forskjellige ting.)
det kan da bli vist at \ textstyle u_1—den viktigste variasjonsretningen til dataene-er den øverste (viktigste) egenvektoren til \ textstyle \ Sigma, og \textstyle u_2 er den andre egenvektoren.
Merk: hvis du er interessert i å se en mer formell matematisk avledning/begrunnelse av dette resultatet, se CS229 (Maskinlæring) forelesningsnotater PÅ PCA (lenke nederst på denne siden). Du trenger ikke å gjøre det for å følge dette kurset, men.
du kan bruke standard numerisk lineær algebra programvare for å finne disse egenvektorer (se Implementerings Notater). Konkret, la oss beregne egenvektorer av \ textstyle \ Sigma, og stable egenvektorer i kolonner for å danne matrisen \textstyle U:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.
vektorene \textstyle u_1 og \textstyle u_2 i vårt eksempel danner et nytt grunnlag der vi kan representere dataene. Konkret, la \textstyle x \ i \ Re^2 være noe treningseksempel. Da \textstyle u_1 ^ Tx er lengden (størrelsen) av projeksjonen av \textstyle x på vektoren \textstyle u_1.
på Samme måte er \textstyle u_2 ^ Tx størrelsen på \ textstyle x projisert på vektoren \textstyle u_2.
Rotere Dataene
dermed kan vi representere \textstyle x i \textstyle (u_1, u_2)-basis ved å beregne
\begin{align}x_{\rm rot} = U^Tx = \begin{Bmatrix} u_1^Tx \\ U_2^Tx \end{bmatrix} \end{align}
(subscriptet » rot » kommer fra observasjonen at dette tilsvarer en rotasjon (og muligens refleksjon) av opprinnelige data.) La oss ta hele treningssettet, og beregne \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)} for hver \ textstyle jeg.:

dette er treningssettet rotert inn i\textstyle u_1, \ textstyle u_2 basis. I det generelle tilfellet vil \textstyle U^Tx være treningssettet rotert inn i basis\textstyle u_1, \textstyle u_2,…, \textstyle u_n.
en av egenskapene til \ textstyle U er at den er en» ortogonal » matrise, som betyr at den tilfredsstiller \textstyle U^TU = UU^T = I. Så hvis du noen gang trenger å gå fra de roterte vektorene \textstyle x_{\rm rot} tilbake til den opprinnelige data \textstyle x, kan du beregne
\begin{align}x = U x_{\rm rot} ,\end{align}
fordi \textstyle U X_{\rm rot} = UU^t x = x.
Redusere Datadimensjonen
vi ser at hovedretningen for variasjonen av dataene er den første dimensjonen \textstyle x_{\rm rot,1} av disse roterte dataene. Således, hvis vi vil redusere disse dataene til en dimensjon, kan vi sette
\begin{align}\tilde{x}^{(i)} = x_ {\rm rot, 1}^{(i)} = u_1^Tx^{(i)} \in \Re.\end{align}
mer generelt, hvis \textstyle x \i \Re^n og vi ønsker å redusere den til en \textstyle k dimensjonal representasjon \textstyle \tilde{x} \i \re^k (hvor k < n), ville vi ta de første \textstyle k komponentene i\textstyle x_ {\rm rot}, som tilsvarer de øverste \ textstyle k variasjonsretningene.
En annen måte Å forklare PCA på er at \textstyle x_{\rm rot} er en \textstyle n dimensjonsvektor, hvor de første komponentene sannsynligvis er store (f. eks., i vårt eksempel så vi at \textstyle x_{\rm rot, 1}^{(i)} = u_1^Tx^{(i)} tar rimelig store verdier for de fleste eksempler \textstyle i), og de senere komponentene er sannsynligvis små (for eksempel i vårt eksempel, \textstyle x_{\rm rot, 2}^{(i)} = u_2^Tx^{(i)} var mer sannsynlig å være små). Hva PCA gjør det, faller de senere (mindre) komponentene av \ textstyle x_{\rm rot}, og tilnærmer dem bare med 0. Konkret kan vår definisjon av \textstyle \tilde{x} også ankommet ved å bruke en tilnærming til \textstyle x_{\rm rot} hvor alle, men de første \textstyle k-komponentene er nuller. Med andre ord har vi:
\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rot, 1} \\\vdots \\ x_{\rm rot,k} \\0 \ \ vdots \ \ 0 \ \ \ end{bmatrix} \ca\begin{bmatrix} x_ {\rm rot,1}\\\vdots \ \ x_ {\rm rot,k}\\x_ {\rm rot,k}\\x_ {\rm rot,k} \ \ x_ {\rm rot,k+1}\\\vdots \\x_ {\rm rot, n} \end{bmatrix}= x_ {\rm rot} \ end {align}
i vårt eksempel gir dette oss følgende plott av \ textstyle \ tilde {x} (ved hjelp av \ textstyle n=2, k=1):

siden de endelige \ textstyle nk-komponentene i \ textstyle \tilde{x} som definert ovenfor alltid vil være null, er det ikke nødvendig å holde disse nullene rundt, og så definerer vi \ textstyle \tilde{x} som en \textstyle k-dimensjonal vektor med bare de første \ textstyle k (ikke-null) komponentene.
dette forklarer også hvorfor vi ønsket å uttrykke dataene våre i \textstyle u_1, u_2, \ldots, u_n basis: Å Bestemme hvilke komponenter som skal beholdes, blir bare å holde de øverste \ textstyle k-komponentene. Når vi gjør dette, sier vi også at vi » beholder top \ textstyle k PCA (eller principal) komponenter.»
Gjenopprette En Tilnærming Av Dataene
nå er \textstyle \tilde{x} \i \Re^k en lavere dimensjonal, «komprimert» representasjon av den opprinnelige \textstyle x \i \re^n. Gitt \textstyle \tilde{x}, Hvordan kan vi gjenopprette en tilnærming \textstyle \hat{x} til den opprinnelige verdien av \ textstyle x? Fra en tidligere seksjon vet vi at \textstyle x = U x_{\rm rot}. Videre kan vi tenke på \ textstyle \tilde {x} som en tilnærming til \ textstyle x_{\rm rot}, hvor vi har satt de siste \ textstyle nk-komponentene til nuller. Derfor, gitt \textstyle \tilde{x} \i \Re^k, kan vi pad det ut med \textstyle nk nuller for å få vår tilnærming til \textstyle x_{\rm rot} \I \re^n. Til Slutt pre-multipliser vi med \textstyle U for å få vår tilnærming til \textstyle x. Konkret får vi
\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}_1 \ \ vdots \ \ \ tilde{x}_k \ \ 0 \ \ vdots\ \0 \ end{bmatrix} = \ sum_{i=1}^k u_i \tilde{x}_i. \end{align}
den endelige likestillingen ovenfor kommer fra definisjonen av \textstyle U gitt tidligere. (I en praktisk implementering ville vi faktisk ikke nullpute \textstyle \Tilde {x} og deretter multiplisere med \ textstyle U, siden det ville bety å multiplisere mange ting med nuller; i stedet ville vi bare multiplisere \textstyle \tilde {x} \i \ re^k med de første \ textstyle k kolonnene av \ textstyle U som i det endelige uttrykket ovenfor.) Ved å bruke dette på datasettet får vi følgende plott for \ textstyle \ hat{x}:
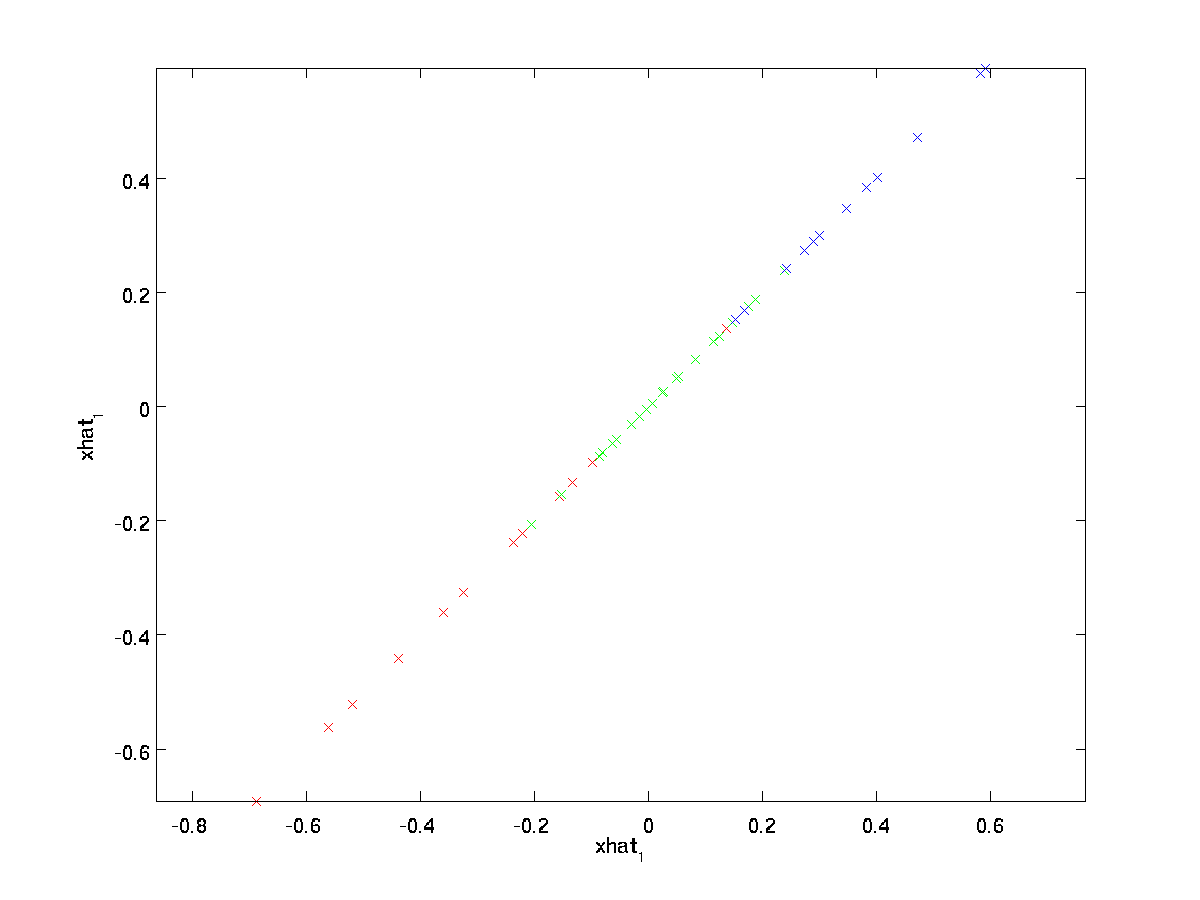
Vi bruker dermed en 1-dimensjonal tilnærming til det opprinnelige datasettet.
hvis du trener en autoencoder eller annen unsupervised funksjon læring algoritme, vil kjøretiden for algoritmen avhenger av dimensjonen av inngangen. Hvis du mater \textstyle \ tilde{x} \ i \ re^k inn i læringsalgoritmen din i stedet for \ textstyle x, vil du trene på en lavere dimensjonal inngang, og dermed kan algoritmen din kjøre betydelig raskere. For mange datasett kan den nedre dimensjonale \textstyle \ tilde{x} representasjonen være en ekstremt god tilnærming til originalen, og bruk AV PCA på denne måten kan øke hastigheten på algoritmen din mens du introduserer svært liten tilnærmingsfeil.
Antall komponenter som skal beholdes
Hvordan setter vi \textstyle k; dvs. hvor MANGE pca-komponenter skal vi beholde? I vårt enkle 2-dimensjonale eksempel virket det naturlig å beholde 1 ut av 2-komponentene, men for høyere dimensjonsdata er denne beslutningen mindre trivial. Hvis \textstyle k er for stor, vil vi ikke komprimere dataene mye; i grensen til \textstyle k=n, bruker vi bare de opprinnelige dataene (men roteres til et annet grunnlag). Omvendt, hvis \textstyle k er for liten, kan vi bruke en veldig dårlig tilnærming til dataene.for å bestemme hvordan man setter \textstyle k, vil vi vanligvis se på «‘prosent av variansen beholdt «‘ for forskjellige verdier av \ textstyle k. Konkret, Hvis \textstyle k=n, så har vi en nøyaktig tilnærming til dataene, og vi sier at 100% av variansen beholdes. Dvs., all variasjon av de opprinnelige dataene beholdes. Omvendt, hvis \textstyle k = 0, så tilnærmer vi alle dataene med nullvektoren, og dermed beholdes 0% av variansen.
Mer generelt, la \textstyle \ lambda_1, \lambda_2, \ldots, \lambda_n være egenverdiene til \textstyle \Sigma (sortert i avtagende rekkefølge), slik at \ textstyle \ lambda_j er egenverdien som svarer til egenvektoren \textstyle u_j.:
\start{align} \ frac {\sum_{j = 1}^k \ lambda_j} {\sum_{j = 1}^n \ lambda_j}.\end{align}
i vårt enkle 2d-eksempel ovenfor, \textstyle \lambda_1 = 7.29, og \textstyle \lambda_2 = 0.69. Således, ved å holde bare \textstyle k=1 hovedkomponenter, beholdt vi \textstyle 7.29/(7.29+0.69) = 0.913, eller 91,3% av variansen.
en mer formell definisjon av prosentvis varians beholdt er utenfor omfanget av disse notene. Det er imidlertid mulig å vise at \textstyle \lambda_j =\sum_{i=1}^m x_ {\rm rot, j}^2. Således, hvis \textstyle \lambda_j \ca 0, viser det at \textstyle x_{\rm rot, j} vanligvis er nær 0 uansett, og vi mister relativt lite ved å tilnærme det med en konstant 0. Dette forklarer også hvorfor vi beholder de øverste hovedkomponentene (tilsvarende de større verdiene av \textstyle \lambda_j) i stedet for de nederste. De øverste hovedkomponentene \ textstyle x_{\rm rot, j} er de som er mer variable og som tar større verdier, og som vi ville pådra oss en større tilnærmingsfeil hvis vi skulle sette dem til null.
i tilfelle av bilder er en vanlig heuristisk å velge \textstyle k for å beholde 99% av variansen. Med andre ord velger vi den minste verdien av \ textstyle k som tilfredsstiller
\begin{align}\frac {\sum_{j = 1}^k \ lambda_j} {\sum_{j = 1}^n \ lambda_j} \ geq 0.99. \end{align}
avhengig av programmet, hvis du er villig til å pådra seg noen ekstra feil, brukes også verdier i 90-98% – området noen ganger. Når du beskriver for andre HVORDAN DU brukte PCA, sier at du valgte \ textstyle k for å beholde 95% av variansen, vil det også være en mye lettere tolkbar beskrivelse enn å si at du beholdt 120 (eller hva som helst annet antall) komponenter.
Pca På Bilder
FOR AT PCA skal fungere, vil vi vanligvis at hver av funksjonene \textstyle x_1, x_2, \ ldots, x_n skal ha et lignende utvalg av verdier til de andre (og å ha et middel nær null). Hvis DU har brukt PCA på andre applikasjoner før, kan du derfor ha forhåndsbehandlet hver funksjon separat for å ha null gjennomsnitt og enhetsvarians, ved å estimere gjennomsnittet og variansen for hver funksjon \textstyle x_j. dette er Imidlertid ikke forbehandlingen som vi vil gjelde for de fleste typer bilder. Spesifikt, anta at vi trener vår algoritme på «‘naturlige bilder»‘, slik at \textstyle x_j er verdien av pixel \ textstyle j. med» naturlige bilder » betyr vi uformelt typen bilde som et typisk dyr eller en person kan se over deres levetid.
Merk: Vanligvis bruker vi bilder av utendørs scener med gress, trær, etc., og kutte ut små (si 16×16) bildeplaster tilfeldig fra disse for å trene algoritmen. Men i praksis er de fleste læringsalgoritmer ekstremt robuste for den eksakte typen bilde det er trent på, så de fleste bilder tatt med et vanlig kamera, så lenge de ikke er for uklare eller har merkelige gjenstander, skal fungere.
når du trener på naturlige bilder, er det lite fornuftig å estimere et eget middel og varians for hver piksel, fordi statistikken i en del av bildet skal (teoretisk) være den samme som alle andre.
denne egenskapen av bilder kalles «‘ stasjonaritet.»‘
i detalj, for AT PCA skal fungere godt, krever vi uformelt at (i) funksjonene har omtrent null gjennomsnitt, og (ii) de forskjellige funksjonene har lignende avvik til hverandre. Med naturlige bilder, (ii) er allerede fornøyd selv uten varians normalisering, og så vil vi ikke utføre noen varians normalisering.(hvis du trener på lyddata-si, på spektrogrammer – eller på tekstdata—si, bag-of-word vektorer – vil vi vanligvis ikke utføre varians normalisering heller.)
FAKTISK ER PCA invariant til skaleringen av dataene, og vil returnere de samme egenvektorer uavhengig av skaleringen av inngangen. Mer formelt, hvis du multipliserer hver funksjonsvektor \textstyle x med noe positivt tall (dermed skalerer hver funksjon i hvert treningseksempel med samme nummer), VIL PCAS egenvektorer ikke endres.
Så, vi vil ikke bruke varians normalisering. Den eneste normaliseringen vi trenger å utføre, er gjennomsnittlig normalisering, for å sikre at funksjonene har et middel rundt null. Avhengig av søknaden, er vi ofte ikke interessert i hvor lyst det generelle inngangsbildet er. I objektgjenkjenningsoppgaver påvirker for eksempel ikke den generelle lysstyrken i bildet hvilke objekter det er i bildet. Mer formelt er vi ikke interessert i den gjennomsnittlige intensitetsverdien til en bildepatch; dermed kan vi trekke ut denne verdien, som en form for gjennomsnittlig normalisering.
Konkret, hvis \textstyle x^{(i)} \i \ Re^{n} er (gråtoner) intensitetsverdiene til en 16×16 bildeplaster (\textstyle n = 256), kan vi normalisere intensiteten til hvert bilde \ textstyle x^{(i)} som følger:
\mu^{(i)} := \frac{1}{n} \ sum_{j=1}^n x^{(i)}_jx^{(i)} _j := x^{(i)} _j – \mu^{(i)}
For alle \ textstyle j
Merk at de to trinnene ovenfor er gjort separat for hvert bilde \textstyle x^{(i)}, og at \textstyle \mu^{(i)} her er den gjennomsnittlige intensiteten til bildet \ textstyle x^{(i)}. Spesielt er dette ikke det samme som å estimere en middelverdi separat for hver piksel \textstyle x_j.
hvis du trener algoritmen din på andre bilder enn naturlige bilder (for eksempel bilder av håndskrevne tegn eller bilder av enkelt isolerte objekter sentrert mot en hvit bakgrunn), kan andre typer normalisering være verdt å vurdere, og det beste valget kan være applikasjonsavhengig. Men når du trener på naturlige bilder, vil det være en rimelig standard å bruke per-image-normaliseringsmetoden som gitt i ligningene ovenfor.
Whitening
VI har brukt PCA for å redusere dimensjonen av dataene. Det er et nært beslektet preprocessing trinn kalt whitening (eller, i noen andre litteratur, sphering) som er nødvendig for noen algoritmer. Hvis vi trener på bilder, er raw-inngangen overflødig, siden tilstøtende pikselverdier er svært korrelerte. Målet med whitening er å gjøre input mindre overflødig; mer formelt, vår desiderata er at våre læringsalgoritmer ser en trening innspill der (i) funksjonene er mindre korrelert med hverandre, og (ii) funksjonene alle har samme varians.
2d eksempel
vi vil først beskrive bleking ved hjelp av vårt tidligere 2d-eksempel. Vi vil da beskrive hvordan dette kan kombineres med utjevning, og til slutt hvordan å kombinere dette MED PCA.
Hvordan kan vi gjøre våre innspill funksjoner ukorrelert med hverandre? Vi hadde allerede gjort dette når computing \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}.
Gjenta vår forrige figur, vår tomt for \textstyle x_{\rm rot} var:

kovariansmatrisen til disse dataene er gitt av:
\begin{align}\begin{bmatrix}7.29&& 0.69\end{bmatrix}.\end{align}
(Merk: Teknisk sett vil mange av uttalelsene i denne delen om «kovariansen» bare være sanne hvis dataene har null gjennomsnitt. I resten av denne delen vil vi ta denne antakelsen som implisitt i våre uttalelser. Men selv om dataens gjennomsnitt ikke er akkurat null, er intuisjonene vi presenterer her fortsatt sanne, og så er dette ikke noe du bør bekymre deg for.)
det er ingen tilfeldighet at diagonalverdiene er \textstyle \lambda_1 og \textstyle \lambda_2. Videre er de diagonale oppføringene null; dermed er \textstyle x_{\rm rot, 1} og \ textstyle x_{\rm rot, 2} ukorrelert, og tilfredsstiller en av våre desiderata for hvite data (at funksjonene er mindre korrelerte).
for å gjøre hver av våre inngangsfunksjoner har enhetsvarians, kan vi bare rescale hver funksjon \textstyle x_{\rm rot, i} av \ textstyle 1 / \sqrt{\lambda_i}. Konkret definerer vi våre hvite data \ textstyle x_{\rm PCAwhite} \i \ re^n som følger:
\begin{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}}. \ end{align}
Plotting \ textstyle x_{\Rm PCAwhite}, får vi:

Disse dataene har nå kovarians lik identitetsmatrisen \ textstyle I. Vi sier at \textstyle x_{\Rm PCAwhite} er VÅR pca-hvite versjon av dataene: de forskjellige komponentene i \ textstyle x_{\rm PCAwhite} er ukorrelerte og har enhetsvarians.
Bleking kombinert med dimensjonsreduksjon. Hvis du vil ha data som er hvite og som er lavere dimensjonale enn den opprinnelige inngangen, kan du også eventuelt bare beholde de øverste \ textstyle k-komponentene i \ textstyle x_{\Rm PCAwhite}. Når VI kombinerer PCA-bleking med regularisering (beskrevet senere), vil de siste komponentene i \textstyle x_{\rm PCAwhite} være nesten null uansett, og dermed kan trygt slippes.
ZCA Whitening
Til Slutt viser det seg at denne måten å få dataene til å ha kovariansidentitet \ textstyle I er ikke unik. Konkret, hvis \textstyle R er en ortogonal matrise, slik at den tilfredsstiller \ textstyle RR^T = R^TR = i (mindre formelt, hvis \ textstyle R er en rotasjon / refleksjonsmatrise), vil \textstyle R\, x_{\Rm PCAwhite} også ha identitetskovarians.
i zca whitening velger vi \textstyle R = U. vi definerer
\begin{align}x_{\rm ZCAwhite} = U x_{\rm PCAwhite}\end{align}
Plotting \textstyle x_{\rm ZCAwhite}, vi får:

det kan vises det ut av alle mulige valg For \TEXTSTYLE r, forårsaker dette rotasjonsvalget \Textstyle X_{\rm zcawhite} å være så nært Som mulig Til De Opprinnelige Inngangsdataene \Textstyle x.
når vi bruker zca whitening (i motsetning til pca whitening), beholder vi vanligvis alle \textstyle n dimensjoner Av Dataene, Og prøver ikke å redusere dimensjonen.
Regularizaton
når man implementerer pca whitening eller ZCA whitening i praksis, vil noen ganger noen av egenverdiene \textstyle \lambda_i være numerisk nær 0, og dermed vil skaleringstrinnet der vi deler med \sqrt{\lambda_i} innebære å dele med en verdi nær null; dette kan føre til at dataene blåser opp (ta på store verdier) eller på annen måte være numerisk ustabile. I praksis implementerer vi derfor dette skaleringstrinnet ved hjelp av en liten mengde regularisering, og legger til en liten konstant \textstyle \epsilon til egenverdiene før du tar kvadratroten og invers:
start{align}x_ {\Rm PCAwhite, i} = \ frac{x_{\rm rot, i} } {\sqrt {\lambda_i + \ epsilon}}.\end{align}
når \textstyle x tar verdier rundt \ textstyle, kan en verdi av \textstyle \ epsilon \ ca 10^{-5} være typisk.
for tilfelle av bilder, legger \textstyle \ epsilon her også effekten av litt utjevning (eller lavpassfiltrering) inngangsbildet. Dette har også en ønskelig effekt av å fjerne aliasing artefakter forårsaket av måten piksler er lagt ut i et bilde ,og kan forbedre funksjonene lært (detaljer er utenfor omfanget av disse notatene).
ZCA whitening ER en form for forbehandling av dataene som kartlegger den fra \ textstyle x til \ textstyle x_{\rm ZCAwhite}. Det viser seg at dette også er en grov modell av hvordan det biologiske øyet (netthinnen) behandler bilder. Spesielt, som øyet oppfatter bilder, vil de fleste tilstøtende «piksler» i øyet oppleve svært like verdier, siden tilstøtende deler av et bilde har en tendens til å være svært korrelert i intensitet. Det er derfor sløsing for øyet å måtte overføre hver piksel separat (via din optiske nerve) til hjernen din. I stedet utfører retina en decorrelation-operasjon (dette gjøres via retinale nevroner som beregner en funksjon kalt «på senter, av surround / off center, på surround») som ligner DEN som utføres AV ZCA. Dette resulterer i en mindre overflødig representasjon av inngangsbildet, som deretter overføres til hjernen din.
Implementere PCA Whitening
i denne delen oppsummerer VI PCA, PCA whitening og ZCA whitening algoritmer, og beskriver også hvordan du kan implementere dem ved hjelp av effektive lineære algebra biblioteker.
Først må vi sørge for at dataene har (omtrent) null-middel. For naturlige bilder oppnår vi dette (omtrent) ved å trekke middelverdien til hver bildepatch.
vi oppnår dette ved å beregne gjennomsnittet for hvert plaster og trekke det fra for hvert plaster. I Matlab kan vi gjøre dette ved å bruke
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);Deretter må Vi beregne \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^M (x^{(i)})(x^{(i)})^T. Hvis du implementerer dette I Matlab (eller selv om du implementerer dette I C++, Java, etc., men har tilgang til et effektivt lineært algebrabibliotek), gjør det som en eksplisitt sum er ineffektiv. I stedet kan vi beregne dette i et fall som
sigma = x * x' / size(x, 2);(Sjekk matematikken selv for korrekthet.) Her antar vi at x er en datastruktur som inneholder ett treningseksempel per kolonne (så x er en \textstyle n-by – \ textstyle m matrise).
NESTE beregner PCA egenvektorer av \Sigma. Man kan gjøre dette ved Hjelp Av Matlab eig-funksjonen. Men fordi \Sigma er en symmetrisk positiv semi-definite matrise, er det mer numerisk pålitelig å gjøre dette ved hjelp av svd-funksjonen. Konkret, hvis du implementerer
= svd(sigma);vil matrisen U inneholde egenvektorer av \Sigma (en egenvektor per kolonne, sortert i rekkefølge fra topp til bunn egenvektor), og de diagonale oppføringene i matrisen S vil inneholde de tilsvarende egenverdiene (også sortert i avtagende rekkefølge). Matrisen V vil være lik U, og kan trygt ignoreres.
(Merk: Svd-funksjonen beregner faktisk singulære vektorer og singulære verdier av en matrise, som for det spesielle tilfellet av en symmetrisk positiv semi-definite matrise—som er alt vi er opptatt av her-er lik sin egenvektorer og egenverdier. En full diskusjon av singulære vektorer vs egenvektorer er utenfor omfanget av disse notatene.)
til Slutt kan du beregne \textstyle x_{\rm rot} og \textstyle \tilde{x} som følger:
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keepdette gir DIN pca-representasjon av dataene i form av \textstyle \tilde{x} \ i \ re^k. Forresten, hvis x er en \textstyle n-by-\textstyle m matrise som inneholder alle treningsdataene dine, er dette en vektorisert implementering, og uttrykkene ovenfor fungerer også for å beregne x_{\rm rot} og \tilde{x} for hele treningssettet alt på en gang. Den resulterende x_{\rm rot} og \tilde{x} vil ha en kolonne som svarer til hvert treningseksempel.
for å beregne PCA-hvite data \textstyle x_{\Rm PCAwhite}, bruk
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;Siden S diagonal inneholder egenverdiene \textstyle \lambda_i, viser dette seg å være en kompakt måte å beregne \textstyle x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}} samtidig for alle \Textstyle i.
til slutt kan du også beregne zca-hvite data \textstyle x_{\rm zcawhite} som:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;