The Franck-Condon Principle describes the intensities of vibronic transitions, or the absorption or emission of a photon. Ela afirma que quando uma molécula está passando por uma transição eletrônica, como a ionização, a configuração nuclear da molécula não experimenta nenhuma mudança significativa. Isto é devido de fato que os núcleos são muito mais massivos do que os elétrons e a transição eletrônica ocorre mais rápido do que os núcleos podem responder. Quando o núcleo se realinha com a nova configuração eletrônica, a teoria afirma que ele deve passar por uma vibração.
Se a gente imagem vertical transição da terra para o estado eletrônico excitado como ocorrendo a partir de uma função de onda vibracional que dá uma distribuição de probabilidade de encontrar os núcleos em uma região do espaço, podemos determinar a probabilidade de um determinado nível vibracional da sobreposição integral \(S_{v’,v}\), o que dá a sobreposição da função de onda vibracional no chão e estado excitado. Os números quânticos \(v’\) referem-se ao estado do solo e os números quânticos \(v\) referem-se ao estado excitado. A probabilidade de transição pode ser separada em partes eletrônicas e nucleares usando a aproximação do condão.
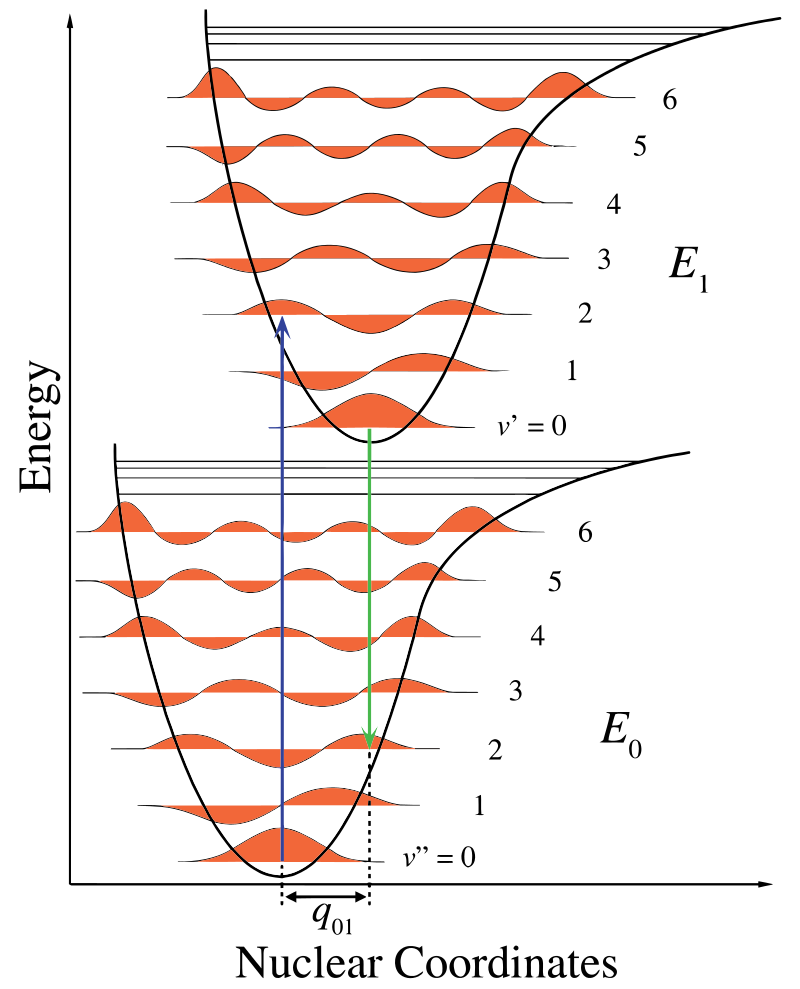
Na Figura \(\PageIndex{1}\), o eixo nuclear mostra uma consequência da separação internuclear e o vibronic transição é indicado pelo azul e verde setas verticais. Este número demonstra três coisas::uma absorção leva a um estado de energia mais elevado, a fluorescência conduz a um estado de energia mais baixo e o deslocamento das coordenadas nucleares entre o solo e o estado excitado é indicativo de uma nova posição de equilíbrio para o potencial de interacção nuclear. O fato de que a seta de fluorescência é mais curta do que a absorção indica que ela tem menos energia, ou que seu comprimento de onda é maior. a aproximação clássica do condão
aproximação do condão é a suposição de que a transição eletrônica ocorre em uma escala de tempo curta em comparação com o movimento nuclear de modo que a probabilidade de transição pode ser calculada em uma posição Nuclear fixa.esta mudança na vibração é mantida durante um estado denominado a excitação electrónica rápida. As forças Coulombianas resultantes produzem um equilíbrio como mostrado na figura para os núcleos denominados um ponto de viragem. O ponto de viragem pode ser mapeado desenhando uma linha vertical desde o mínimo da curva inferior até à intersecção do estado electrónico superior. Este procedimento é chamado de transição vertical e foi discutido antes no contexto da espectroscopia fotoeletrônica (outra espectroscopia eletrônica)..o princípio Franck-Condon explica as intensidades relativas das transições vibracionais relacionando a probabilidade de uma transição vibracional à sobreposição das funções das ondas vibracionais. Ele afirma que a probabilidade de uma transição vibracional ocorrendo é ponderada pelo Franck-Condon sobreposição integral:
\
Dentro de Franck-Condon aproximação, os núcleos são considerados “fixos” durante transições eletrônicas. Assim, transições eletrônicas podem ser consideradas transições verticais em curvas de energia potencial eletrônica (transições viéricas na figura \(\PageIndex{1}\)).
O princípio quântico Franck-Condon
O princípio Franck-Condon tem uma aplicação clássica e quântica. Classicamente, o princípio Franck–Condon é a aproximação de que uma transição eletrônica é mais provável de ocorrer sem alterações nas posições dos núcleos na entidade molecular e seu ambiente. O estado resultante é chamado de Estado Franck-Condon, e a transição envolvida, uma transição vertical. A formulação mecânica quântica deste princípio é que a intensidade de uma transição vibrônica é proporcional ao quadrado da integral sobreposta entre as ondulações vibracionais dos dois estados envolvidos na transição.
O princípio Franck-Condon é baseado na aproximação Born-Oppenheimer, que permite a separação das funções de onda eletrônica \(q\) e nuclear \(Q\) dada a função de onda total.
\
desde que o operador de transição, \(\hat {\mu} (q)\), depende apenas do componente electrónico, os componentes nucleares podem ser separados da integral do momento de transição que dita a probabilidade da transição ocorrer:
&= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{nuclear sobreposição}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle \end{align}\]
Se o nuclear sobreposição integral é zero para essa transição e, em seguida, a transição não será observado, independentemente da magnitude da electronic fator.
\(S_{00}\) transição avaliada dentro do modelo de oscilador harmônico
a sobreposição nuclear para a transição zero-zero \(S_{00}\) pode ser calculada simplesmente usando a definição da forma Gaussiana das ondulações harmônicas.
O ponto zero wavefunction no chão de estado eletrônico é
\
O ponto zero wavefunction no estado eletrônico excitado é
\
onde
- \(\alpha = \dfrac{\sqrt{mk}}{\hbar}\)
- \(R_e\) é o equilíbrio comprimento de ligação no chão electrónica do estado
- \(Q_e\) é o equilíbrio comprimento de ligação no estado eletrônico excitado
O nuclear sobreposição integral é
\
O expoente na Equação \(\ref{FC1}\) pode ser expandida como
\
e nós usamos
\
e
\
para substituir e completar o quadrado dentro da integral. Podemos expressar
\.\]
assim, o integral na equação \(\ref{FC2}\) é
\
o integral é um integral Gaussiano. Você pode mostrar que, se deixarmos \(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\), então \(dz = \sqrt{\alpha} dR\) e a integral torna-se
\
esta integral foi resolvido já, a partir de uma tabela de integrais, a Equação \(\ref{FC3}\) torna-se
\
Nós, siga o mesmo procedimento para calcular a sobreposição do zeroth nível de vibração no solo para o primeiro animado nível vibracional do estado excitado: \(S_{01}\).
\(S_{01}\) de Transição Avaliados dentro de Oscilador Harmônico Modelo
Para calcular a sobreposição de zeroth solo em nível de estado (\(v=0\)) com o primeiro estado excitado (nível de\(v’=1\)) usamos o polinˆ omio de Hermite \(H_1(x) =2x\) para descrever o estado excitado wavefunction (veja aqui uma análise sobre o oscilador harmônico wavefunctions). Aqui \(x = \sqrt {\alpha} (R – Q_e)\).
\
com o ponto zero wavefunction no chão de estado eletrônico é
\
O primeiro animado-estado wavefunction no estado eletrônico excitado é
\
A sobreposição de zeroth solo em nível de estado, com o primeiro estado excitado (nível de Equação \(\ref{FC01}\)) é, em seguida,
\
e
\
O mesmo substituições podem ser feitas como acima, de modo que a integral pode ser escrita como (não mostrado e demonstrado em uma lição de exercícios) e o resultado final é
\
Podemos Continuar e calcular a sobreposição do nível zeroth no estado do solo com todos os níveis vibracionais de luz mais elevados: \(S_{02}\), \(s_{03}\), etc. Cada termo corresponde a uma transição com uma energia diferente, uma vez que os níveis vibracionais têm energias diferentes. A banda de absorção então tem o aparecimento de uma progressão (uma progressão Franck-Condon) de transições entre diferentes níveis cada um com sua própria probabilidade.
progressões de condão Franck
para compreender o significado da fórmula acima para o factor FC, vamos examinar uma superfície de energia potencial de estado excitado em \(T = 0\) Kelvin. Mostrados abaixo estão dois estados separados por 8.000 cm – 1 em energia. Esta é a separação de energia entre os fundos de seus potenciais poços, mas também entre os respectivos níveis de energia de ponto zero. Vamos supor que o número de onda do modo vibracional é de 1.000 cm-1 e que o comprimento da ligação é aumentado devido ao fato de que um elétron é removido de um orbital de ligação e colocado em um orbital anti-ligação sobre excitação eletrônica.
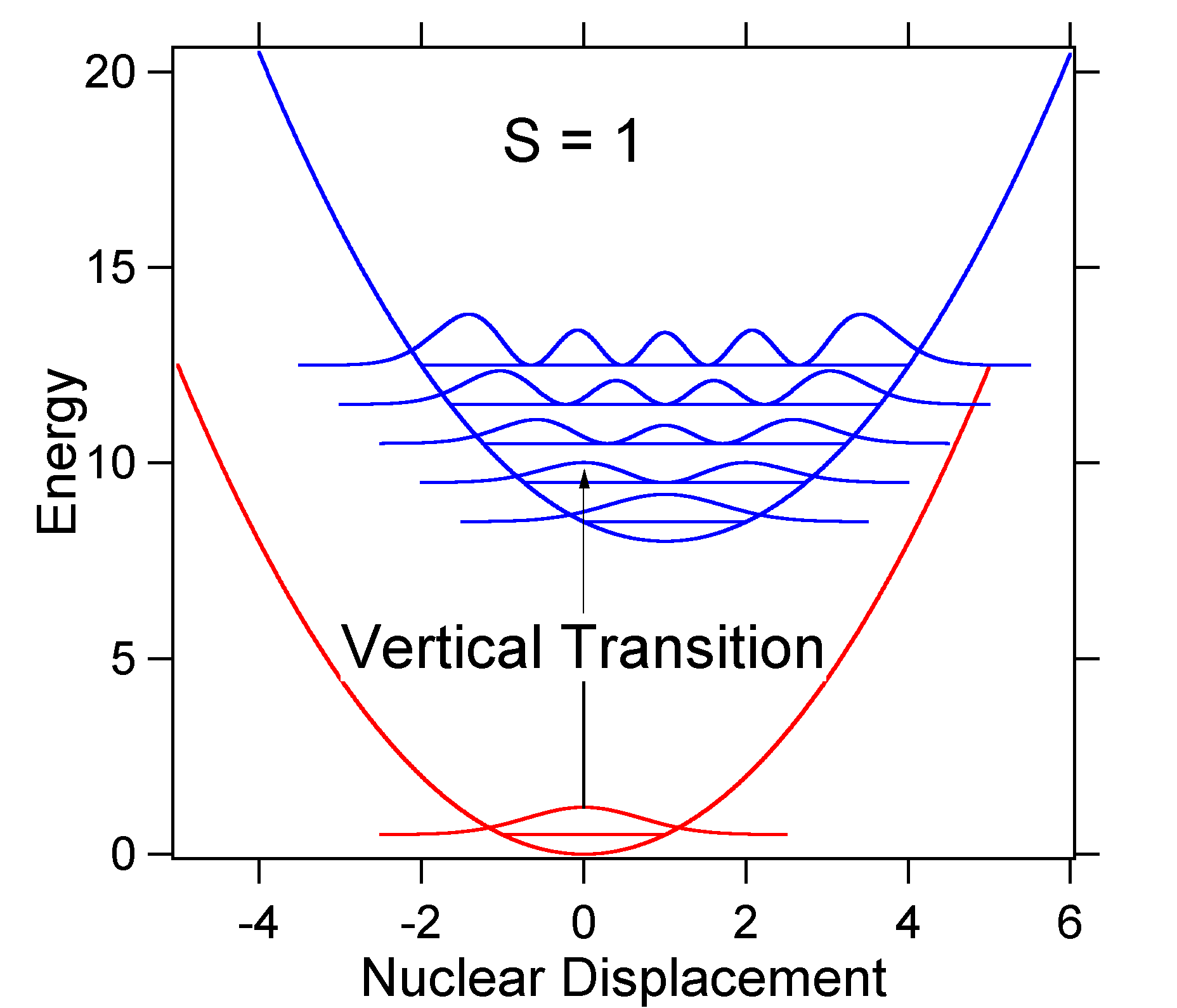
de Acordo com o modelo acima para o Franck-Condon fator que poderia gerar um “stick” de espectro (Figura \(\PageIndex{3}\)), onde cada transição vibracional é infinitamente estreita e de transição só pode ocorrer quando \(E = h\nu\) exatamente. Por exemplo, as superfícies de energia potencial foram dadas para S = 1 e a probabilidade de transição em cada nível é dada pelas varas (preto) na figura abaixo.
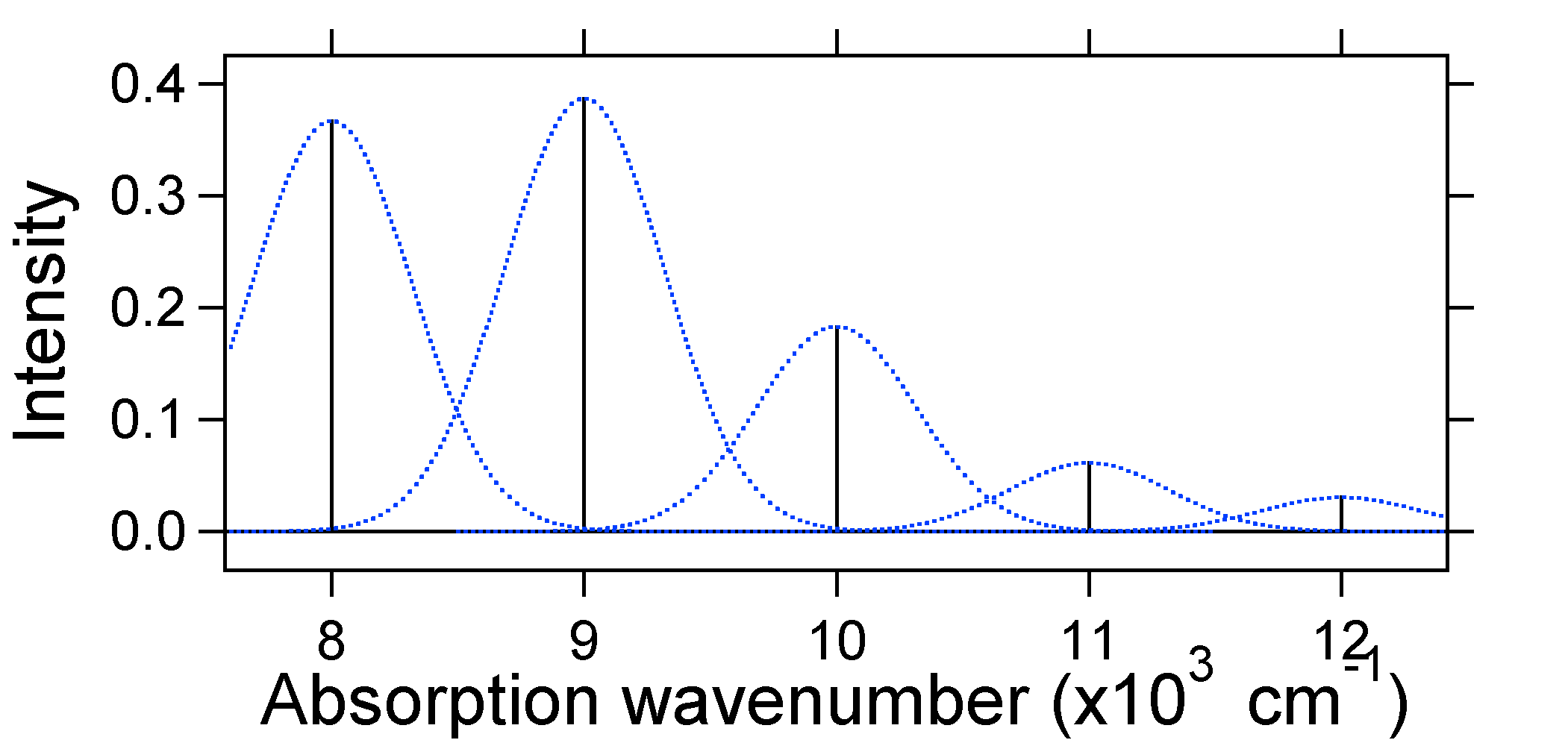
os Gaussianos pontilhados que rodeiam cada pau dão uma imagem mais realista do que o espectro de absorção deve parecer. Neste primeiro lugar, cada nível de energia (Pau) será dada alguma largura pelo fato de que o estado tem uma vida útil finita. Tal ampliação é chamada de ampliação homogênea uma vez que afeta todas as moléculas no conjunto de uma forma similar. Há também um alargamento devido a pequenas diferenças no ambiente de cada molécula. Este tipo de ampliação é chamado de ampliação não homogênea. Independentemente da origem, o modelo acima foi criado usando um alargamento Gaussiano
O deslocamento nuclear entre o solo e o estado excitado determina a forma do espectro de absorção. Examinemos tanto um deslocamento de Estado menor quanto um grande deslocamento de estado excitado. Se \(S = ½\) e a energia potencial superfícies, neste caso, são:
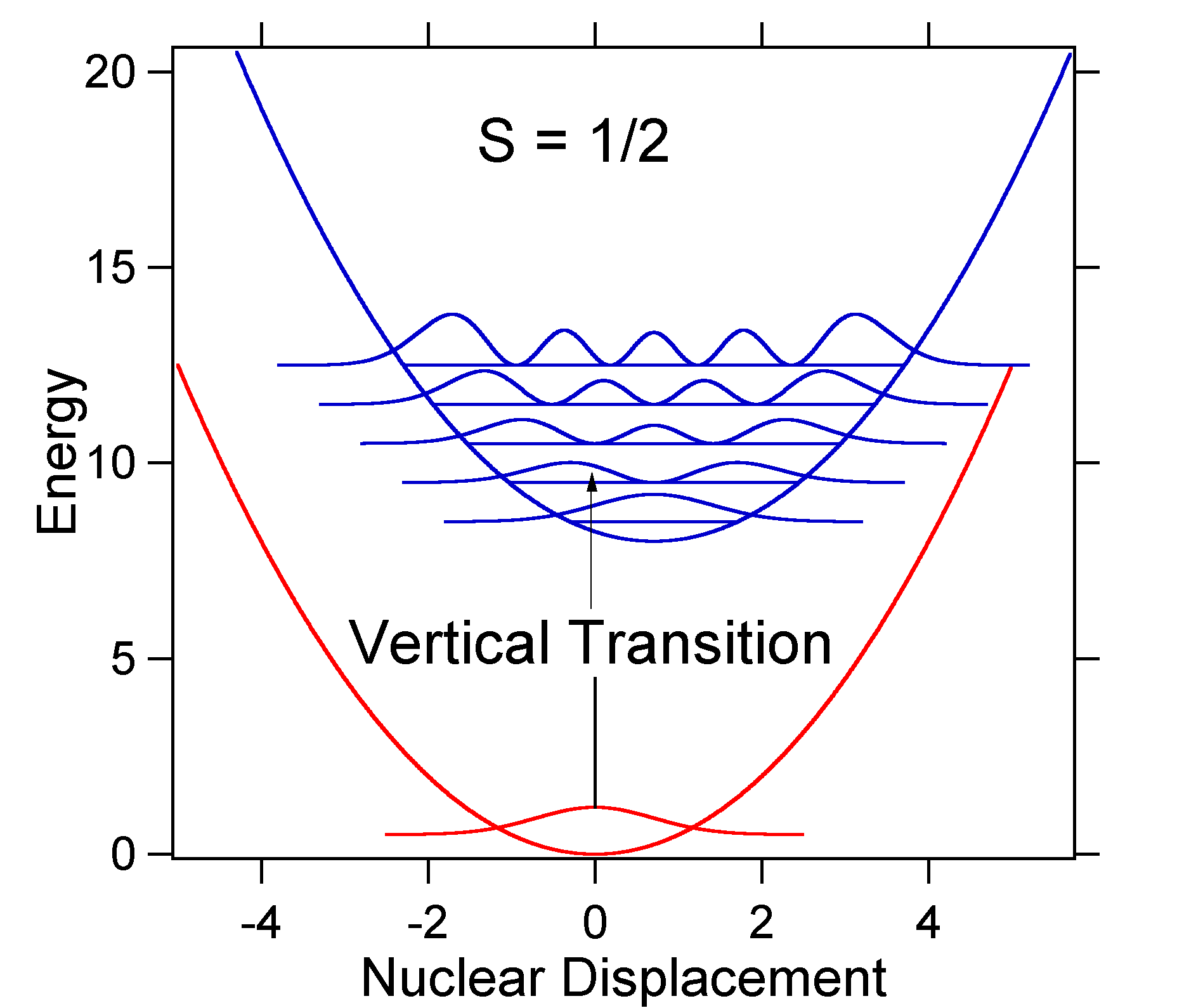
For this case the “stick” spectrum has the appearance in Figure \(\PageIndex{5}\)
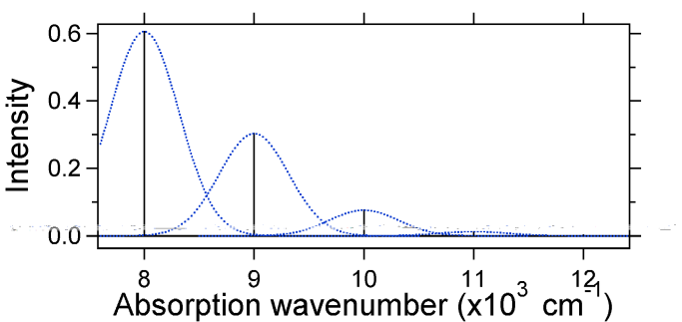
Note que a transição vibracional zero-zero ou \(S_{0,0}\) é muito grande no caso em que o deslocamento é pequeno.
como regra geral, a constante \(s\) dá a razão da intensidade da transição \(v = 2\) para a transição \(v = 1\). Neste caso, desde \(S = 0.5\), a transição \(v=2\) é 0.5 A intensidade da transição \(v=1\).
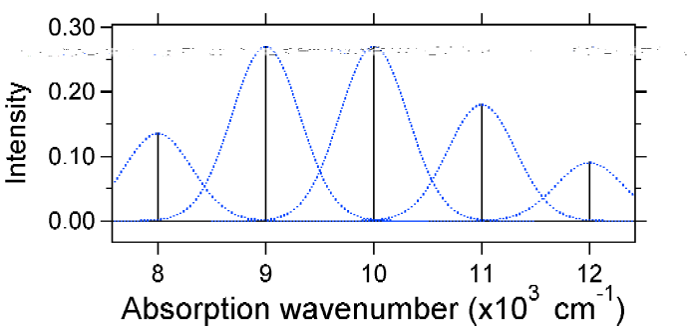
como exemplo de um deslocamento maior, a disposição das superfícies de energia potencial para S = 2 é mostrada abaixo.
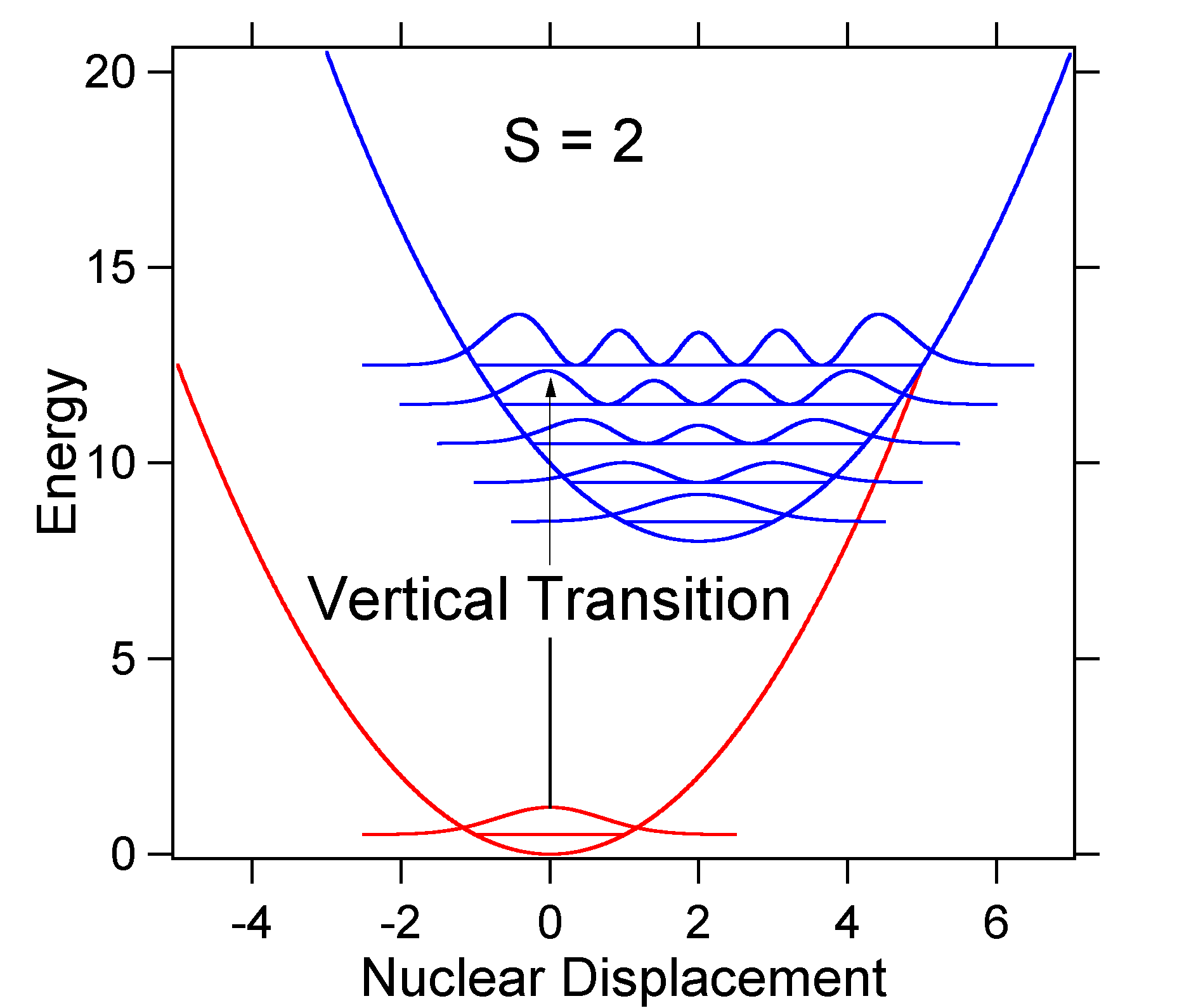
o deslocamento maior resulta em diminuição da sobreposição do nível do Estado do solo com o Nível v = 0 do estado excitado. A intensidade máxima será alcançada em níveis vibracionais mais elevados, como mostrado no espectro de vara.
os espectros de absorção plotados abaixo têm a mesma intensidade integrada, no entanto suas formas são alteradas devido à diferente extensão do deslocamento da superfície de energia potencial do estado excitado.
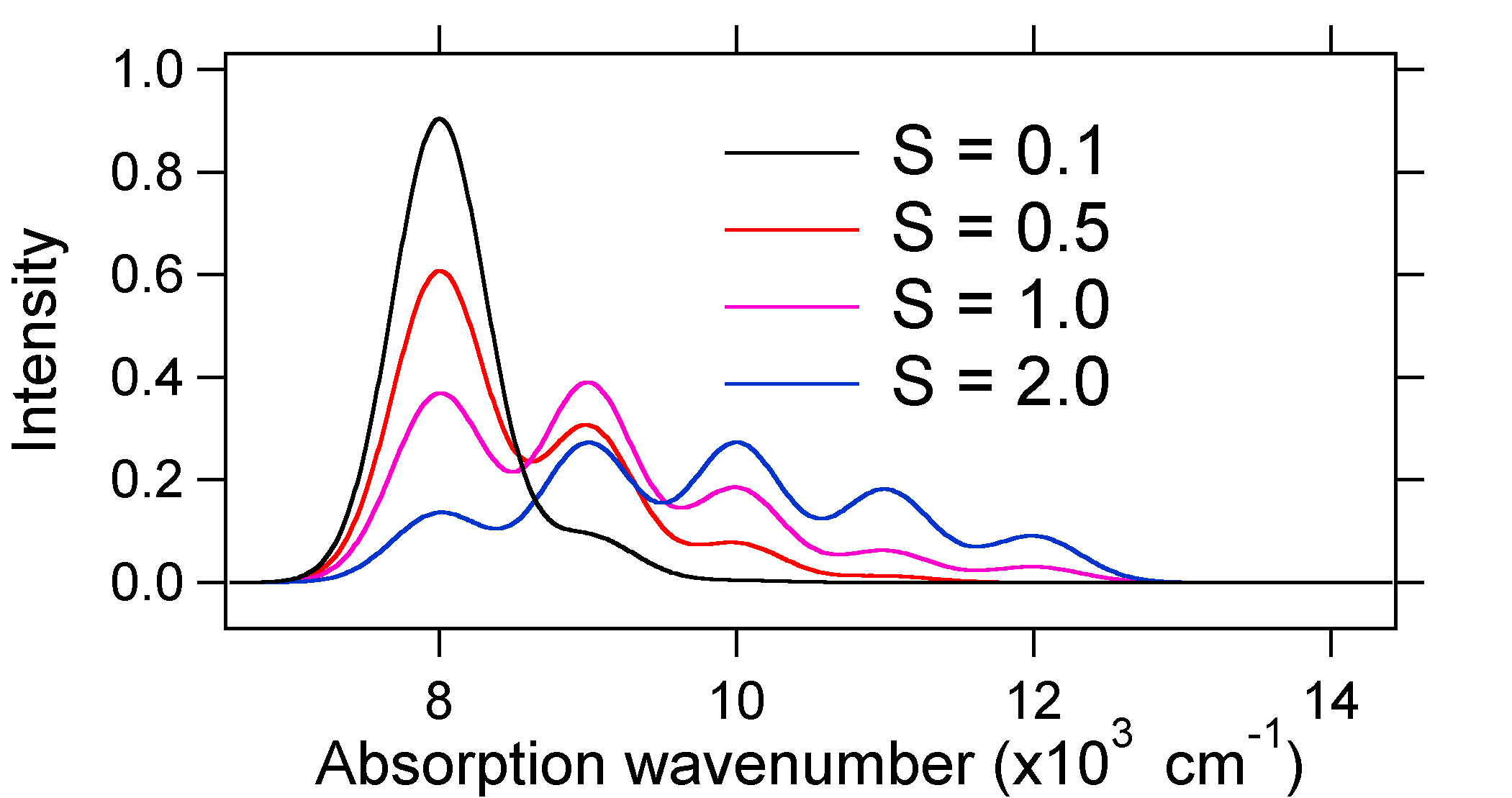
de modo que a natureza das intensidades de banda vibrônica relativa pode nos dizer se existe um deslocamento da coordenada nuclear de equilíbrio que acompanhou uma transição. Quando haverá um aumento no comprimento das obrigações (isto é, \(Q_e > R_e\)? Isto ocorre quando um elétron é promovido de um orbital molecular de ligação a um orbital molecular Não-ligação ou anti-ligação (isto é, quando a ordem de ligação é menos no estado excitado do que o estado do solo).
- Não-ligação orbital molecular \(\rightarrow\) fixação de orbitais moleculares
- Anti-ligação orbital molecular \(\rightarrow\) fixação de orbitais moleculares
- Anti-ligação orbital molecular \(\rightarrow\) não-ligação orbital molecular
Em suma, quando a ordem de ligação é menor no estado excitado do que no estado fundamental, então \(Q_e > R_e\); um aumento na bondlength irá ocorrer quando isso acontece.
- J. M. Luis, D. M. Bishop, B. Kirtman. A different approach for calculating Franck-Condon factors including anharmonicity. J. Chem. Phys., 120 (2004), pp. 813-822.Atkins, Peter e Julio De Paula. Física Química para as ciências da vida. 2006. New York, NY: W. H. Freeman and Company. P. 563-564
- Franck-Condon Principle. 1996, 68, 2243. IUPAC Compendium of Chemical Terminology 2nd Edition (1997). www.iupac.org/goldbook/F02510.pdf E. Rabinowitch e Govindjee. Absorção de luz e destino da excitação da energia. 1969. Princípio Franck-Condon. http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
Contribuintes
- Matthe Zi Ziering
-
Stefan Franzen (North Carolina State University)