Supervisionada Inferência Bayesiana (redução de dimensões e de liberação de recursos)
Baixo nível de funcionalidade de detecção de bordas

Finalmente, o momento que você tem todos estavam esperando, o próximo na nossa supervisionada inferência Bayesiana série: Nossa (não tão) aprofundar o Operador de Sobel.
um algoritmo de detecção de borda verdadeiramente mágico, que permite a extração de recursos de baixo nível e redução de dimensionalidade, essencialmente reduzindo o ruído na imagem. Tem sido particularmente útil em aplicações de reconhecimento facial.
the 1968 love child of Irwin Sobel and Gary Feldman( Stanford Artificial Intelligence Laboratory), this algorithm was the inspiration of many modern edge detection techniques. Convulsionando dois núcleos opostos ou máscaras sobre uma determinada imagem (e.g. veja abaixo-esquerda) (cada um capaz de detectar as arestas horizontais ou verticais), podemos criar uma representação menos barulhenta e suavizada (ver abaixo-direita).
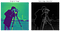
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel valores (normalmente luminância) diferenciando a diferença entre cada pixel (o pixel âncora) e os seus pixels circundantes (essencialmente aproximando a derivada de uma imagem).
isto resulta em suavizar a imagem original e produzir uma saída menor dimensão, onde as características geométricas de baixo nível podem ser vistas mais claramente. Estas saídas podem então ser usadas como entradas em algoritmos de classificação mais complexos, ou como exemplos usados para clustering probabilístico não supervisionado via Kullback-Leibler Divergence (KLD) (como visto no meu blog recente no LBP).a geração da nossa saída de menor dimensão requer que tomemos a derivada da imagem. Primeiro, calculamos a derivação nas direções x e Y. Nós criamos dois núcleos 3×3( veja matrizes), com zeros ao longo do centro do eixo correspondente, dois nos quadrados centrais perpendiculares ao zero central e uns em cada um dos cantos. Cada um dos valores não-zero deve ser positivo no topo/à direita dos zeros (dependentes do eixo) e negativo no lado correspondente. Estes núcleos são chamados Gx e Gy.
estes aparecem no formato:
Estes núcleos serão, em seguida, convolve sobre nossa imagem, colocando o pixel central de cada kernel sobre cada pixel da imagem. Nós usamos a multiplicação de matriz para calcular o valor de intensidade de um novo pixel correspondente em uma imagem de saída, para cada kernel. Portanto, acabamos com duas imagens de saída (uma para cada direção cartesiana).
O objectivo é encontrar a diferença / alteração entre o pixel na imagem e todos os pixels na matriz do gradiente (kernel) (Gx e Gy). Mais matematicamente, isto pode ser expresso como.nota lateral: não estamos, tecnicamente, a conviver com nada. Embora gostemos de nos referir a ‘convoluções’ em círculos de aprendizagem de IA e máquina, uma convolução envolveria virar a imagem original. Matematicamente falando, quando nos referimos a convoluções, estamos realmente calculando a correlação cruzada entre cada área 3×3 da entrada e a máscara para cada pixel. A imagem de saída é a covariância global entre a máscara e a entrada. É assim que as bordas são detectadas.
de volta à nossa explicação Sobel …
os valores calculados para cada multiplicação de matriz entre a máscara e a secção 3×3 da entrada são somados para produzir o valor final para o pixel na imagem de saída. Isto gera uma nova imagem que contém informações sobre a presença de arestas verticais e horizontais presentes na imagem original. Esta é uma representação geométrica da imagem original. Além disso, como este operador é garantido para produzir a mesma saída cada vez, esta técnica permite a detecção de borda estável para tarefas de segmentação de imagem.
a Partir desses resultados, podemos calcular o gradiente magnitude e a direção de inclinação (usando o arco tangente do operador) em qualquer pixel (x,y):
a Partir desta podemos verificar que os pixels com grande magnitude são mais propensos a ser uma borda na imagem, enquanto a direção informa-nos sobre a orientação de borda (embora a direção não é necessária para gerar a nossa saída).uma implementação simples:
Aqui está uma implementação simples do operador Sobel em python (usando o NumPy) para lhe dar uma ideia do processo (para todos os programadores que estão em formação).
Esta implementação é um python variante da Wikipédia exemplo de pseudocódigo, com o objetivo de mostrar como você pode implementar esse algoritmo, ao mesmo tempo, demonstrando as várias etapas do processo.por que nos importamos?
embora a aproximação gradiente produzida por este operador seja relativamente crua, ele fornece um método extremamente eficiente de computação de arestas, cantos e outras características geométricas de imagens. Por sua vez, abriu o caminho para uma série de redução de dimensionalidade e técnicas de extração de recursos, tais como padrões binários locais (Veja meu outro blog para mais detalhes sobre esta técnica).
Depender exclusivamente características geométricas não o risco de perder informações importantes durante a codificação de nossos dados, no entanto, o trade-off é o que permite a rápida pré-processamento dos dados e, por sua vez, treinamento rápido. Portanto, esta técnica é especialmente útil em cenários onde a textura e as características geométricas podem ser consideradas altamente importantes na definição da entrada. É por isso que o reconhecimento facial pode ser completado com um grau relativamente elevado de precisão usando o operador Sobel. No entanto, esta técnica pode não ser a melhor escolha se se tentar classificar ou agrupar entradas que utilizam a cor como seu principal fator de diferenciação.
este método ainda é extremamente eficaz para ganhar uma representação de baixa dimensão de características geométricas e um excelente ponto de partida para dimensionalidade e redução de ruído, antes de usar outros classificadores ou para uso em metodologias de Inferência Bayesiana.