Compreensing Deep Residual Networks

Deep residual networks (ResNet) took the deep learning world by storm when Microsoft Research released Deep Residual Learning for Image Recognition. Estas redes levaram a entradas em primeiro lugar nas cinco principais faixas das competições ImageNet e COCO 2015, que cobriram a classificação de imagens, detecção de objetos e segmentação semântica. A robustez dos ResNets tem sido provada desde então por várias tarefas de reconhecimento visual e por tarefas não-visuais envolvendo fala e linguagem. Eu também usei a ResNet, além de outros modelos de aprendizagem profunda na minha pesquisa de dissertação de Phd.

Este post vai resumir os três trabalhos abaixo, que são todos escritos ou co-escritos pelo inventor de ResNet Kaiming He, porque eu acredito que os trabalhos originais dar a explicação mais intuitiva e detalhada do modelo/redes. Esperançosamente, este post poderia ajudá-lo a obter uma melhor compreensão do gist das redes residuais.

• Profundo Residual de Aprendizagem para Reconhecimento de Imagem
• Identidade mapeamentos em Profunda Residual Redes
• Agregado Residual Transformação Profunda Redes Neurais

Intuição Profunda Residual de Rede (stackoverflow ref)

Um residual de bloqueio é exibida como a seguir:

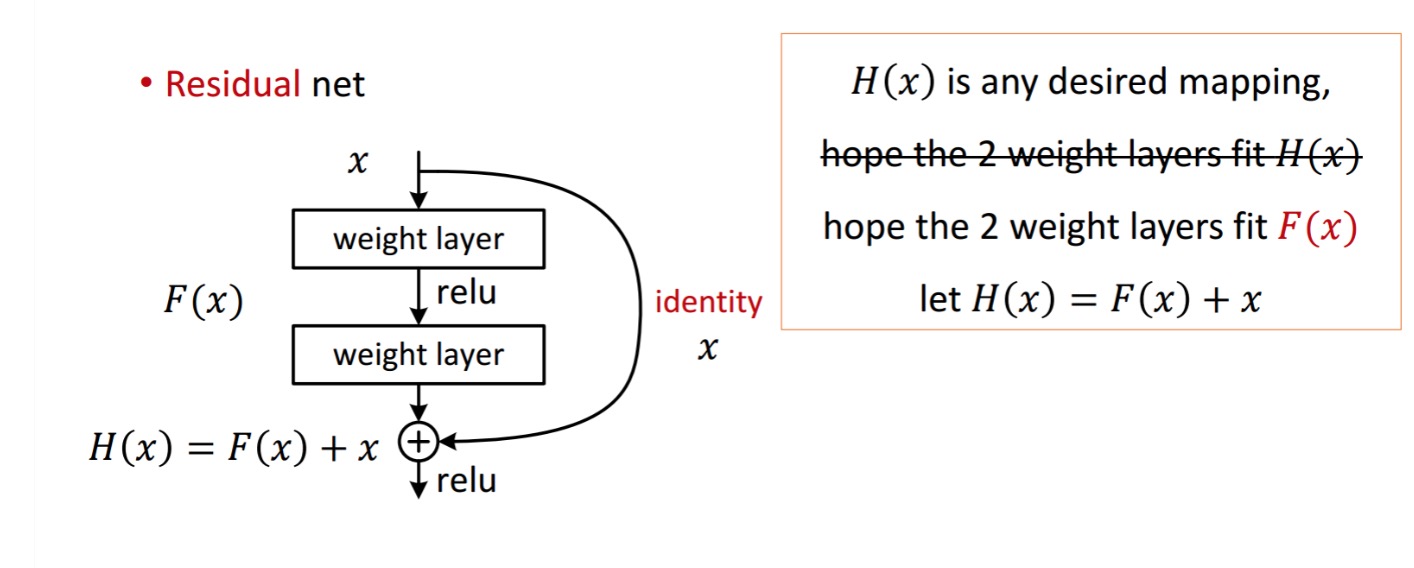
Então, o residual unidade mostrada obtém por tratamento com dois peso camadas. Em seguida, acrescenta-se a obter . Agora, assume que essa é a tua saída prevista ideal que corresponde à tua verdade. Desde, obter o desejado depende de obter o perfeito . Isso significa que as duas camadas de peso na unidade residual deve realmente ser capaz de produzir o desejado , em seguida, obter o ideal é garantido.

é obtido do seguinte modo:

é obtido do seguinte modo:

os autores sugerem que o mapeamento residual (i.e. ) pode ser mais fácil de otimizar do que . Para ilustrar com um exemplo simples, assumir que o ideal . Então, para um mapeamento direto seria difícil aprender um mapeamento de identidade como há uma pilha de camadas não-lineares como se segue.assim, aproximar o mapeamento de identidade com todos estes pesos e ReLUs no meio seria difícil.

Agora, se definirmos o mapeamento desejado, então só precisamos de obter o seguinte.alcançar o acima é fácil. Basta definir qualquer peso para zero e você terá uma saída zero. Adicionar de volta e você obter o seu mapeamento desejado.

aprendizagem Residual profunda para o reconhecimento de imagens

problema

quando redes mais profundas começam a convergir, um problema de degradação foi exposto: com o aumento da profundidade da rede, a precisão fica saturada e então degrada-se rapidamente.

ver degradando-se em ação:

tomemos uma rede rasa e a sua contrapartida mais profunda, adicionando-lhe mais camadas.

pior cenário: as camadas iniciais do modelo mais profundo podem ser substituídas por uma rede rasa e as camadas restantes podem apenas agir como uma função de identidade (entrada igual à saída).

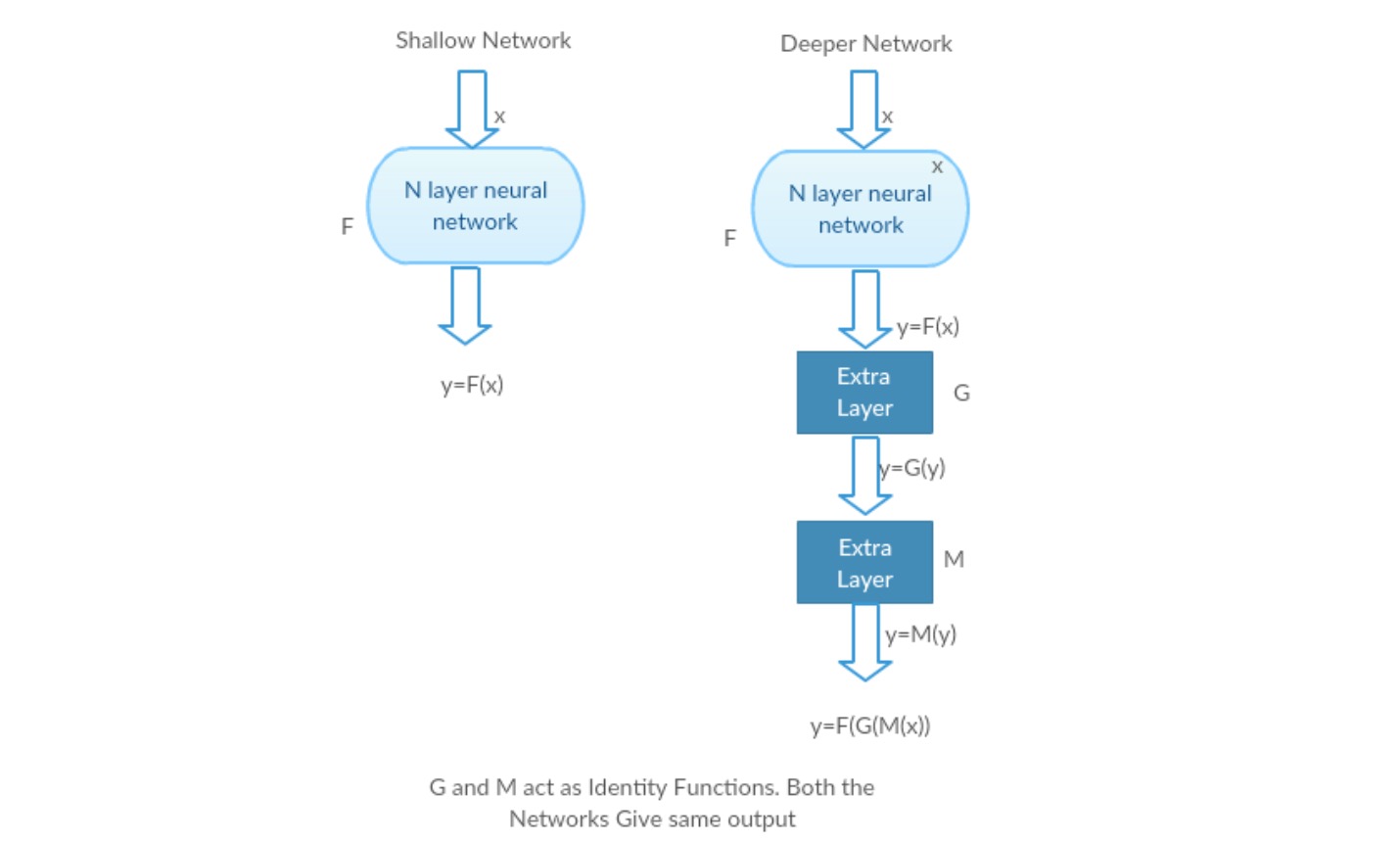
cenário gratificante: na rede mais profunda, as camadas adicionais aproximam melhor o mapeamento do que a parte do contador mais raso e reduz o erro por uma margem significativa.experiência: Na pior das hipóteses, tanto a rede rasa como a variante mais profunda dela devem dar a mesma precisão. No cenário recompensador, o modelo mais profundo deve dar uma precisão melhor do que a parte do contador mais raso. Mas as experiências com os nossos actuais solucionadores revelam que modelos mais profundos não funcionam bem. Assim, o uso de redes mais profundas está degradando o desempenho do modelo. Estes trabalhos tentam resolver este problema usando uma estrutura de aprendizagem Residual profunda.como resolver?

em vez de aprender um mapeamento direto com uma função (algumas camadas não-lineares empilhadas). Vamos definir a função residual usando, que pode ser reformulada em, onde e representa as camadas não-lineares empilhadas e a função identidade(entrada=saída), respectivamente.

a hipótese do autor é que é fácil otimizar a função de mapeamento residual do que otimizar o mapeamento original, não referenciado .

intuição atrás de blocos residuais:

vamos tomar o mapeamento de identidade como um exemplo (por exemplo ). Se o mapeamento de identidade é ideal, podemos facilmente empurrar os resíduos para zero () do que para caber um mapeamento de identidade () por uma pilha de camadas não-lineares. Em linguagem simples, é muito fácil chegar a uma solução como, ao invés de usar pilha de camadas cnn não lineares como função (pense nisso). Então, esta função é o que os autores chamaram de função Residual.

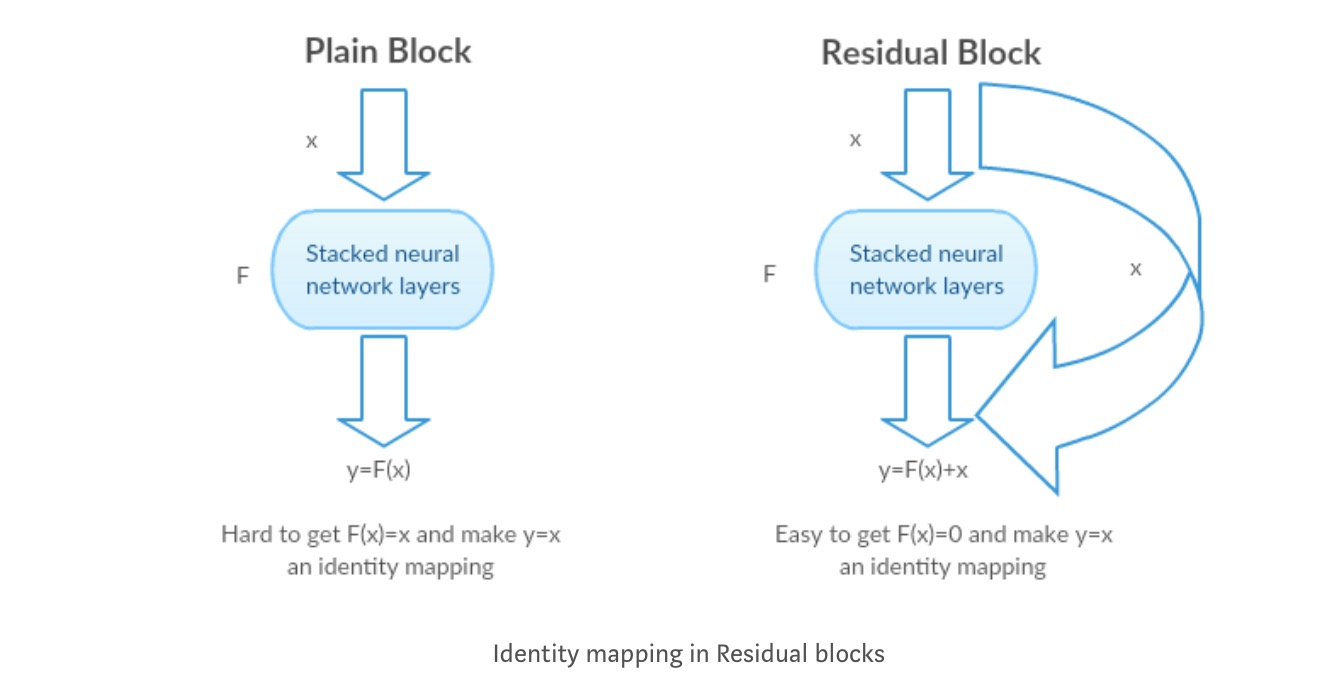
os autores fizeram vários testes para testar a sua hipótese. Vamos olhar para cada um deles agora.

casos de ensaio:

tomar uma rede simples (rede de camada VGG kind 18) (rede-1) e uma variante mais profunda dela (34-camada, rede-2) e adicionar camadas residuais à rede-2 (34 camada com conexões residuais, rede-3).

desenhando a rede:

1. utilize 3 * 3 filtros principalmente.amostragem com camadas CNN com stride 2.
2. camada global média de agrupamento e uma camada de 1000 vias totalmente conectada com Softmax no final.

Existem dois tipos de ligações residuais:

I. os atalhos de identidade () podem ser directamente utilizados quando a entrada () e a saída () têm as mesmas dimensões.

II. quando as dimensões mudam, A) o atalho ainda executa mapeamento de identidade, com entradas extra-zero acolchoadas com a dimensão aumentada. B) o atalho de projeção é usado para corresponder à dimensão (feito por 1*1 conv) usando a seguinte fórmula

resultados

mesmo que a rede de 18 camadas seja apenas o subespaço na rede de 34 camadas, ele ainda funciona melhor. ResNet supera por uma margem significativa no caso, a rede é mais profundo

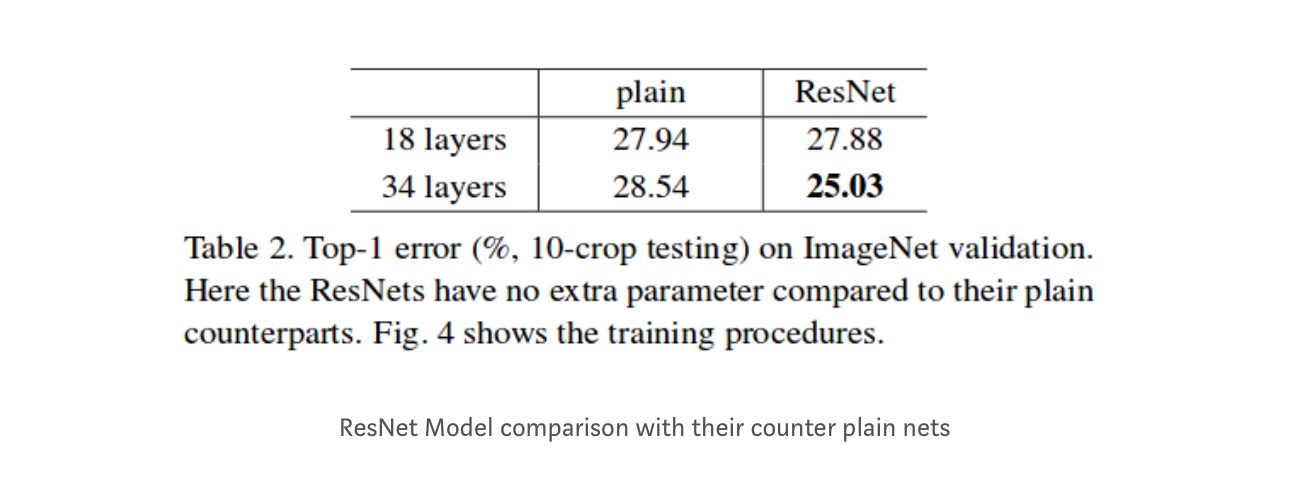
estudos mais aprofundados

Além disso, mais redes são estudados:

Cada ResNet bloco é de 2 camadas profundas (Usado em pequenas redes como o ResNet 18, 34) ou 3 camadas profundas( ResNet 50, 101, 152).

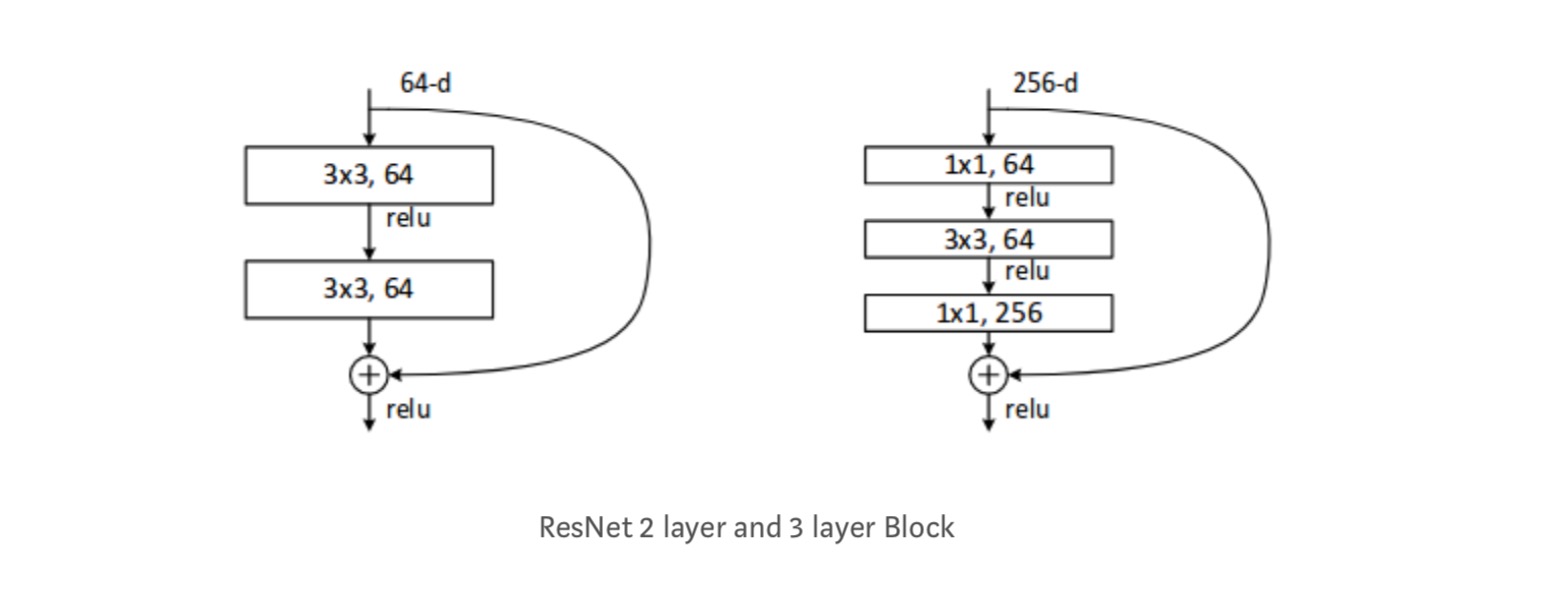
observações

1. rede ResNet Converge mais rapidamente em comparação com a parte do contador simples.identidade vs projeção shorcuts. Ganhos incrementais muito pequenos usando atalhos de projeção (equação-2) em todas as camadas. Assim, todos os blocos de ResNet usam apenas atalhos de identidade com atalhos de projeção usados apenas quando as dimensões mudam.ResNet-34 obteve um erro de validação top-5 de 5,71% melhor que BN-inception e VGG. A ResNet-152 atinge um erro de validação top-5 de 4,49%. Um conjunto de 6 modelos com diferentes profundidades atinge um erro de validação top-5 de 3,57%. Ganhar o 1º lugar em ILSVRC-2015

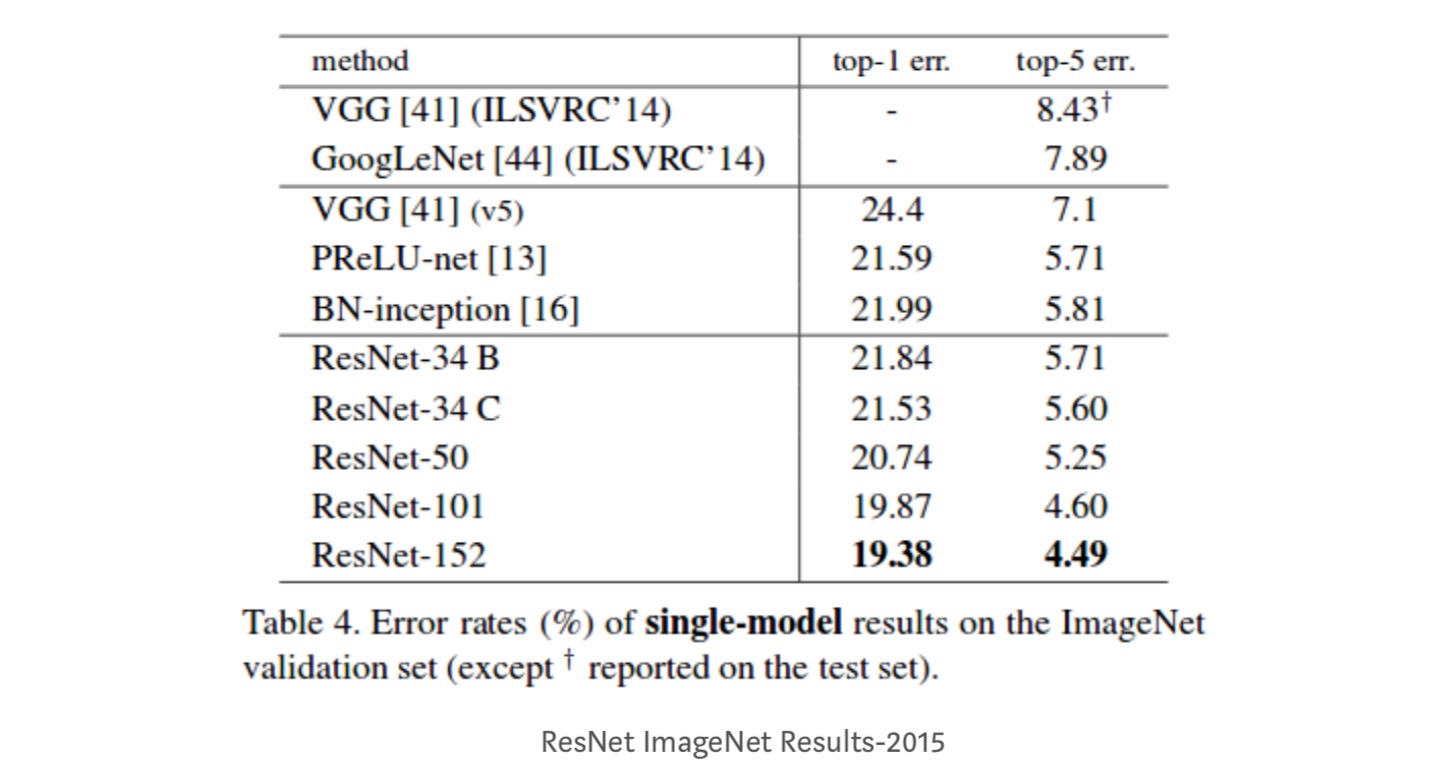
Identidade mapeamentos em Profunda Residual Redes

Este documento dá a compreensão teórica do porquê de fuga gradiente problema não está presente na Residuais redes e o papel de ignorar ligações (ignorar ligações significar a entrada ou ) substituindo o mapeamento de Identidade (x) com diferentes funções.

introdução

redes residuais profundas consistem em muitas “unidades residuais”empilhadas. Cada unidade pode ser expressa em uma forma geral:

Onde e são entrada e saída da unidade, e é uma função residual. No último artigo, é um mapeamento de identidade e é uma função ReLU.

A ideia central das redes é aprender a função residual aditivo em relação a , com uma escolha chave de usar um mapeamento de identidade . Isto é realizado anexando uma conexão de salto de identidade (“atalho”).

neste artigo, analisamos redes residuais profundas, concentrando-nos na criação de um caminho” direto ” para a propagação da informação — não só dentro de uma unidade residual, mas através de toda a rede. Nossas derivações revelam que se ambos e são mapeamentos de identidade, o sinal poderia ser propagado diretamente de uma unidade para qualquer outra unidade, em ambos os passos para a frente e para trás. Nossas experiências empiricamente mostram que o treinamento em geral se torna mais fácil quando a arquitetura está mais próxima das duas condições acima.

para compreender o papel das conexões de salto, analisamos e comparamos vários tipos de . Descobrimos que o mapeamento de identidade escolhido no último artigo atinge a redução mais rápida de erros e a menor perda de treinamento entre todas as variantes investigadas, enquanto as conexões de salto em escala, Gate e convoluções de 1×1 levam a maior perda de treinamento e erro. Estes experimentos sugerem que manter um caminho de informação “limpo” é útil para facilitar a otimização.

para construir um mapeamento de identidade, nós vemos as funções de ativação (ReLU E BN) como “pré-ativação” das camadas de peso, em contraste com a sabedoria convencional de “pós-ativação”. Este ponto de vista leva a uma nova concepção de unidade residual, mostrada na figura seguinte. Com base nesta unidade, apresentamos resultados competitivos em CIFAR-10/100 com uma ResNet de 1001 camadas, que é muito mais fácil de treinar e generaliza melhor do que a ResNet original. Nós também relatamos melhores resultados no ImageNet usando uma ResNet de 200 camadas, para a qual a contraparte do último artigo começa a exagerar. Estes resultados sugerem que há muito espaço para explorar a dimensão da profundidade da rede, uma chave para o sucesso da aprendizagem profunda moderna.

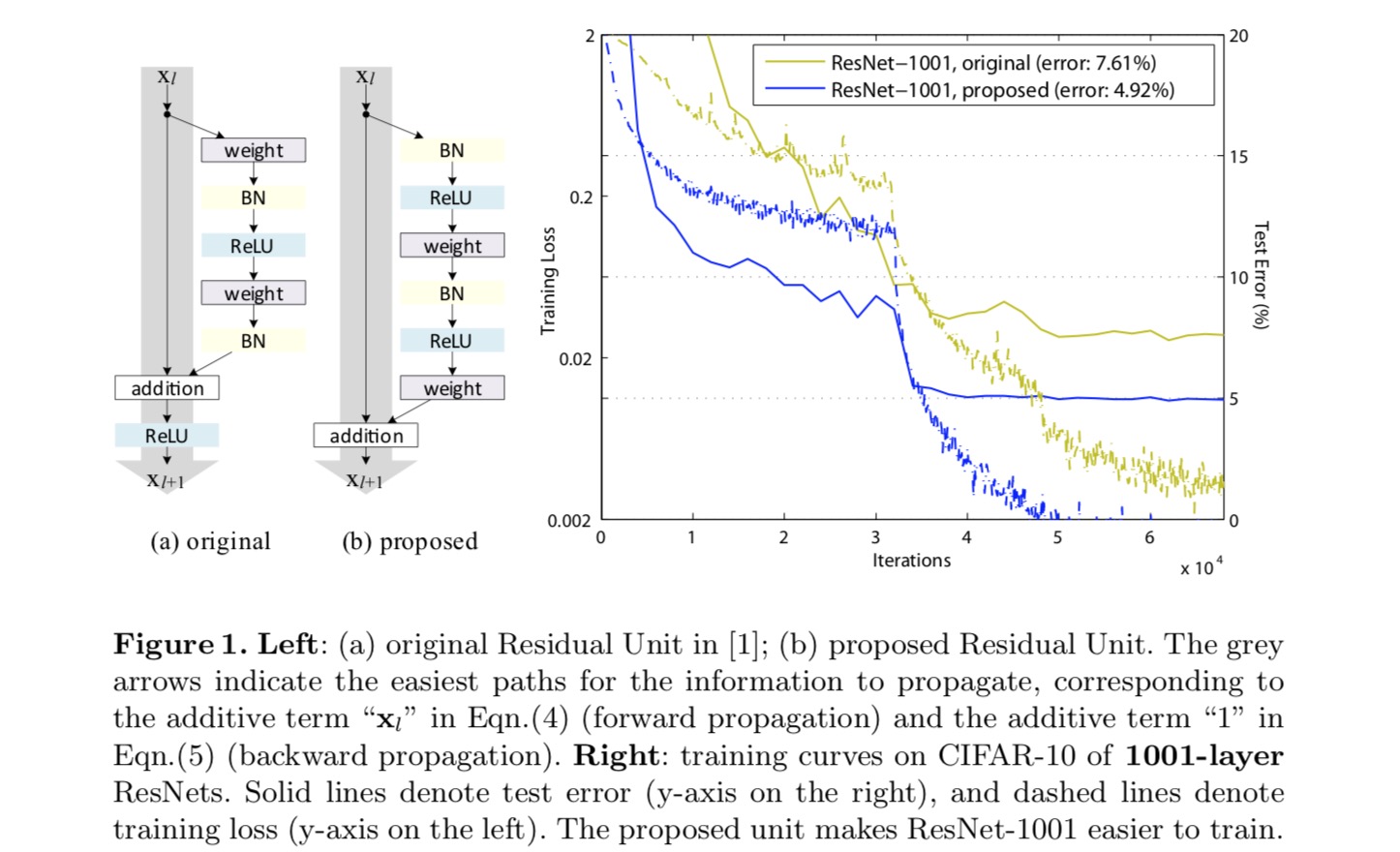
Análise de redes residuais profundas

As redes desenvolvidas no último papel são arquitecturas modularizadas que empilham blocos de construção da mesma forma de ligação. Neste artigo chamamos a estes blocos “unidades residuais”. A unidade Residual original no último artigo executa o seguinte cálculo:

Aqui está a funcionalidade de entrada para a-ésima unidade Residual. é um conjunto de pesos (e vieses) associados com a-ésima unidade Residual, e é o número de camadas em uma unidade Residual ( é 2 ou 3 no último papel). indica a função residual, E.G., uma pilha de duas camadas convolucionais de 3×3 no último papel. A função é a operação após adição elemento-sábio, e no último artigo é ReLU. A função é definida como um mapeamento de identidade: .

If is also an identity mapping: , we can obtain:

Recursively we will have:

for any deeper unit and any shallower unit . Esta equação exibe algumas nicepropertias. (1) A característica de qualquer unidade mais profunda pode ser representada como a característica de qualquer unidade menos rasa mais uma função residual em uma forma de , indicando que o modelo é de forma residual entre quaisquer unidades e . (2) a característica , de qualquer unidade profunda , é a soma das saídas de todas as funções residuais anteriores (mais). Isto é em contraste com uma” rede simples ” onde uma característica é uma série de produtos matriz-vetor, digamos, (ignorando BN e ReLU).

a equação acima também leva a boas propriedades de propagação para trás. Denotando a função de perda como, a partir da regra da cadeia de contrapropagação temos:

a equação acima indica que o gradiente pode ser decomposto em dois termos aditivos: um termo que propaga informação diretamente sem relação com qualquer camada de peso, e outro termo que se propaga através das camadas de peso. O aditivo de prazo do garante que a informação está diretamente propagada de volta para qualquer menor unidade l. A equação acima também sugere que é improvável que o gradiente para ser canceladas para um mini-lote, porque, em geral, o termo não pode ser sempre -1 para todas as amostras em um mini-lote. Isto implica que o gradiente de uma camada não desaparece mesmo quando os pesos são arbitrariamente pequenos.

As duas equações acima sugerem que o sinal pode ser propagado diretamente de qualquer unidade para outra, tanto para a frente como para trás. A fundação das duas primeiras equações acima são dois mapeamentos de identidade: (1) a conexão de skip identidade , e (2) a condição que é um mapeamento de identidade.

importância das ligações de salto de identidade

vamos considerar uma modificação simples, para quebrar o atalho de identidade:

Onde é um escalar modulador (para a simplicidade que ainda assumimos ser identidade). Aplicando recursivamente esta formulação obtemos uma equação semelhante à acima:onde a notação absorve os escalares nas funções residuais. Similarmente, temos a contrapropagação da seguinte forma:

Ao contrário da equação anterior, nesta equação o primeiro termo aditivo é modulado por um fator . Para uma rede extremamente profunda (é grande), se para todos , este fator pode ser exponencialmente grande; se para todos , este fator pode ser exponencialmente pequeno e desaparecer, o que bloqueia o sinal de backpropagated a partir do atalho e força-o a fluir através das camadas de peso. Isso resulta em dificuldades de otimização como mostramos por experimentos.

na análise acima, a ligação de salto de identidade original é substituída por uma escala simples . Se a conexão skip representa transformações mais complicadas (tais como convoluções de Gate e 1×1), na equação acima o primeiro termo torna-se onde é a derivada de . Este produto pode também impedir a propagação da informação e dificultar o processo de formação, tal como testemunhado nas experiências seguintes.experimentamos com a ResNet de 110 camadas em CIFAR-10. Esta ResNet-110 extremamente profunda tem 54 unidades residuais de duas camadas (consistindo de 3×3 camadas convolucionais) e é um desafio para a otimização. Vários tipos de conexões de salto são experimentados. Veja a figura a seguir:

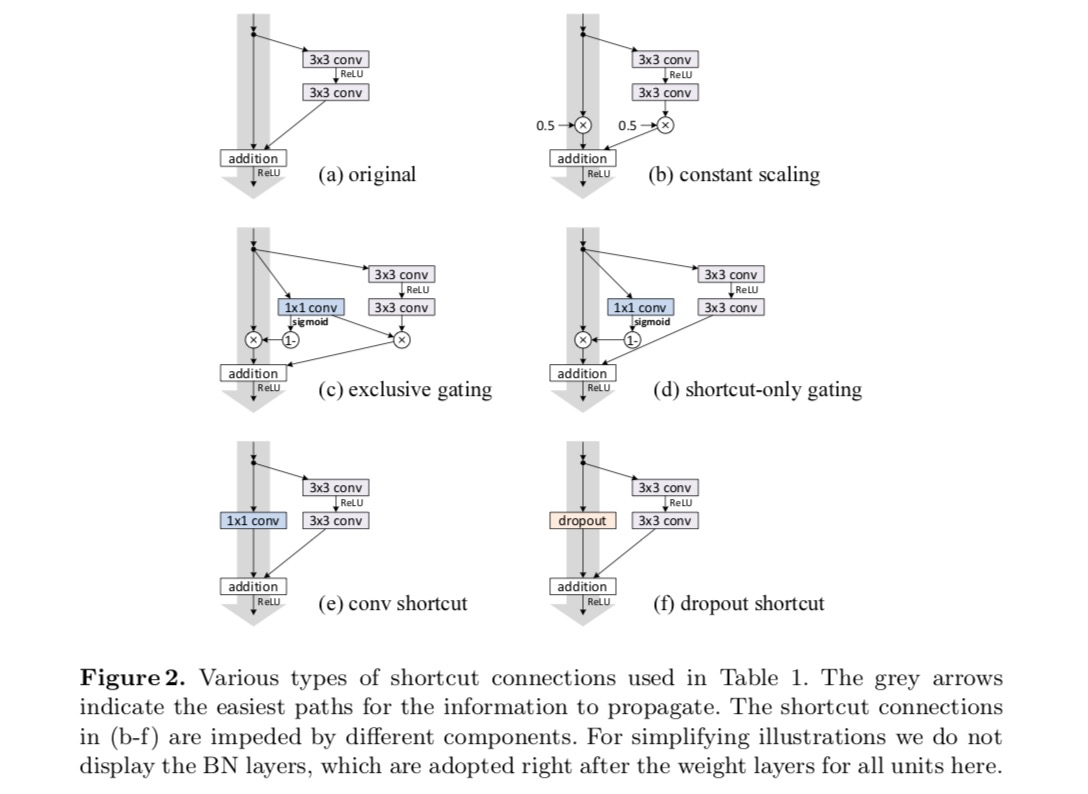
Os resultados da classificação são apresentados na tabela a seguir:

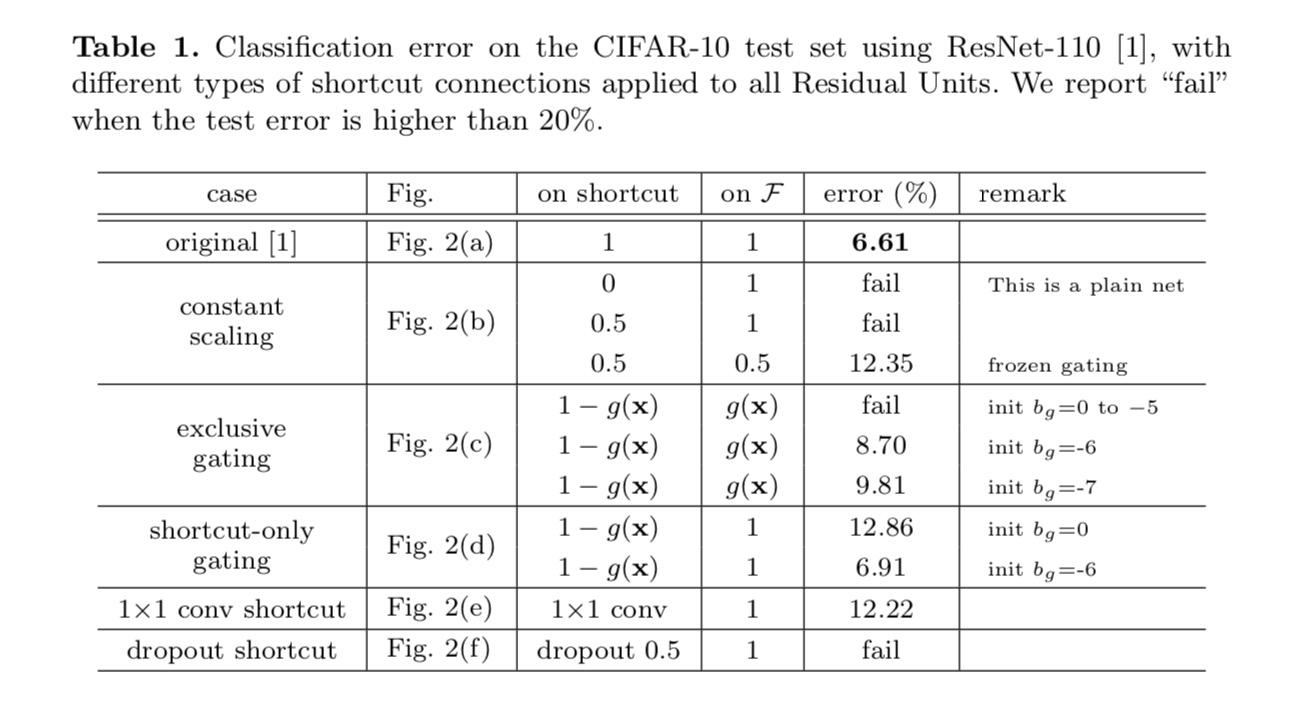
Conforme indicado pelas setas cinza na figura acima, as ligações de atalho são o caminho mais directo para a informação se propagar. Manipulações multiplicativas (escalamento, rotação, 1×1 convoluções, e desistência) nos atalhos podem dificultar a propagação da informação e levar a problemas de otimização.

é digno de nota que os atalhos convolucionais de Gate e 1×1 introduzem mais parâmetros, e devem ter habilidades de representação mais fortes do que os atalhos de identidade. Na verdade, o atalho-somente gating e convolução 1×1 cobrem o espaço de solução de atalhos de identidade (ou seja, eles podem ser otimizados como atalhos de identidade). No entanto, seu erro de treinamento é maior do que o dos atalhos de identidade, indicando que a degradação destes modelos é causada por questões de otimização, em vez de habilidades de representação.

o uso de funções de ativação

os experimentos na seção acima estão sob o pressuposto de que a ativação após adição é o mapeamento de identidade. Mas nos experimentos acima é ReLU como projetado no primeiro artigo. Em seguida, investigamos o impacto de .

queremos fazer um mapeamento de identidade, que é feito re-organizando as funções de ativação (ReLU e/ou BN, normalização em lote). Na figura seguinte, a unidade Residual original no último papel tem uma forma em Figo. 4 (A) – BN é usado após cada camada de peso, e ReLU é adotado após BN exceto que a última ReLU em uma unidade Residual é após adição elementar (=ReLU). Figo. 4 (b-e) mostram as alternativas que investigamos.

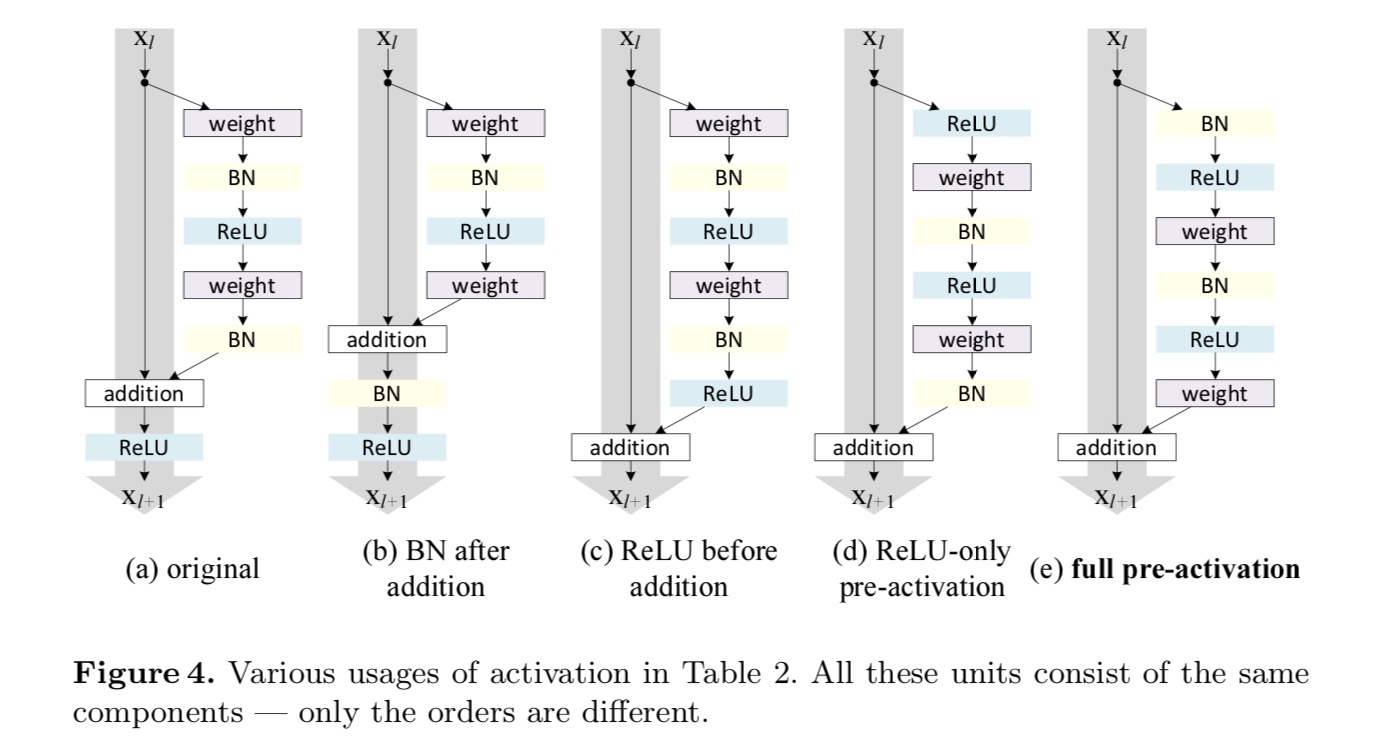
Experiments on Activation

in this section we experiment with ResNet-110 and a 164-layer Bottleneck architecture (denoted as ResNet-164). Uma unidade Residual de estrangulamento consiste numa camada de 1×1 para reduzir a dimensão, uma camada de 3×3 e uma camada de 1×1 para restaurar a dimensão. Como projetado no último artigo, sua complexidade computacional é semelhante à unidade Residual 2-3×3.pós-activação ou pré-activação?no projeto original, a ativação afeta ambos os caminhos na unidade Residual seguinte.: . Em seguida, desenvolvemos uma forma assimétrica onde uma ativação afeta apenas o caminho: , para qualquer um . Ao renomear as notações, temos a seguinte forma:

para esta nova unidade Residual como na equação acima, a nova ativação de pós-adição torna-se um mapeamento de identidade. Este projeto significa que, se uma nova ativação pós-adição é assimetricamente adotada, é equivalente à reformulação como a pré-ativação da unidade Residual seguinte. Isto é ilustrado na figura seguinte::

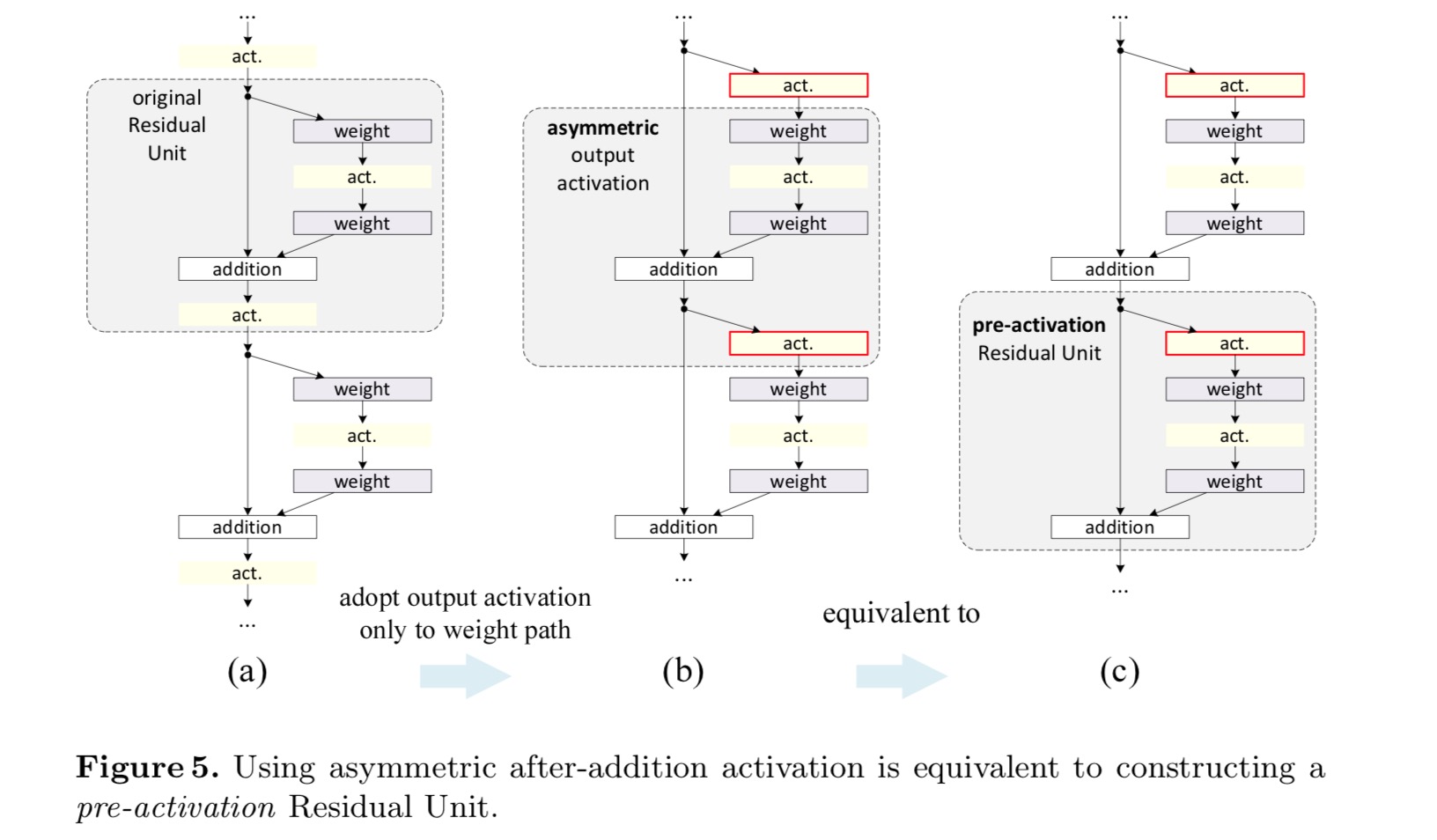
a distinção entre pós-activação / pré-activação é causada pela presença da adição em termos de elementos. Para uma rede simples que tem camadas N, há ativações n – 1 (BN/ReLU), e não importa se pensamos nelas como pós-ou pré-ativações. Mas para as camadas ramificadas fundidas por adição, a posição de ativação importa. Os vários usos da ativação são mostrados na Figura 4.nós experimentamos com dois desses projetos: (1) pré-ativação exclusivamente de ReLU e (2) pré-ativação completa em que BN e ReLU são adotados antes das camadas ponderais. De alguma forma, surpreendentemente, quando BN e ReLU são ambos utilizados como pré-ativação, os resultados são melhorados por margens saudáveis

achamos que o impacto da pré-ativação é duplo. Primeiro, a otimização é ainda mais facilitada (comparando com a ResNet de base) porque f é um mapeamento de identidade. Em segundo lugar, o uso do BN como pré-ativação melhora a regularização dos modelos.

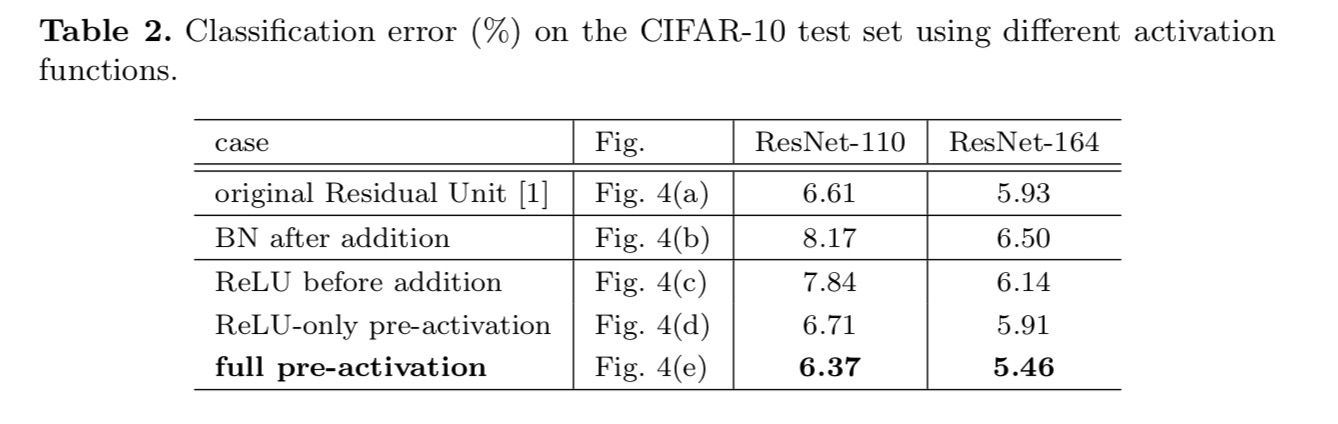
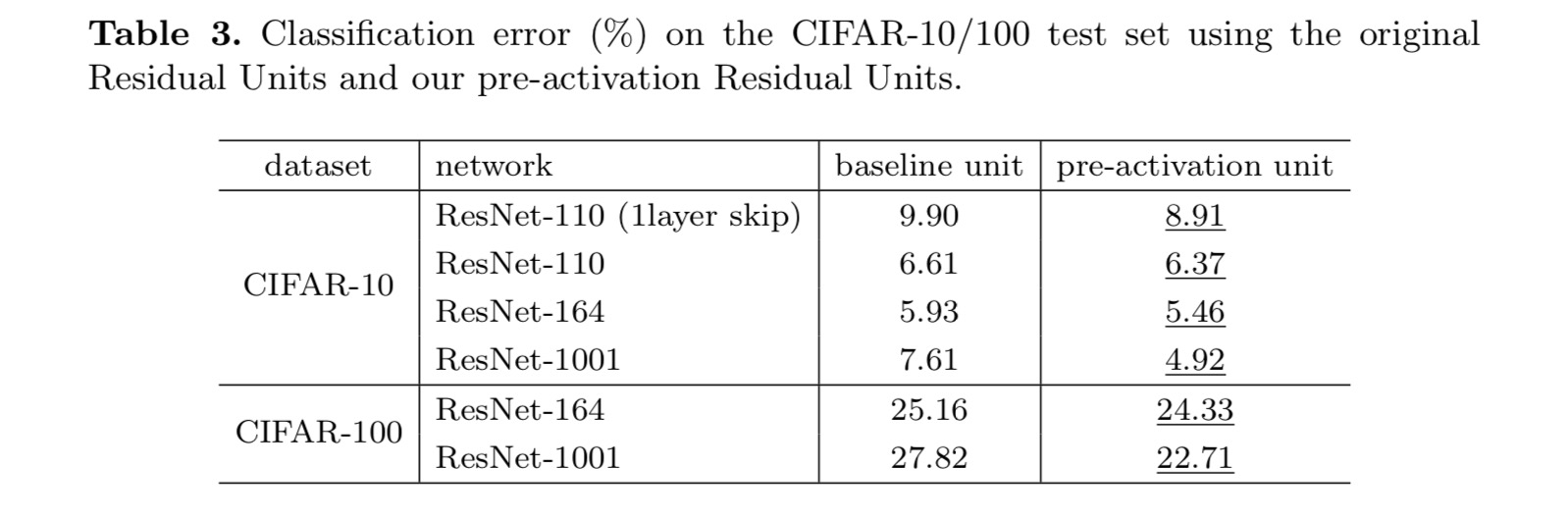
Conclusão

Este artigo investiga a propagação de formulações atrás da conexão de mecanismos de profunda residual redes. As nossas derivações implicam que as ligações de curto – circuito de identidade e a activação de pós-adição de identidade são essenciais para tornar a propagação da informação suave. Os experimentos de ablação demonstram fenomeneno que são consistentes com nossas derivações. Também apresentamos redes profundas de 1000 camadas que podem ser facilmente treinadas e alcançar maior precisão.

transformação Residual agregada para redes neurais profundas

introdução

a investigação sobre reconhecimento visual está a passar de “engenharia de recursos” para “engenharia de redes”. O esforço humano foi transferido para a concepção de melhores arquiteturas de rede para representações de aprendizagem.

projetar arquiteturas torna-se cada vez mais difícil com o crescente número de hiper-parâmetros, especialmente quando há muitas camadas. As redes VGG exibem uma estratégia simples, mas eficaz, de construir redes muito profundas: empilhar blocos de construção da mesma forma. Esta estratégia é herdada por ResNets que empilham módulos da mesma topologia. Esta regra simples reduz as escolhas livres de parâmetros hiper, e a profundidade é exposta como uma dimensão essencial nas redes neurais. Além disso, argumentamos que a simplicidade desta regra pode reduzir o risco de sobre-adaptar os hiper-parâmetros a um conjunto de dados específico. A robustez das redes VGG e ResNets tem sido comprovada por várias tarefas de reconhecimento visual e por tarefas não visuais envolvendo fala e linguagem.ao contrário de VGG-nets, a família de modelos iniciais demonstraram que topologias cuidadosamente projetadas são capazes de alcançar precisão convincente com baixa complexidade teórica. Os modelos iniciais têm evoluído ao longo do tempo, mas uma propriedade comum importante é uma estratégia de separação-transformação-fusão. Em um módulo inicial, a entrada é dividida em algumas incorporações de menor dimensão (por 1×1 convoluções), transformadas por um conjunto de filtros especializados (3×3, 5×5, etc.), e fundido pela concatenação. O comportamento split-transform-merge dos módulos iniciais é esperado para abordar o poder de representação de camadas grandes e densas, mas em uma complexidade computacional consideravelmente menor.apesar da boa precisão, a realização de modelos iniciais tem sido acompanhada por uma série de fatores complicadores. Embora combinações cuidadosas destes componentes produzam excelentes receitas de rede neural, não é, em geral, claro como adaptar as arquiteturas iniciais a novos conjuntos de dados/tarefas, especialmente quando existem muitos fatores e hiper-parâmetros a serem projetados.

neste artigo, apresentamos uma arquitetura simples que adota a estratégia de repetição de camadas VGG/ResNets, enquanto explora a estratégia de fusão de transformação dividida de uma forma fácil e extensível. Um módulo em nossa rede realiza um conjunto de transformações, cada uma em uma incorporação de dimensão baixa, cujas saídas são agregadas por Soma. Buscamos uma simples realização desta ideia-as transformações a serem agregadas são todas da mesma topologia. Este design nos permite estender a qualquer grande número de transformações sem Projetos especializados.empiricamente demonstramos que as nossas transformações agregadas superam o módulo original da ResNet, mesmo sob a condição restrita de manter a complexidade computacional e o tamanho do modelo. Enfatizamos que, embora seja relativamente fácil aumentar a precisão aumentando a capacidade (indo mais fundo ou mais largo), métodos que aumentam a precisão mantendo (ou reduzindo) a complexidade são raros na literatura.o nosso método indica que a cardinalidade (o tamanho do conjunto de transformações) é uma dimensão concreta e mensurável de importância central, além das dimensões de largura e profundidade. Experimentos demonstram que o aumento da cardinalidade é uma maneira mais eficaz de ganhar precisão do que ir mais fundo ou mais largo, especialmente quando a profundidade e largura começam a dar retornos decrescentes para os modelos existentes.

nossas redes neurais, chamadas de ResNeXt (sugerindo a próxima dimensão), superam ResNet-101/152, ResNet-200, Inception-v3, e Inception-ResNet-v2 no conjunto de dados de classificação do ImageNet. Em particular, um ResNeXt de 101 camadas é capaz de alcançar melhor precisão do que o ResNet-200, mas tem apenas 50% de complexidade. Além disso, a ResNeXt exibe projetos consideravelmente mais simples do que todos os modelos iniciais.

método

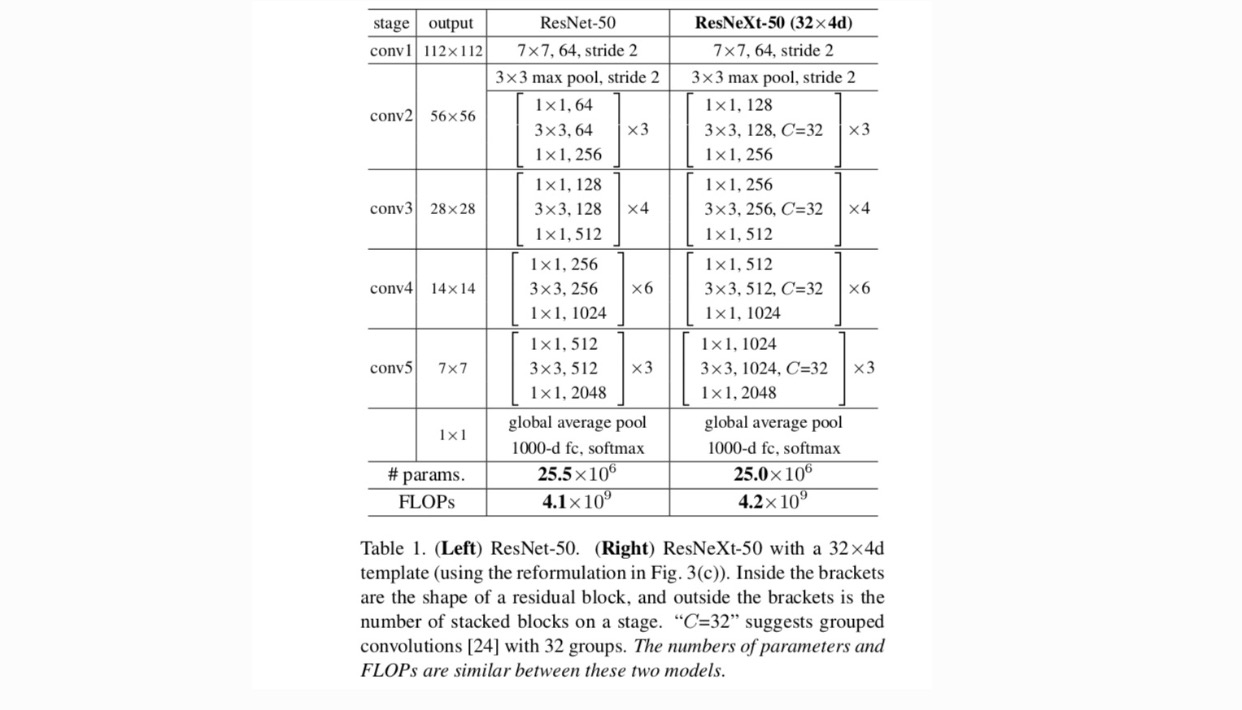
adotamos um projeto altamente modularizado seguindo VGG / ResNets. A nossa rede consiste numa pilha de blocos residuais. Estes blocos têm a mesma topologia, e estão sujeitos a duas regras simples inspirado VGG/ResNets: (1) se a produção de mapas espaciais do mesmo tamanho, os blocos de compartilhar o mesmo hiper-parâmetros (largura de filtro e tamanhos), e (2) cada vez que um mapa espacial é downsampled por um fator de 2, a largura dos blocos é multiplicado por um fator de 2. A segunda regra garante que a complexidade computacional, em termos de FLOPs (operações de ponto flutuante, em #of multiply-adds), é aproximadamente a mesma para todos os blocos.

com estas duas regras, nós só precisamos projetar um módulo modelo, e todos os módulos em uma rede podem ser determinados em conformidade. Então essas duas regras restringem muito o espaço de design e nos permitem focar em alguns fatores-chave. As redes construídas segundo estas regras estão no quadro 1.

os neurónios mais simples nas redes neurais artificiais executam o produto interno (soma ponderada), que é a Transformação Elementar feita por camadas totalmente conectadas e convolucionais.

a operação acima pode ser reformulada como uma combinação de divisão, transformação e agregação. (1): Divisão: o vetor é cortada como um baixo-dimensional de incorporação, e, acima, é um subespaço de dimensão (2) Transformação: a baixa-dimensional representação é transformada, e no exemplo acima, ela é simplesmente a escala: (3) Agregação: as transformações em todos os mergulhos são agregados .

dada a análise acima de um neurônio simples, consideramos a substituição da Transformação Elementar (w_i, x_i) por uma função mais genérica, que em si também pode ser uma rede. Formalmente, apresentamos transformações agregadas como:

onde pode ser uma função arbitrária. Analogous to a simple neuron, should project into an (opcionalmente low-dimensional) embedding and then transform it.

referimo-nos como cardinalidade. está em uma posição semelhante a in, mas não precisa igual e pode ser um número arbitrário. Mostramos através de experiências que a cardinalidade é uma dimensão essencial e pode ser mais eficaz do que as dimensões de largura e profundidade.

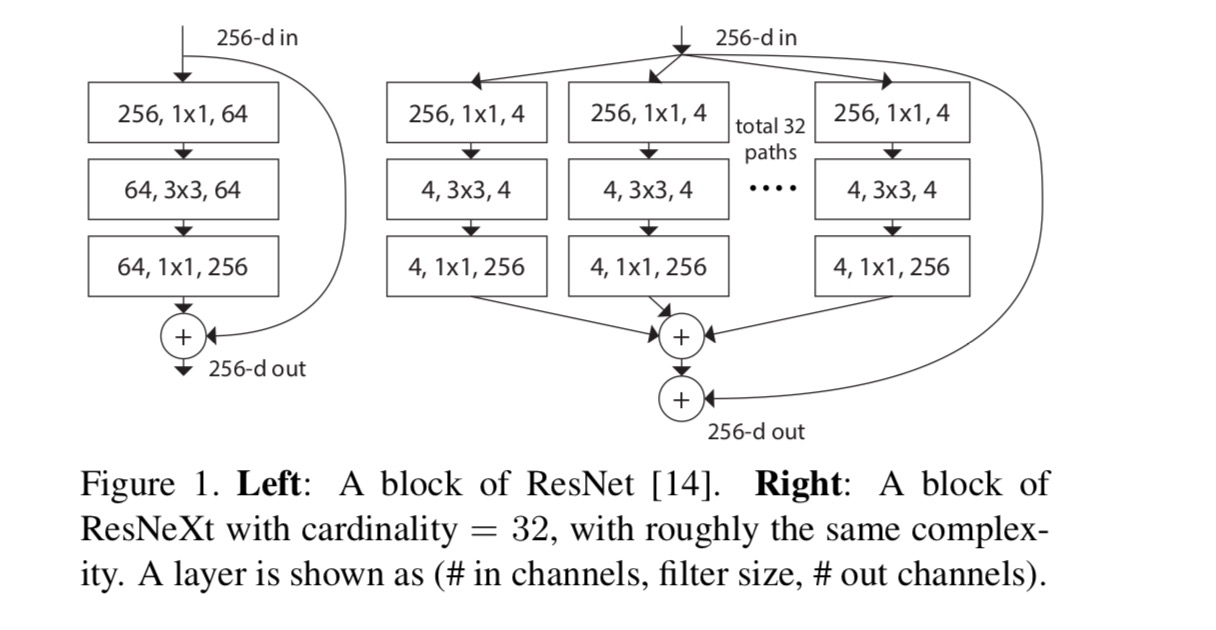
neste artigo, consideramos uma forma simples de desenhar as funções de transformação: todos têm a mesma topologia. Isto estende a estratégia do estilo VGG de repetir camadas da mesma forma. Nós definimos a transformação individual para ser a arquitetura em forma de gargalo ilustrada na Fig. 1 (direita). Neste caso, a primeira camada 1×1 em cada uma produz a incorporação de dimensões baixas.

a transformação agregada na última equação serve como função residual:

Onde está a saída.

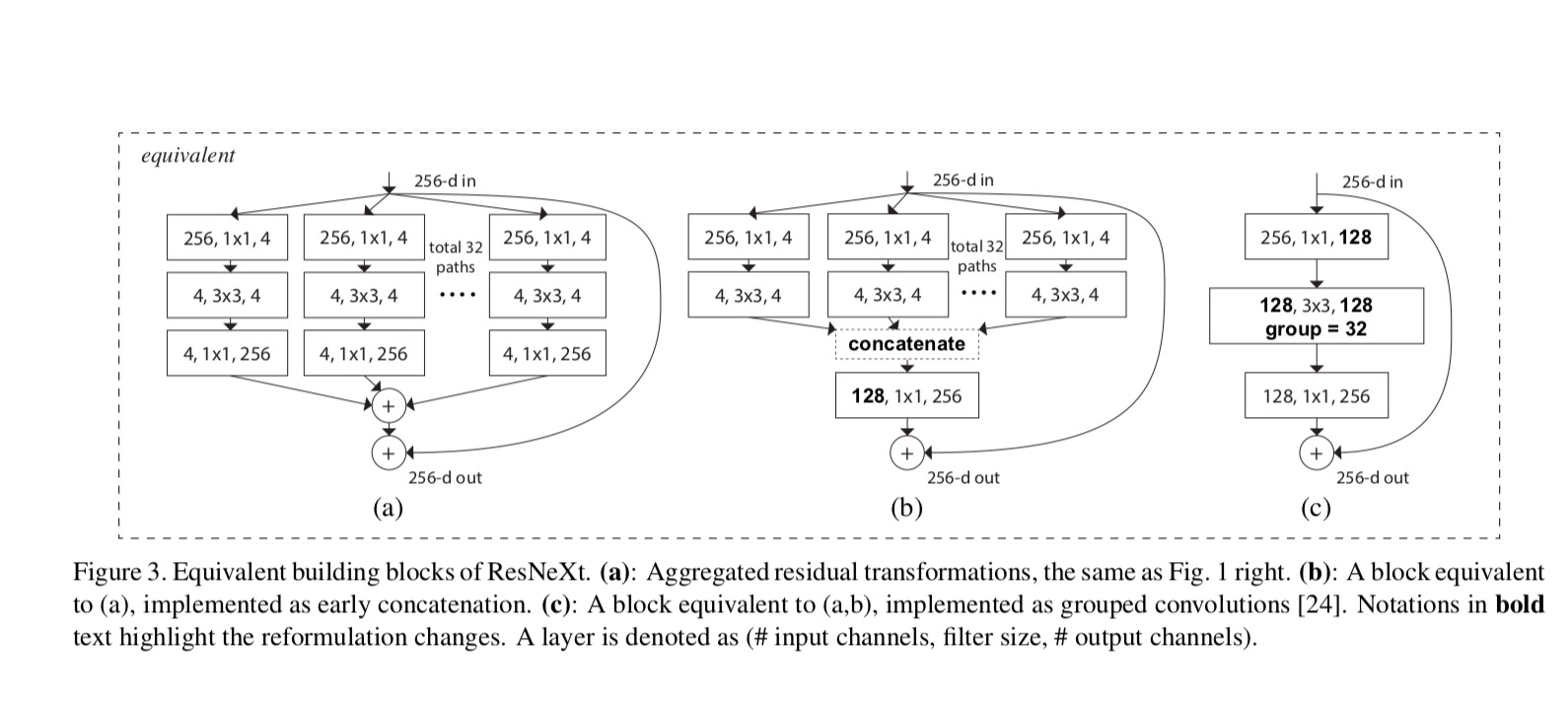
As relações entre ResNeXt e Inception-ResNet / Grouped-Convolutions são mostradas na figura seguinte:

Quando avaliamos diferentes cardinalities preservando a complexidade, queremos minimizar a modificação de outros hyper-parâmetros. Optamos por ajustar a largura do gargalo (por exemplo, 4-d Na Figura 1 (direita)), porque pode ser isolado a partir da entrada e saída do bloco. Esta estratégia não introduz alterações a outros hiper-parâmetros (profundidade ou largura de entrada/saída de blocos), por isso é útil para nos concentrarmos no impacto da cardinalidade.

na Fig. 1( à esquerda), o bloco de estrangulamento de ResNet original tem parâmetros e FLOPs proporcionais (no mesmo tamanho do mapa de recursos). Com a largura do gargalo, o nosso modelo na Fig. 1 (direita) tem: parâmetros e FLOPs proporcionais. Quando e, este número . A tabela seguinte mostra a relação entre a cardinalidade e a largura do gargalo .

Experiments

cardinalidade vs. largura. Primeiro avaliamos o trade-off entre cardinalidade e largura do gargalo, sob a complexidade preservada, conforme listado na Tabela 2. A tabela 3 mostra os resultados. Comparando com o ResNet-50, o 32×4d ResNeXt-50 tem um erro de validação de 22,2%, que é 1,7% menor do que a linha de base do ResNet 23,9%. Com a cardinalidade aumentando de 1 para 32, mantendo a complexidade, a taxa de erro continua a reduzir. Além disso, o ResNeXt 32×4d também tem um erro de treinamento muito menor do que o countetpart ResNet, sugerindo que os ganhos não são de regularização, mas de representações mais fortes.

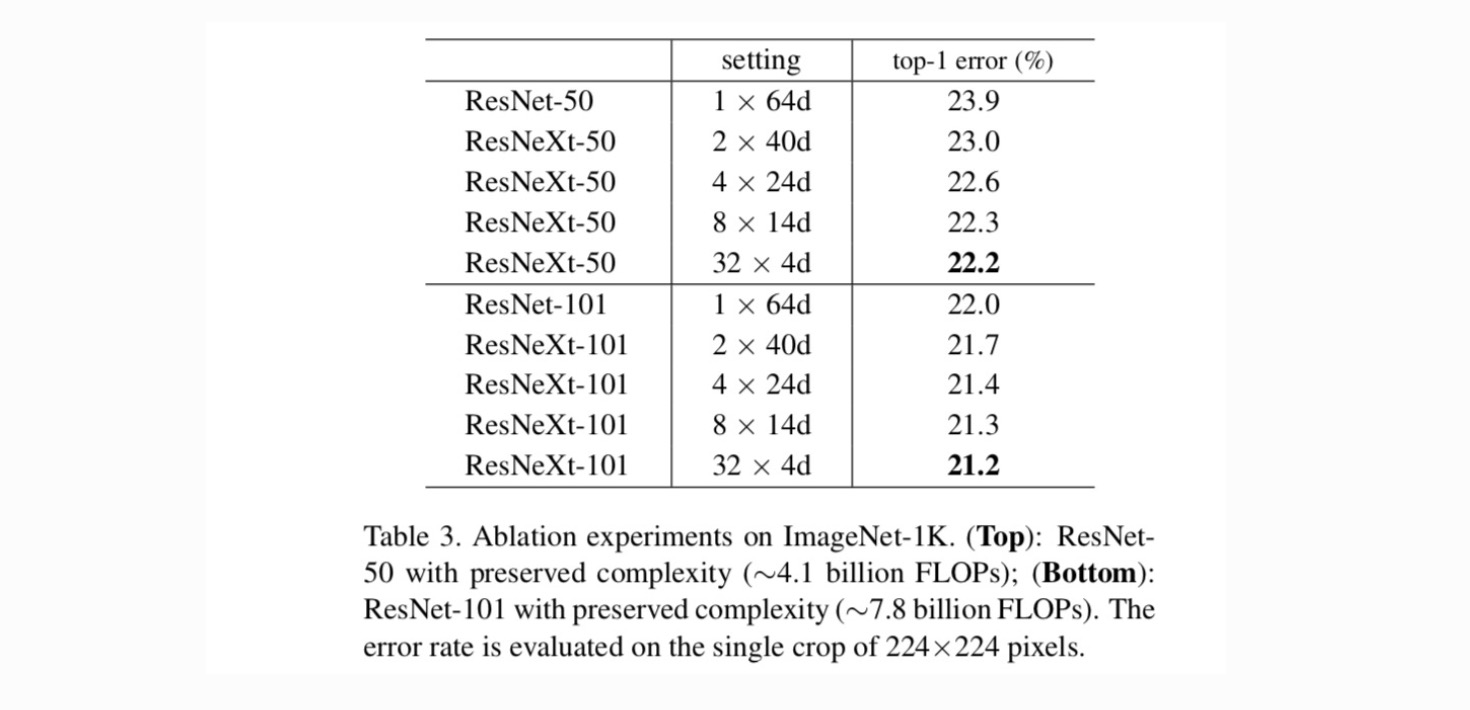
aumentando a cardinalidade vs. mais profunda / mais ampla.em seguida, investigamos o aumento da complexidade aumentando a cardinalidade C ou aumentando a profundidade ou largura. Comparamos as seguintes variantes (1) indo mais fundo para 200 camadas. Adoptamos a ResNet-200. (2) aumentando a largura do gargalo. (3) O aumento da cardinalidade duplicando C.

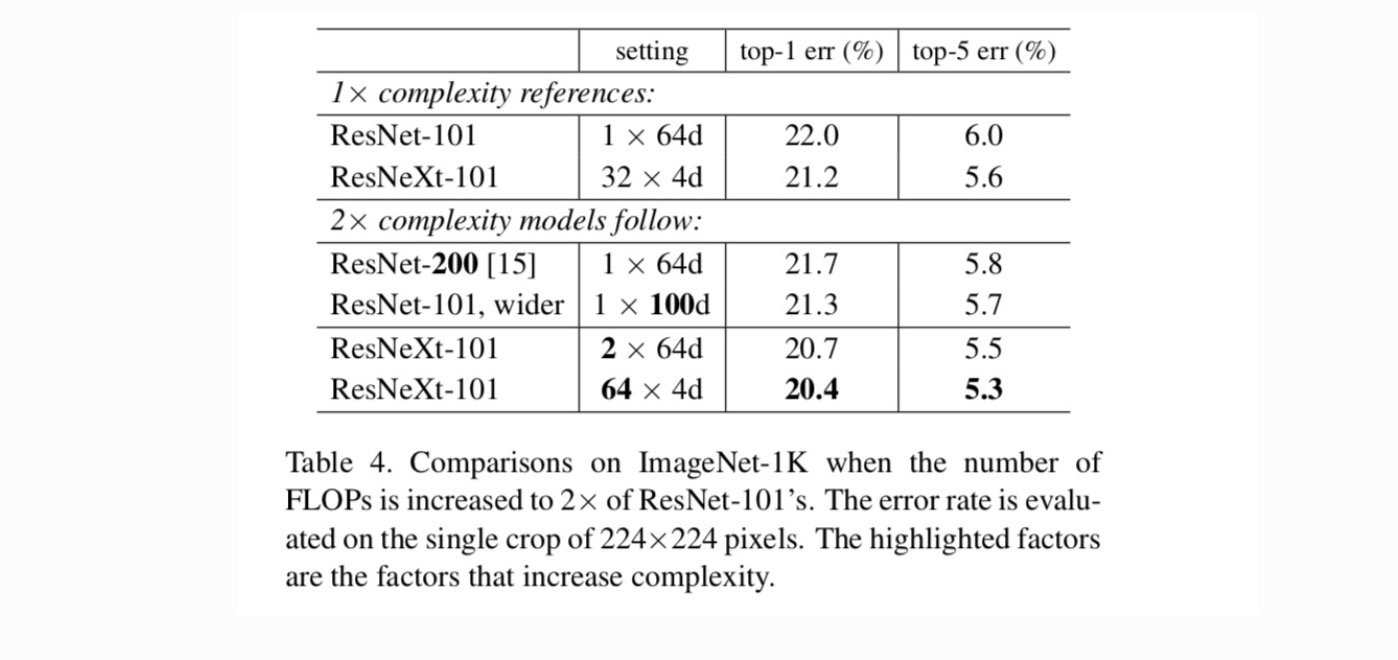
A Tabela 4 mostra que o aumento da complexidade em 2× reduz consistentemente o erro vs. A linha de base ResNet-101 (22, 0%). Mas a melhoria é pequena quando se vai mais fundo (ResNet-200, em 0,3%) ou maior (ResNet-101, em 0,7%). Pelo contrário, o aumento da cardinalidade C mostra resultados muito melhores do que ir mais fundo ou mais largo.

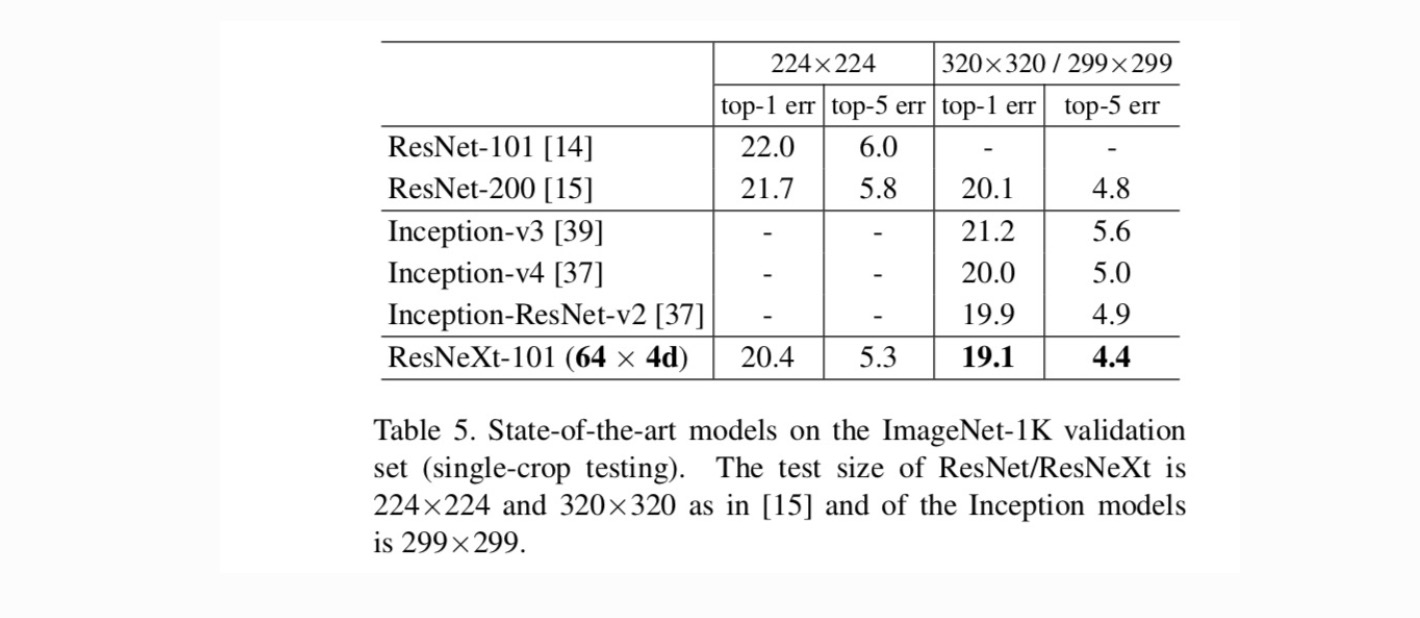
comparações com resultados de última geração. A tabela 5 mostra mais resultados de testes de monocultura no conjunto de validação ImageNet. Nossos resultados se comparam favoravelmente com ResNet, Inception-v3 / v4, e Inception-ResNet-v2, alcançando uma taxa de erro top-5 de 4,4%. Além disso, nosso design de arquitetura é muito mais simples do que todos os modelos iniciais, e requer consideravelmente menos hiper-parâmetros a serem definidos manualmente.