
Máquina de aprendizagem é, em última análise utilizado para predizer os resultados, dado um conjunto de recursos. Portanto, tudo o que podemos fazer para generalizar o desempenho do nosso modelo é visto como um ganho líquido. Dropout é uma técnica usada para evitar que um modelo se sobreponha. Dropout funciona definindo aleatoriamente as bordas de saída de unidades ocultas (neurônios que compõem camadas ocultas) para 0 em cada atualização da fase de treinamento. Se você der uma olhada na documentação de Keras para a camada dropout, você verá um link para um livro branco escrito por Geoffrey Hinton e amigos, que entra na teoria por trás do dropout.
o processo, por exemplo, nós vamos estar usando Keras para construir uma rede neural com o objetivo de reconhecer a escrita à mão dígitos.
from keras.datasets import mnist
from matplotlib import pyplot as plt
plt.style.use('dark_background')
from keras.models import Sequential
from keras.layers import Dense, Flatten, Activation, Dropout
from keras.utils import normalize, to_categorical
usamos Keras para importar os dados para o nosso programa. Os dados já estão divididos em conjuntos de treinamento e testes.
(X_train, y_train), (X_test, y_test) = mnist.load_data()
Let’s have a look to see what we’re working with.
plt.imshow(x_train, cmap = plt.cm.binary)
plt.show()

Depois que terminar de formação fora do modelo, ele deve ser capaz de reconhecer a anterior imagem como um de cinco.
Há um pouco de pré-processamento que devemos realizar de antemão. Normalizamos os pixels (recursos) de modo que eles variam de 0 a 1. Isto permitirá ao modelo convergir para uma solução muito mais rápida. Em seguida, transformamos cada uma das etiquetas de destino para uma dada amostra em uma matriz de 1s e 0s onde o índice do número 1 indica o dígito que a imagem representa. Fazemos isso porque, caso contrário, nosso modelo interpretaria o dígito 9 como tendo uma prioridade maior do que o número 3.
X_train = normalize(X_train, axis=1)
X_test = normalize(X_test, axis=1)
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
sem gota
Antes de alimentar uma matriz dimensional em uma rede neural, usamos uma camada plana que a transforma em uma matriz dimensional 1, adicionando cada linha subseqüente à que a precedeu. Vamos usar duas camadas ocultas que consistem em 128 neurônios cada e uma camada de saída que consiste em 10 neurônios, cada um para um dos 10 possíveis dígitos. A função de ativação de softmax retornará a probabilidade de uma amostra representar um dado dígito.

Já que estamos tentando prever classes, nós usamos categórica crossentropy como a nossa perda de função. Vamos medir o desempenho do modelo com precisão.
model.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=
)
reservamos 10% dos dados para validação. Vamos usar isso para comparar a tendência de um modelo para exagerar com e sem desistência. Um tamanho de lote de 32 implica que iremos calcular o gradiente e dar um passo na direção do gradiente, com uma magnitude igual à velocidade de aprendizagem, depois de passar 32 amostras através da rede neural. Fazemos isso um total de 10 vezes conforme especificado pelo número de epochs.
history = model.fit(
X_train,
y_train,
epochs=10,
batch_size=32,
validation_split=0.1,
verbose = 1,
shuffle=True
)

Nós podemos plotar o treinamento e a validação de precisão, em cada época, utilizando a história da variável retornada pela função ajuste.
Como pode ver, sem desistência, a perda de validação pára de diminuir após a terceira época.

As you can see, without dropout, the validation accuracy tends to plateau around the third epoch.

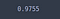
Using this simple model, we still managed to obtain an accuracy of over 97%.
test_loss, test_acc = model.evaluate(X_test, y_test)
test_acc
Dropout
Há algum debate sobre se a desistência deve ser colocado antes ou depois da função de ativação. Como regra geral, coloque a gota após a função de ativação para todas as funções de ativação, exceto relu. De passagem 0,5, cada unidade oculta (neurônio) é definida para 0 com uma probabilidade de 0,5. Em outras palavras, há uma mudança de 50% que a saída de um determinado neurônio será forçada a 0.

de Novo, já que estamos tentando prever classes, nós usamos categórica crossentropy como a nossa perda de função.
model_dropout.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=
)
ao fornecer o parâmetro de divisão de validações, o modelo irá separar uma fração dos dados de treinamento e irá avaliar a perda e qualquer métrica modelo sobre estes dados no final de cada época. Se a premissa por trás do dropout se mantiver, então devemos ver uma diferença notável na precisão de validação em comparação com o modelo anterior. O parâmetro shuffle irá baralhar os dados de treinamento antes de cada época.
history_dropout = model_dropout.fit(
X_train,
y_train,
epochs=10,
batch_size=32,
validation_split=0.1,
verbose = 1,
shuffle=True
)

Como você pode ver, a validação de perda é significativamente menor do que a obtida com o modelo regular.

Como você pode ver, o modelo convergente muito mais rápido e obteve uma precisão de cerca de 98% na validação do conjunto, considerando que o modelo anterior estabilizou em torno da terceira época.

A precisão obtida no conjunto de teste não é muito diferente do que o obtido a partir do modelo sem a evasão escolar. Isto deve-se muito provavelmente ao número limitado de amostras.
test_loss, test_acc = model_dropout.evaluate(X_test, y_test)
test_acc

considerações Finais
de Eliminação pode ajudar um modelo de generalizar por acaso configuração de saída para um dado neurônio a 0. Ao definir a saída para 0, a função de custo torna-se mais sensível aos neurônios vizinhos mudando a forma como os pesos serão atualizados durante o processo de backpropagação.