Posted June 2008.
a segunda de duas colunas sobre a matemática da topografia (a primeira é aqui). …
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
John Eggers
University of California, San Diego
jeggers at ucsd.edu
 e-Mail para um amigo e-Mail para um amigo |
 Imprimir este artigo Imprimir este artigo |
Um planimeter é uma tabela-top instrumento para medir áreas, geralmente as áreas irregulares regiões em um mapa ou fotografia. Eles já foram comuns, mas agora em grande parte foram substituídos por ferramentas digitais.
A imagem seguinte dá alguma ideia da configuração. O braço do Pólo gira livremente em torno do Pólo, que é fixado na mesa. O braço tracer gira em torno do pivô, que é onde ele se junta ao braço polar. Trace-se uma curva no sentido horário com o marcador, e ao fazê-lo a roda de medição desloca-se, e a distância total que rola é acumulada no mostrador. A roda de apoio impede a coisa de cair. No final, você lê um número do mostrador, e depois da multiplicação por um fator dependendo apenas da configuração particular do planímetro, você obtém a área dentro da curva.

A figura seguinte dá-lhe uma melhor visão do mecanismo.

chamamos o transporte de conjunto de rodas, dial e pivô. Na próxima imagem, você pode olhar melhor para ele, e pode ver o worm drive que faz com que o dial para girar à medida que a roda de medição se move.

Aqui está o diagrama do original planimeter, a partir do artigo de Jakob Amsler que o introduziu:
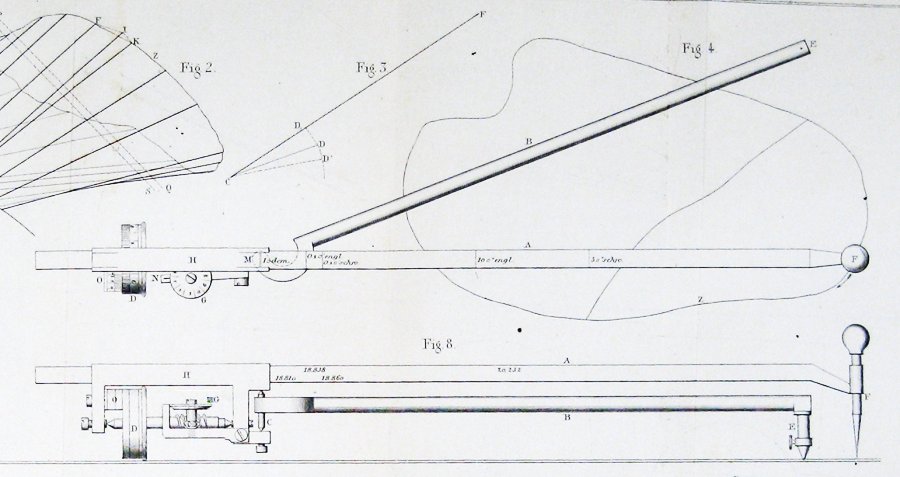
Como pode uma coisa tão simples de medir áreas?
geometria do planímetro
o movimento no Sentido DOS ponteiros do relógio do planímetro é a direção oposta ao que matemáticos decidiram ser rotação positiva. Em vez de violar esta convenção, vamos trabalhar a partir de agora com o planímetro de um matemático, no qual você se move no sentido contrário ao dos ponteiros do relógio. Como as fantasias de outros matemáticos, não há nenhuma no planeta!
Existem algumas restrições sobre como colocar o planímetro em relação à curva que você quer traçar. A carruagem pode ser deslizada ao longo do braço tracer, mas em todos os casos o comprimento l do braço tracer é menor do que o comprimento r do braço do poste. Isso significa que o rastreador nunca pode chegar a uma distância r – l do Polo. Por outro lado, quando é completamente estendido, o rastreador nunca pode chegar além de r + L. assim, a curva a ser traçada deve estar dentro do anulus entre dois círculos, um com raio r – l, O Outro r + L.

na verdade, deve tornar-se claro em um momento que os braços nunca devem ser completamente estendidos, de modo que a curva a ser traçada deve estar completamente dentro do anulo. Além disso, normalmente o pólo é colocado no exterior da curva.

para um dado ponto no anulo, existem exatamente duas configurações possíveis do planímetro que colocam o marcador nesse ponto. Escolher um ponto ou o outro significa escolher um sinal para uma raiz quadrada. Chamamos a isto escolher uma orientação para o planímetro. É positivo se a raiz quadrada for positiva. Uma vez que uma orientação tenha sido escolhida, ela permanecerá a mesma, a menos que o braço seja completamente estendido. Isto nunca deve acontecer. Enquanto a sua curva estiver inteiramente dentro do annulus, as configurações do planímetro variarão suave e unicamente com o caminho do tracer.
a próxima coisa a fazer é entender algumas coisas sobre o movimento da roda de medição. Como mostra a figura seguinte, se a roda viaja em linha recta a uma distância C, a roda gira através de um ângulo θ = c/R em que R é o seu raio.

portanto, é realmente verdade que a rotação da roda e a distância percorrida pelo braço marcador têm alguma relação entre si. Mas esta relação é um pouco subtil. Se o braço apenas se move em frente a uma distância C, a área varrida será lC, mas se ele se desloca paralelamente a si mesmo a área varrida será 0. No primeiro caso, um ponto na circunferência da roda irá mover a distância C. No segundo caso, a roda não se moverá de todo. E se o braço se traduz obliquamente, a roda girará uma distância igual à altitude do paralelogramo coberto pelo braço. Em todos os casos em que o braço se traduz paralelamente a si próprio, a área varrida pela porção do braço marcador entre o pivô e o marcador será igual a lC, em que C é a distância medida pela rotação da roda. Este é o fato básico que relaciona o movimento do braço ao movimento da roda de medição.

O caminho para a frase esta, precisamente, é que não importa como o braço move-se, a distância medida pela roda é o caminho integral

onde Γ é o caminho percorrido pelo ponto de braço, onde a roda de medição é ligado, n é o vetor unitário perpendicular ao braço, a qualquer momento, e t é o vetor unitário apontando na direção de viagem (de modo que, por exemplo, se o braço está em movimento paralelo a si mesmo o produto escalar de n e t é 0).
Teorema de Guldin
em seguida, vamos tentar tornar o comportamento do planímetro intuitivamente claro, mas primeiro vamos olhar para um tipo especial de planímetro, e neste caso provar um resultado mais geral. Suponha que pegamos um único braço livremente em movimento de comprimento l e anexamos a ele uma roda de medição de raio R direita em seu centro.

Depois movemos o braço em torno do plano. Se a roda de medição rodar através de um ângulo total de θ radianos à medida que o braço se move, a distância a que um ponto da circunferência se desloca é C = θR.
Teorema de Guldin. Nesta situação, a área total varrida pelo braço é o produto lC.
A Área aqui é interpretada com um sinal. Se o braço apenas gira em torno de seu centro, uma metade do braço vai para a frente e a outra para trás, e os dois cancelam.
já vimos que a afirmação de Guldin é válida no caso de o braço apenas traduzir. Claro que isso nem sempre acontece – o braço pode rodar como se move, bem como traduzir. Mas podemos ver o que está a acontecer cortando a área varrida da seguinte forma::

porque a roda de medição está no centro do braço, à medida que o braço gira, esmaga os blocos pequenos de um lado à medida que os expande no outro. Estes efeitos anulam-se exactamente.
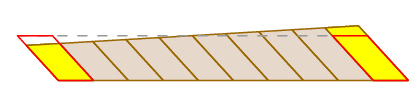
uma prova completamente rigorosa pode ser dada usando a fórmula para a mudança de variáveis em uma integral dupla e a expressão para o curso da roda como uma integral do caminho.agora suponha que a roda está colocada em outro lugar. Digamos que sua posição é c + v onde c é o centro do braço, e v um vetor ao longo do braço. O comprimento de v permanecerá fixo, por exemplo, em ρ. O percurso que a roda segue é c (t) + v(t). O caminho integral é agora
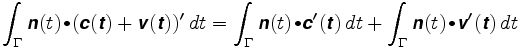
A primeira integral é a distância que a roda iria viajar se fosse o centro do braço. No segundo, o vetor v (t) é sempre perpendicular a n, e v(t) tem comprimento constante. O vector v (t) move-se em torno de um círculo de raio igual a ρ. Portanto, o produto Ponto de N E v'(t) é apenas o comprimento assinado de v'(t), e a segunda integral é igual a ρ vezes a rotação total do braço. Assim:se a roda estiver à distância ρ do centro do braço, a distância C mede C0 , a distância que seria medida se a roda estivesse no centro, Mais ρ vezes o ângulo total θ Que o braço gira.
Você pode ver imediatamente um caso simples disto girando o braço em torno de seu centro. Combinando isto com o teorema de Guldin, vemos que em todos os casos:
C = C0 + ρ θ
área varrida = l C0 = l C – L ρ θ
o resultado completo
a fórmula de Guldin dá uma área assinada-se você varrer para trás sobre uma área, a roda vai para trás e você cancela a área que já cobriu. Se aplicarmos isto ao caso em que o braço livre volta exatamente para onde começou, vemos que lC é igual à área da região fechada traçada pela extremidade direita do braço menos a da região varrida pela esquerda.
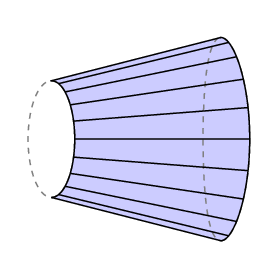
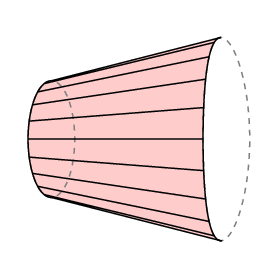

No caso do urso polar planimeter, a parte inferior do braço é restrito a um arco do círculo de raio r com centro no pólo, daí l C é a área traçada pelo marcador. Além disso, normalmente o Polo fica fora da região a ser medida, e neste caso a quantidade total de rotação do braço tem que ser 0. Portanto, neste caso, temos
Área da região rastreada = lC
Aqui está a figura incluído por Jakob Amsler, o inventor, em seu original, em papel no aparelho que ele inventou:
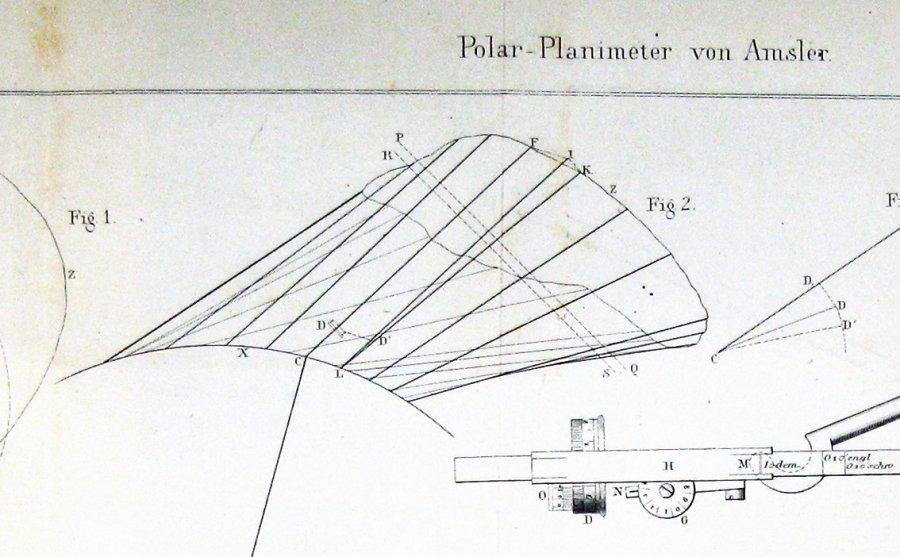
parece muito claro que Amsler derivado de sua construção através de alguma forma de teorema de Guldin.
planímetros e Teorema de Green
como já mencionamos, tendo escolhido a orientação do planímetro, a configuração do planímetro é uma função contínua da posição do marcador. Digamos que escolhemos a orientação positiva. Então podemos anexar a cada ponto do anulo um vetor unitário n, o que aponta no sentido contrário aos ponteiros do relógio e perpendicular ao braço do tracer no tracer.
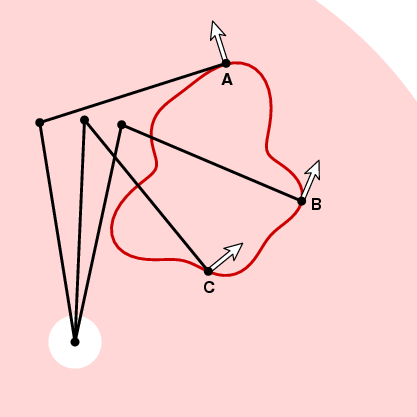
Como a roda de medição vai responder de movimento ao longo da curva no instante seguinte depende do ângulo entre este vetor e a unidade de vetor tangente da curva. Em um na figura acima, a roda de medição não vai se mover porque o movimento ao longo da curva é paralelo ao braço tracer. Em B Se o localizador mover uma pequena distância ds, assim como a roda de medição. E em C a roda de medição irá mover alguma distância entre 0 e ds. Para ser preciso, suponha que t é o vetor tangente unitário em algum ponto da curva. Se o localizador mover a distância ds ao longo da curva, nesse ponto a roda de medição irá mover uma distância d D ds, onde d = N. t, o produto Ponto dos vetores unitários t e N. em outras palavras, se nos movermos em torno da curva Γ a roda de medição irá mover uma distância total igual à integral de N. t ds (produto escalar), ou

Mas, uma vez que cada ponto do anel corresponde a um único positivo de configuração do planimeter, podemos atribuir um vetor de n para cada ponto interior do anel, e, portanto, define um campo de vetores. A curva Γ é o limite de seu interior Ω, e por uma de nossas suposições isto está contido inteiramente na região onde n é definido. O teorema de Green nos diz que a integral do caminho em torno do limite desta região também é igual a uma certa integral sobre Ω: Portanto
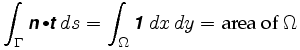
Mais precisamente, Verde Teorema de nos dizer que
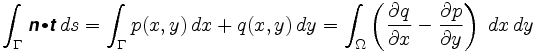
, onde n = é o vetor de campo envolvidos. O integrand na integral dupla é chamado de curva do campo vetorial.
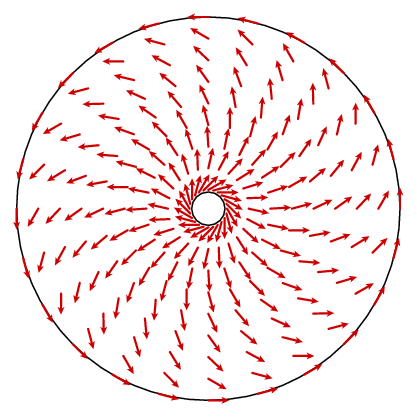
isto não nos parece levar muito longe. O que deve acontecer é que o curl é uma constante 1. Em princípio, poderíamos encontrar uma fórmula para o campo vetorial n e calcular sua curva, mas isso não é muito esclarecedor. No entanto, podemos tirar partido de outro facto. O campo vetorial tem simetria circular, o que significa que é determinado pelo que é em um raio. A lei Cosina nos dá uma fórmula simples para o componente circunferencial.
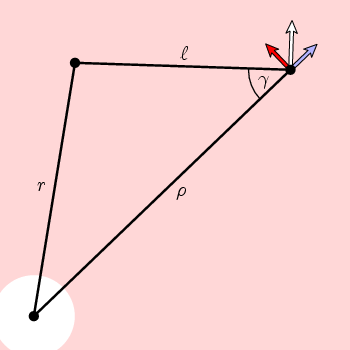
segue de geometria simples nesta figura que o circunferencial componente de n é
f(ρ) = cos(γ) = (ρ 2 + l 2 – r 2)/(2 ρ l)
O real ponto de Green Teorema é que, a fim de verificar que o integrando é 1, é suficiente para verificar que o caminho integral de todo adequado pequenos caminhos é a mesma área. Para isso, escolhemos as nossas regiões como aqui:
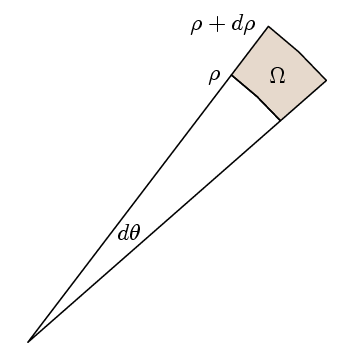
em Seguida, l vezes o caminho integral é
l (ρ+dp)( f(ρ+dp)- f(ρ) ) dθ
ou
(θ/2) ( (ρ + dp) 2 – ρ 2)
qual é a área da região Ω.
Outros tipos de planimeters
o Teorema de Guldin implica que o movimento de uma roda de medição vai contar a área traçada pelo tracer sempre o braço com uma roda de medição em traça uma curva, mas tem um final restrito a um one-dimensional curva. Isto acontece, por exemplo, com o planímetro de rolamento, no qual o pivô é restrito a uma linha reta por estar em um cilindro rolante.

Para saber mais
-
 ainda faz e vende planimeters.
ainda faz e vende planimeters. - Cálculo Diferencial e Integral Volume II, R. Courant, Blackie & Son, 1936. A seção sobre a fórmula de Guldin (pp. 294-298) oferece uma explicação de como o planímetro funciona.o artigo original de Amsler, Vierteljahresschrift der Naturforschenden Gesellschaft in Zuerich, 1856. Isso é falta de diagramas, mas eles estão aqui:
- Amsler primeiro diagrama
- Amsler segundo diagrama
os Nossos agradecimentos a Donna Sammis da Stony Brook University Library para localizar o artigo e seu marido, Robert para o fornecimento de fotografias das figuras.
A empresa que Amsler fundou produziu instrumentos bem no século XX. Esta fotografia mostra o logótipo, numa versão do pantógrafo do planímetro:

- ” sobre os planímetros, ” EngineerSupply. A empresa também postou um vídeo no YouTube.
projeto de lei Casselman
Universidade de British Columbia, Vancouver, Canadá
cass em matemática.a ubc.ac
João Eggers
Universidade da Califórnia, em San Diego
em jeggers ucsd.edu
quem pode acessar o MEE pode encontrar alguns dos trabalhos mencionados acima. Para aqueles com acesso, o MathSciNet da American Mathematical Society pode ser usado para obter informações bibliográficas adicionais e revisões de alguns destes materiais. Alguns dos itens acima podem ser acessados através do Portal ACM , que também fornece serviços bibliográficos.