
Uma Rede Neural Artificial (ANN) é feito de muitos neurônios interconectados:
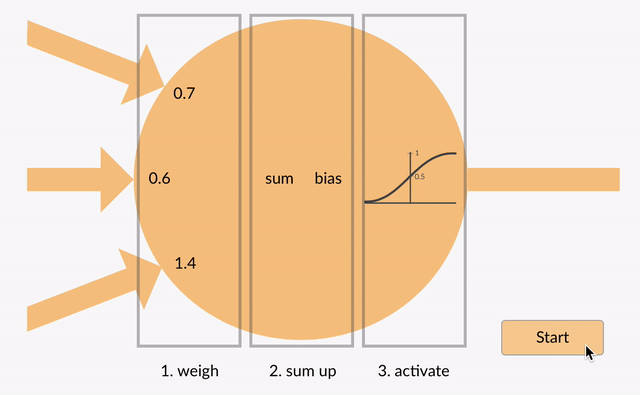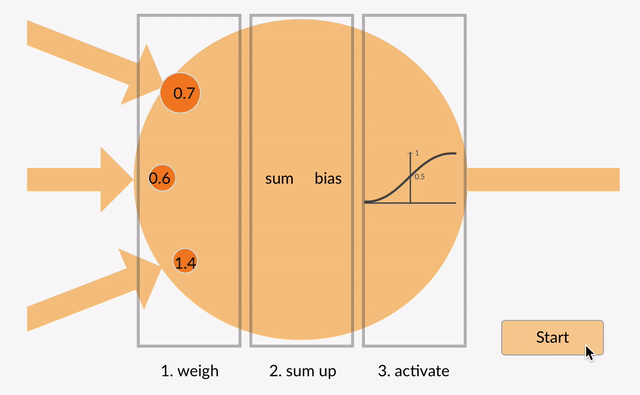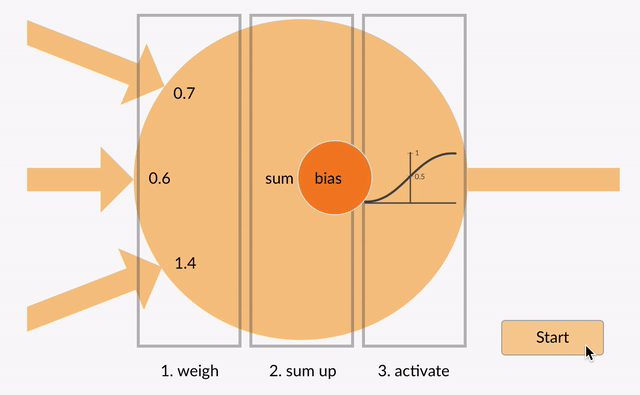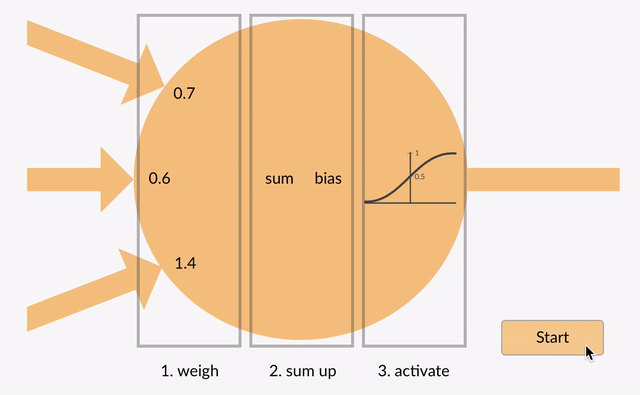
Cada neurônio leva em alguns números em ponto flutuante (por exemplo, 1.0, 0.5, -1.0) e multiplica – os por outros números de vírgula flutuante (por exemplo, 0.7, 0.6, 1.4) conhecidos como pesos.(1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Os pesos agem como um mecanismo para focar, ou ignorar, certas entradas.

ponderado entradas, em seguida, obter convocados (por exemplo, 0.7 + 0.3 + -1.4 = -0.4) juntamente com um valor de enviesamento (por exemplo-0.4 + – 0.1 = – 0.5).
O valor somado (x) é agora transformado em um valor de saída (y) de acordo com a função de ativação do neurônio (y = f(x)). Alguns populares ativação de funções são mostradas a seguir:

e.g. -0.5 → -0.05 se usar o Vazamento Rectificado Unidade Linear (Leaky ReLU) função de ativação: y = f(x) = f(-0.5) = max(0.1*-0.5, -0.5) = max(-0.05, -0.5) = -0.05
o valor de saída do neurônio (por exemplo, -05) é frequentemente uma entrada para outro neurônio.
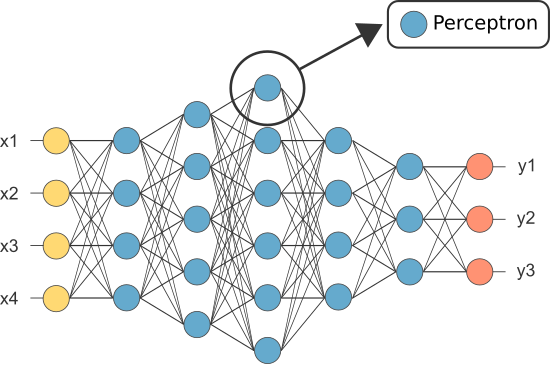
no Entanto, um dos primeiros ANNs era conhecido como o perceptron e é composta de apenas um único neurônio.

A saída do perceptron é (apenas) do neurônio atua como a previsão final.

Permite que o código de nossa própria Perceptron:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(Nota: não incluímos qualquer algoritmo de aprendizagem, em nosso exemplo acima — abordaremos os algoritmos de aprendizagem em outro tutorial)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

so why do we need so many neurons in an ANN if any one will suffer (as a classifier)?

Infelizmente, neurônios individuais só são capazes de classificar linearmente separáveis de dados.

no Entanto, através da combinação de neurônios juntos, nós essencialmente combinar a sua decisão limites. Portanto, uma ANN composta por muitos neurônios é capaz de aprender limites de decisão complexos e não lineares.

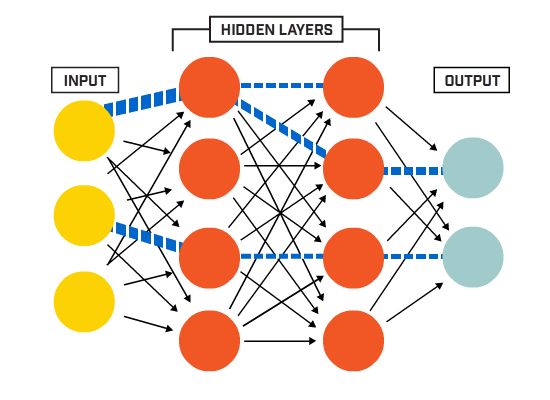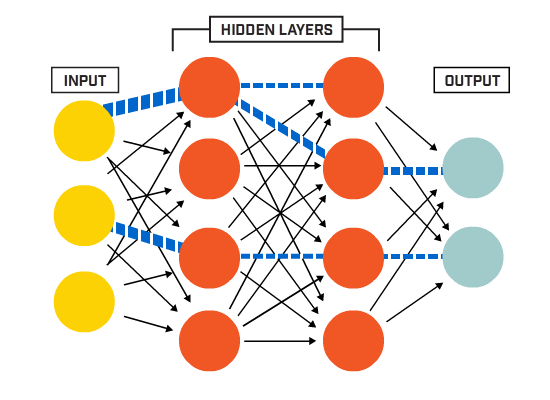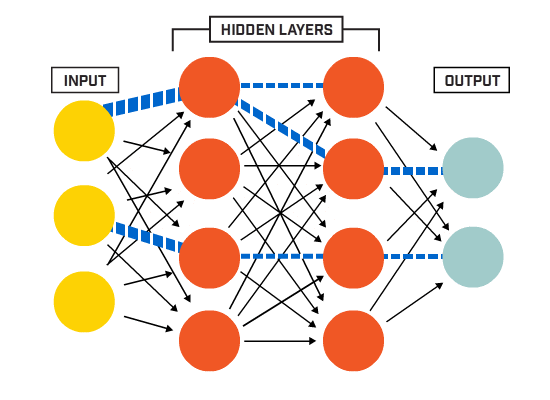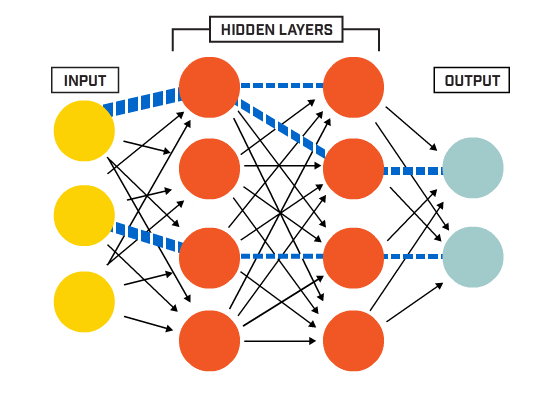
os Neurónios estão conectados entre si de acordo com uma rede específica de arquitetura. Embora haja arquiteturas diferentes, quase todas contêm camadas. (NB:: Neurônios da mesma camada não se conectar com o outro)
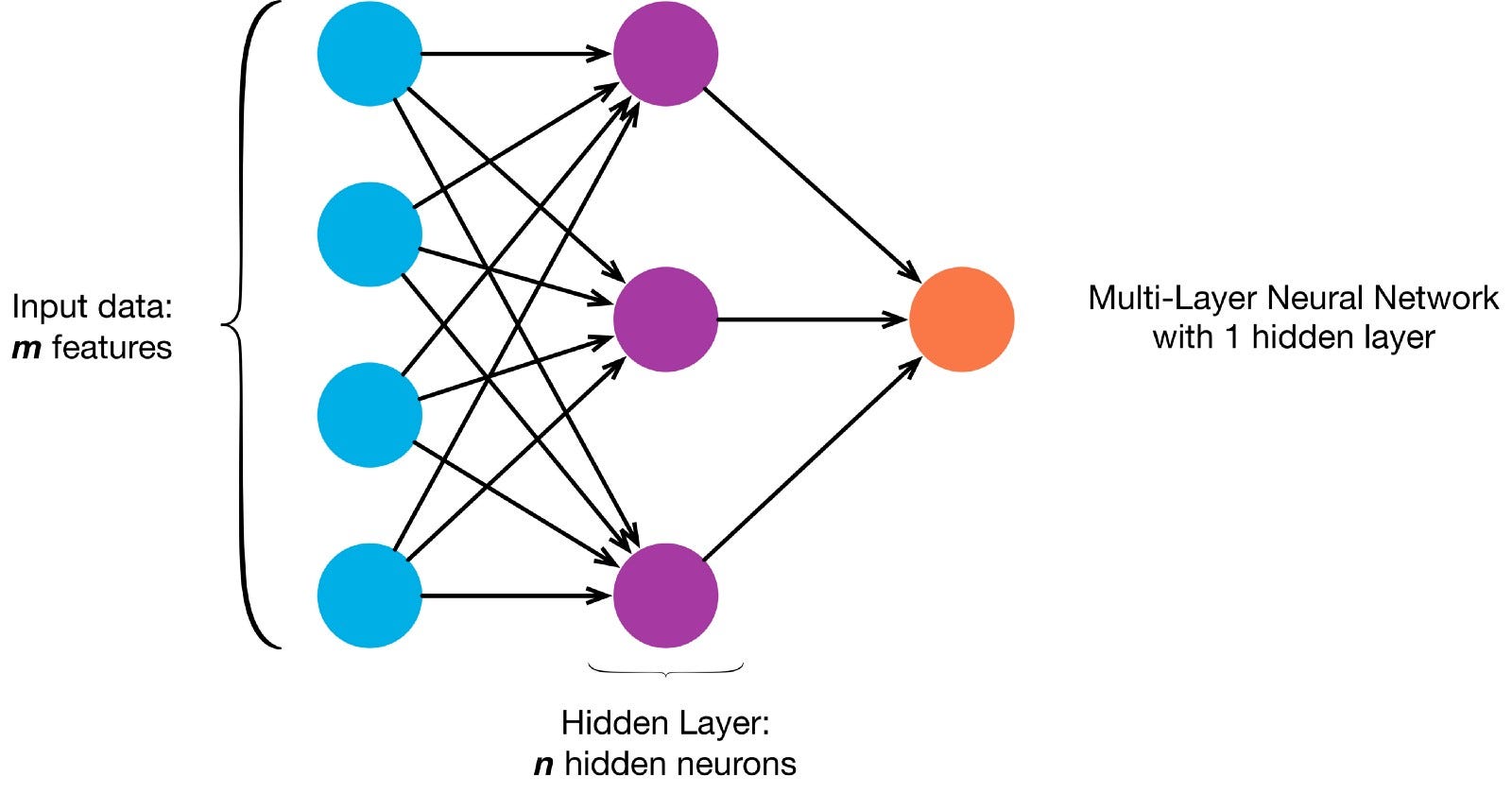
normalmente Há uma camada de entrada (contendo um número de neurônios igual ao número de recursos de entrada de dados), uma camada de saída (contendo um número de neurônios igual ao número de classes), e uma camada oculta (contendo qualquer número de neurônios).

pode haver mais de uma camada oculta para permitir que a rede neural para aprender mais complexo decisão limites (Qualquer rede neural com mais de uma camada oculta é considerado um profundo rede neural).
vamos construir um NN profundo para pintar esta imagem:

Permite fazer o download da imagem e carregar seus pixels em uma matriz
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
Agora, o ensino a ANN para pintar é um aprendizado supervisionado, de tarefas, de modo que precisamos para criar um rotulados conjunto de treinamento (Nossos dados de treinamento terá entradas e a saída esperada etiquetas para cada entrada). As entradas de treinamento terão 2 valores (as coordenadas X, y de cada pixel).
dada a simplicidade da imagem, poderíamos realmente abordar este problema de uma de duas maneiras. Um problema de classificação (onde a rede neural prevê se um pixel pertence à classe “azul” ou à classe “cinza”, dadas as suas coordenadas xy) ou um problema de regressão (onde a rede neural prevê valores RGB para um pixel dadas as suas coordenadas).
se tratar isto como um problema de regressão: as saídas de formação terão 3 valores (os valores normalizados r,g,b para cada pixel). – Vamos usar este método por agora.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
Agora vamos criar o nosso ANN:

- Ele deve ter 2 neurônios na camada de entrada (uma vez que existem 2 valores entrem em: x & y coordenadas).
- deve ter 3 neurônios na camada de saída (uma vez que existem 3 valores para aprender: r, g, b).
- O número de camadas ocultas e o número de neurônios em cada camada oculta são dois hiperparâmetros a experiência (bem como o número de épocas de treinamento para ele, a função de ativação, etc) — eu vou usar a 10 camadas ocultas com 100 neurônios em cada camada oculta (tornando este um profundo rede neural)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
A rede treinada que agora podem prever normalizado valores rgb para qualquer coordenadas (e.g. x,y = 1,1).
ann.predict(])
array(])
permite usar a ANN para prever os valores de rgb para cada coordenada e permite exibir a previsão de valores rgb da imagem inteira para ver o quão bem ele fez (qualitativamente — vamos deixar avaliação de métricas para outro tutorial)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

Tente alterar os hiperparâmetros para obter melhores resultados.
Se, em vez de tratar isso como um problema de regressão, podemos tratar isso como uma classificação problema e, em seguida, a formação de saídas de ter 2 valores (a probabilidade do pixel pertencer a cada uma das duas classes: “azul” e “cinza”)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
podemos reconstruir a nossa ANN como um classificador binário com 2 neurônios na camada de entrada, 2 neurônios na camada de saída e 100 neurônios na camada oculta (com 10 camadas ocultas)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
agora podemos usar os treinados ANN para prever a classe a qual cada pixel pertence (0: “cinza” ou 1: “azul”). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: “grey”)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

