Introdução
Análise de Componentes Principais (PCA) é uma redução de dimensionalidade algoritmo que pode ser usado para acelerar significativamente o seu supervisionada recurso algoritmo de aprendizagem. Mais importante ainda, compreender o PCA nos permitirá implementar mais tarde o clareamento, que é um passo importante de pré-processamento para muitos algoritmos.suponha que está treinando seu algoritmo em imagens. Em seguida, a entrada será um pouco redundante, porque os valores de pixels adjacentes em uma imagem são altamente correlacionados. Concretamente, suponha que estamos treinando em imagens 16×16 em tons de cinza. Então \textstyle x\in \re^{256} são vectores de 256 dimensões, com uma funcionalidade \textstyle x_ J correspondente à intensidade de cada pixel. Devido à correlação entre pixels adjacentes, o PCA nos permitirá aproximar a entrada com uma dimensional muito mais baixa, enquanto incorre em muito pouco erro.
Exemplo Matemáticas e de Fundo
Para o nosso exemplo, vamos usar um conjunto de dados \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} com \textstyle n=2 dimensional entradas, de modo que \textstyle x^{(i)} \in \Re^2. Suponha que queremos reduzir os dados de 2 dimensões para 1. (Na prática, podemos querer reduzir os dados de 256 para 50 dimensões, digamos; mas usando dados dimensionais mais baixos em nosso exemplo nos permite visualizar melhor os algoritmos.) Aqui está o nosso conjunto de dados:
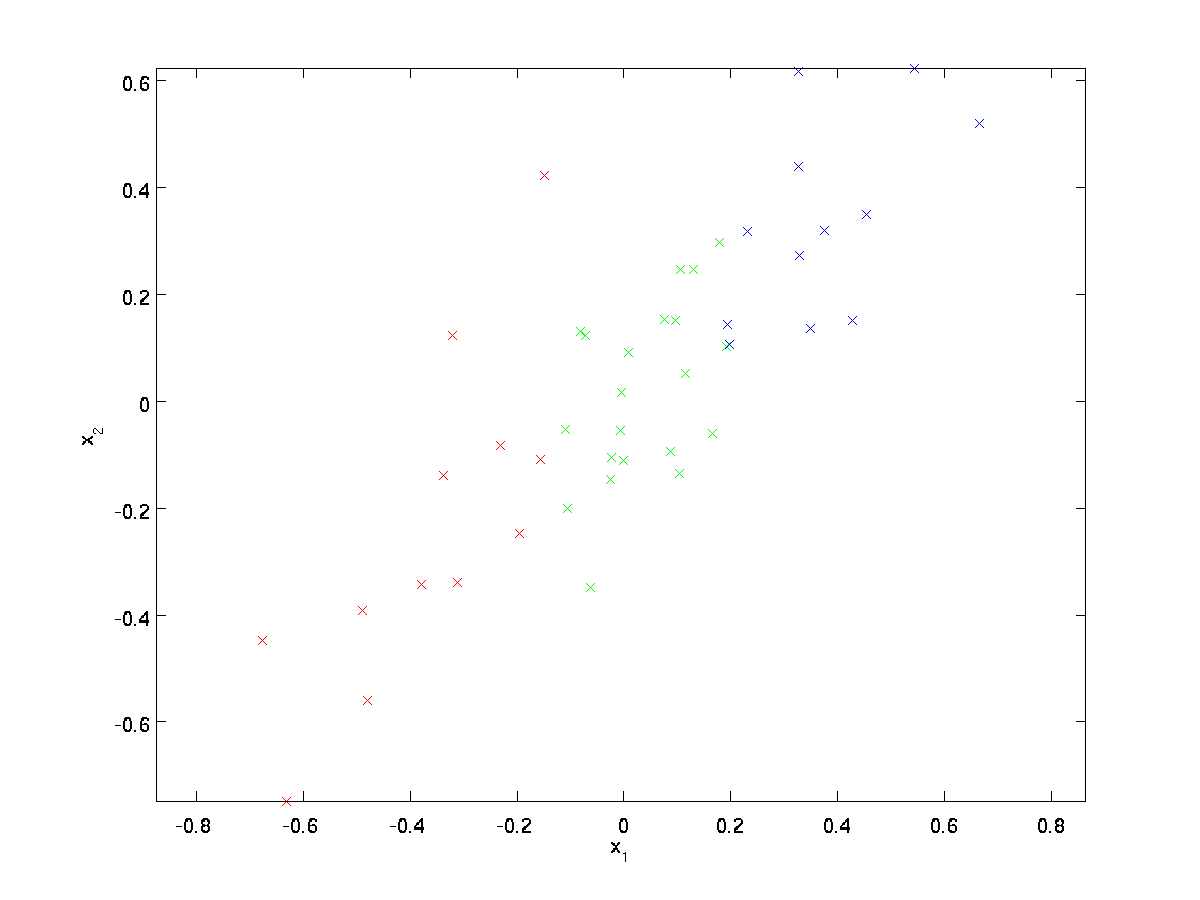
estes dados já foram pré-processados de modo que cada uma das características \textstyle x_1 e \textstyle x_2 têm aproximadamente a mesma média (zero) e variância.
para efeitos de ilustração, também colorimos cada um dos pontos uma de três cores, dependendo do seu valor \textstyle x_1; estas cores não são usadas pelo algoritmo, e são apenas para ilustração.
PCA irá encontrar um subespaço de dimensões mais baixas para projectar os nossos dados.
a Partir de examinar visualmente os dados, parece que \textstyle u_1 é o principal sentido da variação dos dados, e \textstyle u_2 a direção secundária de variação:
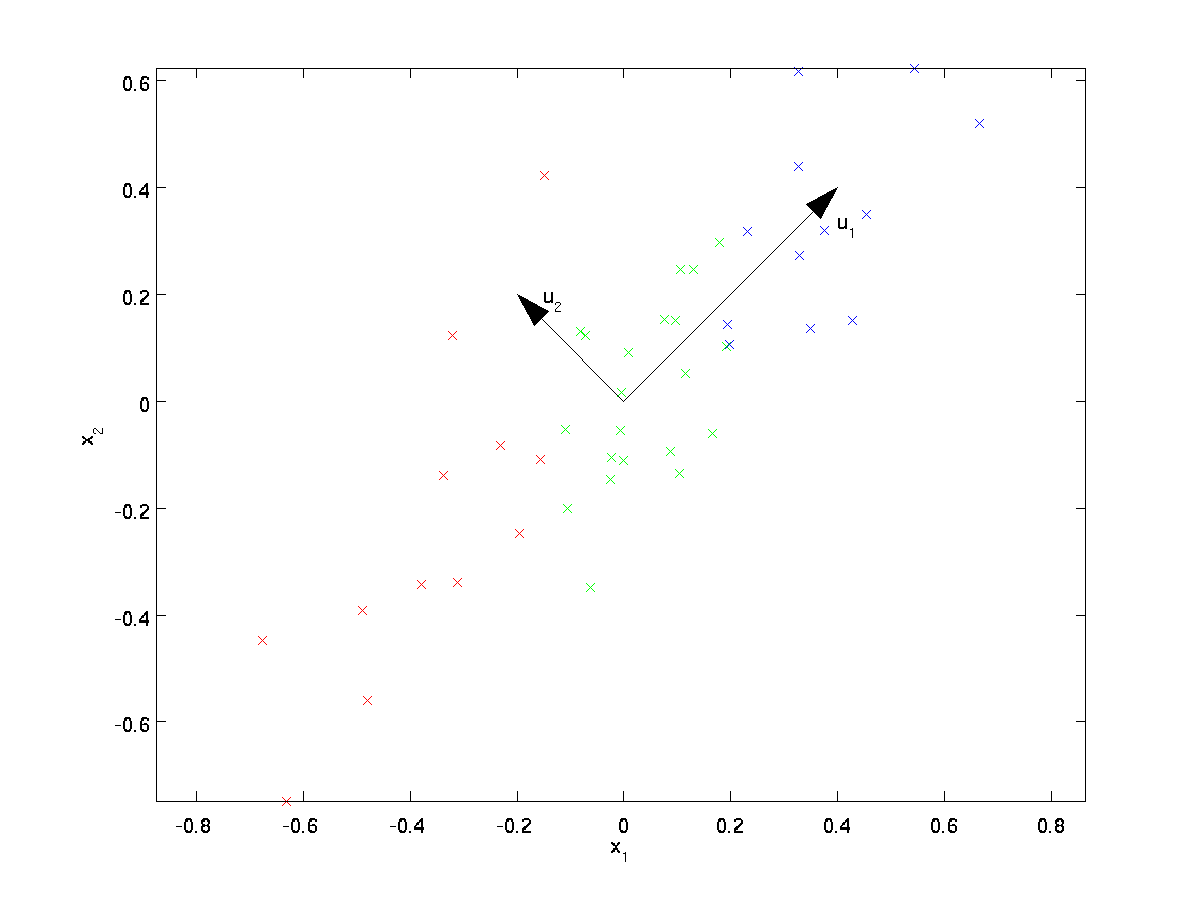
I. e., os dados variam muito mais em direção \textstyle u_1 que \textstyle u_2. Para encontrar mais formalmente as direcções \textstyle u_1 e \textstyle u_2, primeiro calculamos a matriz \textstyle \Sigma como se segue:
\begin{align}\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \end{align}
Se \textstyle x tem zero significa, em seguida, \textstyle \Sigma é exatamente a matriz de covariância de \textstyle x. (O símbolo “\textstyle \Sigma”, pronuncia-se “Sigma”, é o padrão de notação para denotar a matriz de covariância. Infelizmente, parece-se com o símbolo de soma, como em \sum_{i=1}^n i; mas estas são duas coisas diferentes.)
pode então ser mostrado que \textstyle u_1—a direcção principal da variação dos dados—é o autovetor superior (principal) de \textstyle \Sigma, e \textstyle u_2 é o segundo autovetor.
Nota: Se você está interessado em ver uma derivação matemática mais formal / justificação deste resultado, veja as notas de leitura CS229 (aprendizagem de máquinas) no PCA (link no final desta página). No entanto, não será necessário fazê-lo para seguir este curso.
Você pode usar o software padrão de álgebra linear numérica para encontrar esses autovetores (veja notas de implementação). Concretamente, vamos calcular OS autovectores de \textstyle \Sigma e empilhar os autovectores em colunas para formar a matriz \textstyle U:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.
os vectores \textstyle u_1 e \textstyle u_2 no nosso exemplo formam uma nova base na qual podemos representar os dados. Concretamente, que \textstyle x \in \RE^2 seja um exemplo de formação. Então \textstyle u_1^Tx é o comprimento (magnitude) da projeção de \textstyle x no vetor \textstyle u_1.
similarmente, \textstyle u_2^Tx é a magnitude do \textstyle x projectado no vetor \textstyle u_2.
Girar os Dados
Assim, podemos representar \textstyle x em a \textstyle (u_1, u_2)-base de computação
\begin{align}x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}
(O subscrito “rot” vem da observação de que esta corresponde a uma rotação (e, possivelmente, de reflexão) dos dados originais. Permite levar todo o conjunto de treinamento e de computação \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)} para cada \textstyle eu. Plotagem de dados transformados \textstyle x_{\rm rot}, temos:

Este é o conjunto de treino rotacionado para a base \textstyle u_1,\textstyle u_2. No caso geral, \textstyle U^Tx será o conjunto de treinamento rodado na base \textstyle u_1,\textstyle u_2, …,\textstyle u_n.
Uma das propriedades de \textstyle U é que ele é um “ortogonal” matriz, o que significa que satisfaz \textstyle U^TU = UU^T = I. Assim, se você precisar ir a partir rodado vetores \textstyle x_{\rm rot} de volta para o original data \textstyle x, você pode calcular
\begin{align}x = U x_{\rm rot} ,\end{align}
devido a \textstyle U x_{\rm rot} = UU^T x = x.
Reduzir a Dimensão de Dados
Nós vemos que a principal direcção de variação dos dados é a primeira dimensão \textstyle x_{\rm rot,1} esta rodada de dados. Assim, se queremos reduzir esses dados para uma dimensão, podemos definir
\begin{align}\til{x}^{(i)} = x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} \in \Re.\end{align}
Mais geralmente, se \textstyle x \in \Re^n e queremos reduzi-lo a um \textstyle k dimensional representação \textstyle \til{x} \in \Re^k (onde k < n), que iria dar a primeira \textstyle k componentes de \textstyle x_{\rm rot}, que corresponde ao topo \textstyle k direções de variação.
outra forma de explicar PCA é que \textstyle x_{\rm rot} é um vetor \ textstyle n dimensional, onde os primeiros componentes são provavelmente grandes (e.g. no nosso exemplo, nós vimos que \textstyle x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} leva razoavelmente grande de valores para a maioria dos exemplos \textstyle i) e, mais tarde, os componentes são susceptíveis de ser pequeno (por exemplo, no nosso exemplo, \textstyle x_{\rm rot,2}^{(i)} = u_2^Tx^{(i)} era mais provável ser pequeno). O que o PCA não cai a tarde (menor) componentes de \textstyle x_{\rm rot}, e apenas aproxima-los com 0’s. Concretamente, a nossa definição de \textstyle \til{x} também pode ser alcançada usando uma aproximação \textstyle x_{\rm rot}, onde todos, mas o primeiro \textstyle k componentes são zeros. Em outras palavras, tem-se:
\begin{align}\til{x} = \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\approx \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\x_{\rm rot,k+1} \\\vdots \\ x_{\rm rot,n} \end{bmatrix}= x_{\rm rot} \end{align}
No nosso exemplo, este dá-nos a seguinte enredo de \textstyle \til{x} (usando \textstyle n=2, k=1):

no Entanto, desde o final \textstyle n-k componentes de \textstyle \til{x} como definido acima seria sempre zero, não há nenhuma necessidade de manter estes zeros em torno, e assim definimos \textstyle \til{x} como \textstyle k-dimensional vetor com apenas a primeira \textstyle k (diferente de zero) componentes.
isto também explica porque é que queríamos expressar os nossos dados no \textstyle u_1, u_2, \ldots, base u_n: decidir quais os componentes a manter torna-se apenas manter os componentes top \textstyle K. Quando fazemos isso, também dizemos que estamos “mantendo o topo \textstyle K PCA (ou principal) componentes.”
a Recuperação de uma Aproximação dos Dados
Agora, \textstyle \til{x} \in \Re^k é uma versão de baixo-dimensional, “compactado” de representação do original \textstyle x \in \Re^n. Dado \textstyle \til{x}, como podemos recuperar uma aproximação \textstyle \hat{x} para o valor original de \textstyle x? A partir de uma secção anterior, sabemos que \textstyle x = U x_{\rm rot}. Além disso, podemos pensar no \textstyle \tilde{x} como uma aproximação ao \textstyle x_{\rm rot}, onde definimos os últimos componentes do \textstyle n-k como zeros. Assim, dada \textstyle \til{x} \in \Re^k, podemos preencher com \textstyle n-k zeros para receber a nossa aproximação \textstyle x_{\rm rot} \in \Re^n. Finalmente, nós pré-multiplicar por \textstyle U para receber a nossa aproximação \textstyle x. Concretamente, temos
\begin{align}\hat{x} = U \begin{bmatrix} \til{x}_1 \\ \vdots \\ \til{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \til{x}_i. \end{align}
a igualdade final acima vem da definição de \ textstyle U dada anteriormente. (Em uma implementação prática, não seria, de fato, zero pad \textstyle \til{x} e, em seguida, multiplique por \textstyle U, desde que significaria multiplicar um monte de coisas por zeros; em vez disso, tínhamos apenas multiplicar \textstyle \til{x} \in \Re^k com o primeiro \textstyle k colunas de \textstyle U como na final da expressão acima.) Aplicando isto ao nosso conjunto de dados, obtemos o seguinte gráfico para \textstyle \hat{x}:
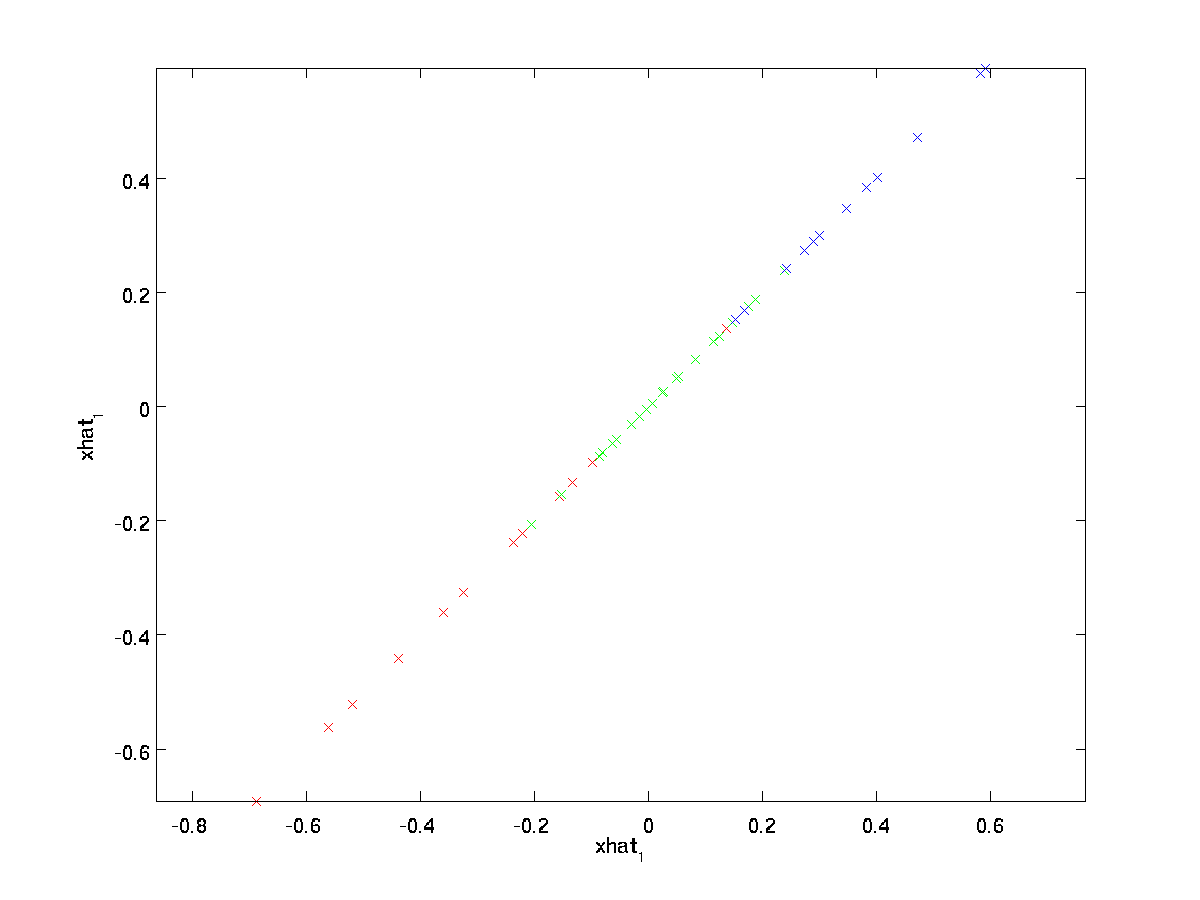
estamos, portanto, a utilizar uma aproximação 1 dimensional ao conjunto de dados original.
Se estiver a treinar um auto-codificador ou outro algoritmo de aprendizagem de funcionalidades não supervisionado, o tempo de execução do seu algoritmo irá depender da dimensão da entrada. Se alimentar o \textstyle \tilde{x} \in \re^k no seu algoritmo de aprendizagem em vez de \textstyle x, então estará a treinar com uma entrada de dimensões mais baixas, pelo que o seu algoritmo poderá correr significativamente mais depressa. Para muitos conjuntos de dados, a representação lower dimensional \textstyle \tilde{x} pode ser uma aproximação extremamente boa para o original, e usando o PCA desta forma pode acelerar significativamente o seu algoritmo Ao introduzir muito pouco erro de aproximação.
número de componentes para reter
como definir \textstyle k; ou seja, quantos componentes PCA devemos reter? No nosso exemplo bidimensional simples, parecia natural reter 1 dos 2 componentes, mas para dados dimensionais mais elevados, esta decisão é menos trivial. Se o \textstyle k for demasiado grande, então não estaremos a comprimir muito os dados; no limite de \textstyle k=n, então estamos apenas a usar os dados originais (mas rodados numa base diferente). Inversamente, se \textstyle k é muito pequeno, então nós podemos estar usando uma aproximação muito ruim para os dados.
Para decidir como definir \textstyle k, nós geralmente a olhar para o “percentual de variância retida”‘ para diferentes valores de \textstyle k. Concretamente, se \textstyle k=n, então temos uma exata aproximação para os dados, e podemos dizer que 100% da variância é mantida. Seja., toda a variação dos dados originais é mantida. Inversamente, se \textstyle k=0, então estamos aproximando todos os dados com o vetor zero, e assim 0% da variância é retida.
Mais geralmente, deixe \textstyle \lambda_1, \lambda_2, \ldots, \lambda_n ser os autovalores de \textstyle \Sigma (classificados em ordem decrescente), de modo que \textstyle \lambda_j é o eigenvalue correspondente para o eigenvector \textstyle u_j. Em seguida, se mantivermos \textstyle k componentes principais, a percentagem de variância retida é dada por:
\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j}.\end{align}
no nosso exemplo 2D simples acima, \textstyle \lambda_1 = 7.29, e \textstyle \lambda_2 = 0.69. Assim, mantendo apenas \textstyle K=1 Componentes principais, mantivemos \textstyle 7.29/(7.29+0.69) = 0.913, ou 91,3% da variância.
uma definição mais formal de porcentagem de variância retida está além do escopo destas notas. No entanto, é possível mostrar que \textstyle \lambda_j =\sum_{i=1}^m x_{\rm rot, j}^2. Assim, se \textstyle \lambda_j \ approx 0, que mostra que \textstyle x_{\rm rot, j} é geralmente próximo de 0 de qualquer forma, e nós perdemos relativamente pouco ao aproximá-lo com uma constante 0. Isto também explica por que mantemos os componentes principais de topo (correspondendo aos valores maiores de \textstyle \lambda_j) em vez dos de baixo. Os componentes principais de topo \textstyle x_{\rm rot,j} são os que são mais variáveis e que assumem valores maiores, e para os quais teríamos um erro de aproximação maior se os ajustássemos a zero.
no caso das imagens, uma heurística comum é escolher \textstyle k de modo a manter 99% da variância. Por outras palavras, escolhemos o menor valor de \textstyle k que satisfaz
\ begin{align}\frac {\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0.99. \end{align}
dependendo da aplicação, se você estiver disposto a incorrer em algum erro adicional, os valores no intervalo de 90-98% também são usados às vezes. Quando você descreve aos outros como você aplicou o PCA, dizendo que você escolheu o \ textstyle k para reter 95% da variância também será uma descrição muito mais facilmente interpretável do que dizer que você reteve 120 (ou qualquer outro número de) componentes.
PCA nas imagens
para o PCA funcionar, normalmente queremos que cada uma das características \textstyle x_1, x_2, \ldots, x_n tenha uma gama de valores semelhante aos outros (e ter uma média próxima de zero). Se você já usou o PCA em outras aplicações antes, você pode, portanto, ter pré-processado separadamente cada recurso para ter a média zero e variância de unidade, estimando separadamente a média e variância de cada característica \textstyle x_ J. No entanto, este não é o pré-processamento que vamos aplicar à maioria dos tipos de imagens. Especificamente, suponha que estamos treinando nosso algoritmo em “‘imagens naturais”‘, de modo que \textstyle x_j é o valor de pixel \textstyle J. por “imagens naturais”, informalmente significamos o tipo de imagem que um animal típico ou pessoa pode ver ao longo de sua vida.Nota: Normalmente usamos imagens de cenas ao ar livre com grama, árvores, etc., e cortar pequenos (digamos 16×16) patches de imagem aleatoriamente a partir destes para treinar o algoritmo. Mas na prática, a maioria dos algoritmos de aprendizagem de recursos são extremamente robustos para o tipo exato de imagem em que é treinado, então a maioria das imagens tomadas com uma câmera normal, desde que eles não sejam excessivamente desfocados ou tenham artefatos estranhos, deve funcionar.
ao treinar em imagens naturais, faz pouco sentido estimar uma média e variância separadas para cada pixel, porque as estatísticas em uma parte da imagem devem (teoricamente) ser as mesmas que qualquer outra.esta propriedade de imagens é chamada de “‘ stationarity.”‘
in detail, in order for PCA to work well, informally we require that (i) The features have approximately zero mean, and (ii) The different features have similar variances to each other. Com imagens naturais, (ii) já está satisfeito, mesmo sem a normalização da variância, e por isso não vamos realizar qualquer normalização da variância.
(Se você está treinando em dados de áudio-say, em espectrogramas—ou em dados de texto—say, bag-of-word vetores—normalmente não realizaremos a normalização da variância também.)
Na verdade, PCA é invariante à escala dos dados, e irá retornar os mesmos autovetores independentemente da escala da entrada. Mais formalmente, se você multiplicar cada recurso vector \textstyle x por algum número positivo (assim, dimensionando cada recurso em cada exemplo de treino pelo mesmo número), os autovectores de saída do PCA não irão mudar.
assim, não usaremos a normalização da variância. A única normalização que precisamos realizar então é a normalização média, para garantir que as características têm uma média em torno de zero. Dependendo da aplicação, muitas vezes não estamos interessados em quão brilhante é a imagem de entrada global. Por exemplo, nas tarefas de reconhecimento de objetos, o brilho total da imagem não afeta os objetos que existem na imagem. Mais formalmente, não estamos interessados no valor de intensidade média de um patch de imagem; assim, podemos subtrair este valor, como uma forma de normalização média.
Concretamente, se \textstyle x^{(i)} \in \Re^{n} são os (escala de cinza) de valores de intensidade de uma imagem de 16 x 16 patch (\textstyle n=256), podemos normalizar a intensidade de cada imagem \textstyle x^{(i)} da seguinte forma:
\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_jx^{(i)}_j := x^{(i)}_j – \mu^{(i)}
para todos \textstyle j
Observe que as duas etapas acima são feitas em separado para cada imagem \textstyle x^{(i)}, e que \textstyle \mu^{(i)} aqui é a intensidade média da imagem \textstyle x^{(i)}. Em particular, esta não é a mesma coisa que estimar um valor médio separadamente para cada pixel \textstyle x_j.
Se você está treinando seu algoritmo em imagens que não imagens naturais (por exemplo, imagens de caracteres manuscritos, ou imagens de objetos isolados centrados em um fundo branco), outros tipos de normalização podem valer a pena considerar, e a melhor escolha pode ser dependente da aplicação. Mas quando o treinamento em imagens naturais, usando o método de normalização média por imagem como dado nas equações acima seria um padrão razoável.
Clareamento
usamos PCA para reduzir a dimensão dos dados. Há um passo de pré-processamento intimamente relacionado chamado clareamento (ou, em algumas outras literaturas, esfrega) que é necessário para alguns algoritmos. Se estamos treinando em imagens, a entrada em bruto é redundante, uma vez que os valores de pixels adjacentes estão altamente correlacionados. O objetivo do clareamento é tornar a entrada menos redundante; mais formalmente, nosso desiderata é que nossos algoritmos de aprendizagem vê uma entrada de treinamento onde (i) as características são menos correlacionadas umas com as outras, e (ii) as características todas têm a mesma variância.
2D exemplo
vamos primeiro descrever o clareamento usando o nosso exemplo anterior de 2D. Vamos então descrever como isso pode ser combinado com suavização, e finalmente como combinar isso com PCA.
Como podemos fazer nossas características de entrada não correlacionadas umas com as outras? Já tínhamos feito isto ao computar \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}.
Repetir nossos figura anterior, o nosso enredo de \textstyle x_{\rm rot} foi:

A matriz de covariância dos dados é dada por:
\begin{align}\begin{bmatrix}7.29 && 0.69\end{bmatrix}.\end{align}
(Nota: Tecnicamente, muitas das afirmações nesta seção sobre a” covariância ” só serão verdadeiras se os dados tiverem média zero. No resto desta seção, tomaremos esta suposição como implícita em nossas declarações. No entanto, mesmo que a média dos dados não seja exatamente zero, as intuições que apresentamos aqui ainda são verdadeiras, e então isso não é algo com o qual você deve se preocupar.)
não é por acaso que os valores diagonais são \textstyle \lambda_1 e \textstyle \lambda_2. Além disso, as entradas fora-diagonais são zero; assim, \textstyle x_{\rm rot, 1} e \textstyle x_{\rm rot, 2} não estão correlacionados, satisfazendo um dos nossos desiderata para dados brancos (que as características sejam menos correlacionadas).
para fazer com que cada uma das nossas funcionalidades de entrada tenha variância de unidade, podemos simplesmente rever cada funcionalidade \textstyle x_{\rm rot, i} por \textstyle 1/\sqrt{\lambda_i}. Concretamente, definimos os nossos dados brancos \textstyle x_{\rm PCAwhite} \in \Re^n do seguinte modo:
\begin{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} {\sqrt{\lambda_i}}. \end{align}
Plotting \textstyle x_{\rm PCAwhite}, nós obtemos:

esses dados agora tem covariância igual a matriz identidade \textstyle I. dizemos que \textstyle x_{\rm PCAwhite} é o nosso PCA branqueada de versão dos dados: Os diferentes componentes do \textstyle x_{\rm PCAwhite} eles nada têm a ver e ter a unidade de variância.
Clareamento combinado com redução de dimensionalidade. Se quiser ter dados que sejam brancos e que sejam de dimensão inferior à entrada original, também poderá, opcionalmente, manter apenas os componentes top \textstyle k do \textstyle x_{\rm PCAwhite}. Quando combinamos o clareamento do PCA com a regularização (descrita mais tarde), os últimos componentes do \textstyle x_{\rm PCAwhite} serão quase nulos de qualquer forma, e assim podem ser descartados com segurança.
ZCA clarificando
finalmente, acontece que esta maneira de obter os dados para ter identidade covariância \textstyle I não é único. Concretamente, se \textstyle R é qualquer matriz ortogonal, de modo que ela satisfaça \textstyle RR^T = R^TR = I (menos formalmente, se \textstyle R é uma rotação, reflexão matriz), em seguida, \textstyle R \,x_{\rm PCAwhite} também terá de identidade covariância.
Na ZCA clareamento, escolhemos \textstyle R = U. definimos
\begin{align}x_{\rm ZCAwhite} = U x_{\rm PCAwhite}\end{align}
Plotagem \textstyle x_{\rm ZCAwhite}, temos:

por Isso, pode ser mostrado que, de todas as opções possíveis para \textstyle R, essa opção de rotação faz com que \textstyle x_{\rm ZCAwhite} para ser o mais próximo possível do original de entrada de dados \textstyle x.
Ao usar ZCA clareamento (ao contrário da PCA clareamento), nós, geralmente, manter todos os \textstyle n dimensões dos dados, e não tente reduzir a sua dimensão.
Regularizaton
Quando a implementação do PCA clareamento ou ZCA clareamento na prática, às vezes, alguns dos autovalores \textstyle \lambda_i será numericamente próximo a 0, e, portanto, a escala etapa onde dividimos por \sqrt{\lambda_i} envolveria a divisão por um valor próximo de zero; isto pode causar a dados para explodir (grandes valores) ou de outra forma ser numericamente instável. Na prática, nós, portanto, implementar esta escala passo, usando uma pequena quantidade de regularização, e adicionar uma pequena constante \textstyle \epsilon para os autovalores antes de tomar a sua raiz quadrada e inverso:
\begin{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i + \epsilon}}.\end{align}
Quando o \textstyle x toma valores em torno do \textstyle, um valor de \textstyle \epsilon \approx 10^{-5} pode ser típico.
para o caso das imagens, a adição do \textstyle \epsilon aqui também tem o efeito de suavizar ligeiramente (ou filtragem de baixa passagem) a imagem de entrada. Isso também tem um efeito desejável de remover artefatos aliasing causados pela forma como pixels são dispostos em uma imagem, e pode melhorar as características aprendidas (detalhes estão além do escopo dessas notas).
ZCA whitening é uma forma de pré-processamento dos dados que o mapeia de \textstyle x para \textstyle x_{\rm ZCAwhite}. Acontece que este também é um modelo áspero de como o olho biológico (a retina) processa imagens. Especificamente, como seu olho percebe imagens, a maioria dos “pixels” adjacentes em seu olho vai perceber valores muito semelhantes, uma vez que partes adjacentes de uma imagem tendem a ser altamente correlacionados em intensidade. É, portanto, um desperdício para o seu olho ter de transmitir cada pixel separadamente (através do seu nervo óptico) para o seu cérebro. Em vez disso, sua retina realiza uma operação de decorrelação (isto é feito através de neurônios retinais que computam uma função chamada “no centro, off surround/off Centro, On surround”), que é semelhante à realizada pela ZCA. Isto resulta em uma representação menos redundante da imagem de entrada, que é então transmitida ao seu cérebro.
Implementing PCA Whitening
nesta secção, resumimos os algoritmos PCA, PCA whitening e ZCA whitening, e também descrevemos como você pode implementá-los usando bibliotecas de álgebra linear eficientes.
primeiro, precisamos garantir que os dados têm (aproximadamente) média zero. Para imagens naturais, conseguimos isso (aproximadamente) subtraindo o valor médio de cada patch de imagem.
conseguimos isto computando a média para cada patch e subtraindo-a para cada patch. No Matlab, podemos fazer isso usando
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);em seguida, precisamos de computação \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. Se você estiver implementando esta em Matlab (ou mesmo se você está a implementar isso em C++, Java, etc., mas ter acesso a uma eficiente biblioteca de álgebra linear), fazê-lo como uma soma explícita é ineficiente. Em vez disso, podemos computar isso de uma só vez como
sigma = x * x' / size(x, 2);(Verifique a matemática por si mesmo para ver a correção.) Aqui, assumimos que x é uma estrutura de dados que contém um exemplo de treinamento por coluna (então, x é um \textstyle n-by-\textstyle m matrix).
A seguir, PCA calcula os autovectores de \Sigma. Pode – se fazer isso usando a função EIG Matlab. No entanto, porque \ Sigma é uma matriz semi-definitiva positiva simétrica, é mais confiável numericamente para fazer isso usando a função svd. Concretamente, se você implementar
= svd(sigma);em seguida, a matriz U irá conter os autovetores de \Sigma (um eigenvector por coluna, classificados em ordem de cima para baixo eigenvector), e as entradas da diagonal da matriz S conterá os correspondentes autovalores (também classificados em ordem decrescente). A matriz V será igual a U, e pode ser ignorada com segurança.
(Nota:: A função svd realmente calcula os vetores singulares e os valores singulares de uma matriz, que para o caso especial de uma matriz semi-definida positiva simétrica—que é tudo o que estamos preocupados aqui—é igual a seus autovetores e autovalores. Uma discussão completa de vetores singulares vs. autovetores está além do escopo dessas notas.)
Finalmente, você pode calcular \textstyle x_{\rm rot} e \textstyle \til{x} da seguinte forma:
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keepIsso dá a sua PCA representação dos dados em termos de \textstyle \til{x} \in \Re^k. Incidentalmente, se x é uma matriz n-by-\textstyle m com todos os seus dados de treino, esta é uma implementação vectorizada, e as expressões acima funcionam também para computar x_ {\rm rot} e\tilde{x} para todo o seu conjunto de treino de uma só vez. O x_{\rm rot} e \tilde{x} resultante terão uma coluna correspondente a cada exemplo de treino.
Para calcular o PCA branqueada de dados \textstyle x_{\rm PCAwhite}, use
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;Desde que S diagonal contém os autovalores \textstyle \lambda_i, isto acaba por ser uma maneira compacta de computação \textstyle x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}} simultaneamente para todos \textstyle eu.
Finalmente, você também pode calcular a ZCA branqueada de dados \textstyle x_{\rm ZCAwhite} como:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;