Qu’est-ce qu’un modèle ARIMAX ?

Quel est le modèle ARIMAX ?

Si vous avez lu notre série de tutoriels de blog sur les modèles d’estimation de données de séries chronologiques, vous connaissez déjà 3 approches principales : l’autorégression, les moyennes mobiles et l’intégration.

Quel est le thème commun à tous ces modèles ?

Ils reposaient uniquement sur une seule variable.

Cependant, un modèle peut également prendre en compte plus que les prix passés ou les résidus passés.

Et ce sont les modèles dits « MAX », l’ARMAX étant la version non intégrée et l’ARIMAX – son équivalent intégré.

Donc, dans ce tutoriel, nous allons explorer à quoi ils ressemblent et vous montrer comment les implémenter en Python étape par étape.

Commençons, d’accord ?

Pourquoi ARMAX et ARIMAX Sont-ils appelés Modèles « MAX »?

Les noms ARMAX et ARIMAX sont respectivement des extensions de l’ARMA et de l’ARIMA. Le X ajouté à la fin signifie « exogène ». En d’autres termes, il suggère d’ajouter une variable externe distincte pour aider à mesurer notre variable endogène.

L’équation du modèle ARMAX et ARIMAX:

Comme la seule différence entre l’ARMAX et l’ARIMAX est que l’un est intégré et que l’autre ne l’est pas, nous pouvons examiner l’un d’eux et ensuite mettre en évidence la différence entre l’autre.

Nous avons exploré un modèle intégré dans notre dernier article de blog (ARIMA), alors voyons à quoi ressemble l’équation de l’ARIMAX.

ΔPt = c + ßX +ϕ1 ΔPt-1 + θ1tt-1 +tt

Bien sûr, l’équation pour l’ARMAX serait la même, sauf que nous utiliserions la variable réelle, disons P, au lieu de son delta.

Pt= c + ßX +ϕ1 Pt-1 + θ1tt-1 +tt

Décomposer l’équation d’ARIMAX :

On peut considérer l’ARMAX comme un cas particulier de l’ARIMAX, où l’ordre d’intégration est 0.

Donc, pour le reste du tutoriel, nous allons nous concentrer sur l’ARIMAX.

Et nous commencerons par décomposer les différentes parties qu’il contient. Pour commencer, Pt et Pt-1 représentent les valeurs de la période en cours et d’il y a 1 période respectivement.

De même, ϵt et ϵt-1 sont les termes d’erreur pour les deux mêmes périodes. Et, bien sûr, c n’est qu’un facteur constant de base.

Les deux paramètres, ϕ1 et θ1, expriment quelles parties de la valeur Pt-1 et de l’erreur ϵt-1 de la dernière période sont pertinentes pour estimer la période actuelle.

Maintenant, les deux nouveaux ajouts au modèle sont « X » et son coefficient β. Tout comme β, β est un coefficient qui sera estimé en fonction de la sélection du modèle et des données. Mais qu’en est-il de X ?

Qu’est-ce qu’une variable exogène ?

Eh bien, X est la variable exogène et cela peut être n’importe quelle variable qui nous intéresse.

Il peut s’agir d’une mesure variant dans le temps comme le taux d’inflation ou le prix d’un indice différent. Ou une variable catégorielle séparant les différents jours de la semaine. Il peut également s’agir d’une comptabilité booléenne pour les périodes de fête spéciales. Enfin, il peut représenter une combinaison de plusieurs facteurs externes différents.

L’idée est que ce peut être n’importe quelle ou d’autres variables qui peuvent affecter les prix, tant que nous avons les données disponibles.

De tels facteurs extérieurs sont connus sous le nom de variables exogènes dans notre régression. Nous utilisons leurs valeurs pour prédire et expliquer celle qui nous intéresse, qui se trouve être les prix actuels dans notre cas.

Comment implémenter des modèles ARMAX et ARIMAX en Python ?

Assez pratique, le paquet statsmodels est livré avec une méthode appelée ARIMA qui est entièrement capable de gérer de telles entrées supplémentaires.

Nous commençons par spécifier les caractéristiques du modèle et les ordres du modèle:

Après avoir fait cela, nous devons également spécifier l’argument exogène appelé « exog ».

La valeur que nous voulons transmettre doit être un tableau quelconque car nous souhaitons avoir des valeurs associées à chaque période de temps.

Par exemple, nous pouvons utiliser les prix S&P comme variable exogène, puisque nous les avons déjà dans nos données.

Maintenant, nous sommes prêts à adapter un modèle ARIMAX (1,1,1).

Assurez-vous de nommer votre variable de modèle de manière à la distinguer des modèles similaires. Dans ce cas, nous choisissons de le faire en ajoutant « X, spx » à la fin pour indiquer que la variable exogène est la S & P.

Ensuite, comme on peut le voir sur les extraits, nous la définissons égale à la méthode ARIMA comme précédemment, nous ajoutons la série temporelle et l’ordre, comme nous en avons l’habitude. Enfin, entre les deux, nous définissons l’argument « exog » égal à « DF SPX », ce qui indique les prix S &P.

Si nous ajustons ce modèle et imprimons son tableau récapitulatif, nous allons voir que nous obtenons une ligne supplémentaire pour les prix S&P.

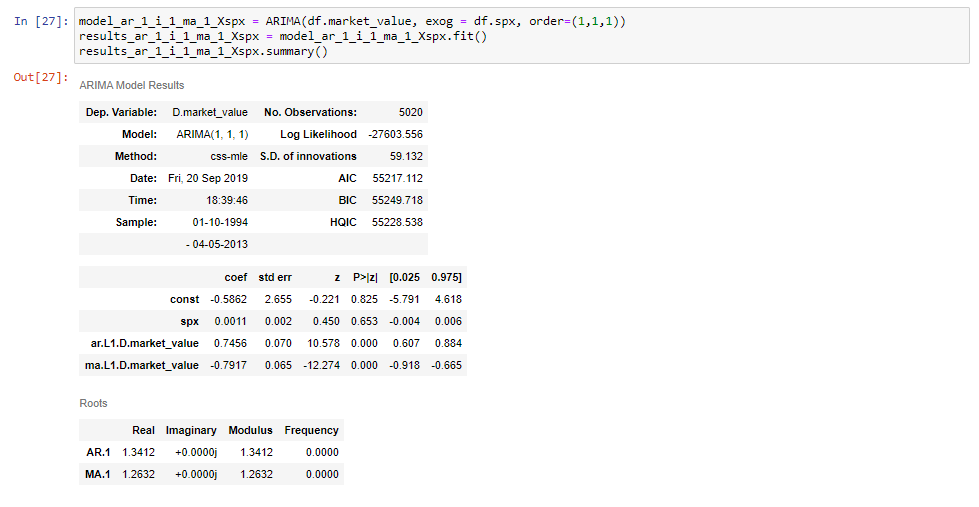
Et c’est tout ce qu’il y a à faire!

Nous avons vu avec succès comment implémenter un modèle ARIMAX en Python.

Si vous souhaitez en savoir plus sur ARIMAX et d’autres modèles de séries chronologiques en Python, assurez-vous de consulter nos tutoriels Python étape par étape. Si vous débutez en Python et que vous êtes enthousiaste à l’idée d’en apprendre davantage, cet article complet sur l’apprentissage de la programmation Python vous guidera tout au long de l’installation, en passant par lesEs, les bibliothèques et les frameworks Python, jusqu’aux meilleurs parcours de carrière et perspectives d’emploi Python.

Prêt à franchir une nouvelle étape vers une carrière en science des données ?

Découvrez le programme complet de science des données aujourd’hui. Commencez par les fondamentaux avec nos cours de statistiques, de mathématiques et Excel. Développez une expérience étape par étape avec SQL, Python, R, Power BI et Tableau. Et améliorez vos compétences avec l’Apprentissage Automatique, l’Apprentissage en Profondeur, la Modélisation du Risque de Crédit, l’Analyse de Séries chronologiques et l’Analyse des clients en Python. Vous n’êtes toujours pas sûr de vouloir transformer votre intérêt pour la science des données en carrière ? Vous pouvez explorer le programme ou vous inscrire gratuitement à 15 heures de contenu vidéo débutant à avancé en cliquant sur le bouton ci-dessous.