Înțelegerea rețelelor reziduale profunde

rețelele reziduale profunde (ResNet) au luat cu asalt lumea învățării profunde atunci când Microsoft Research a lansat învățarea reziduală profundă pentru recunoașterea imaginilor. Aceste rețele au dus la intrări câștigătoare pe locul 1 în toate cele cinci piese principale ale concursurilor ImageNet și COCO 2015, care au acoperit clasificarea imaginilor, detectarea obiectelor și segmentarea semantică. Robustețea Resnet-urilor a fost dovedită de atunci prin diferite sarcini de recunoaștere vizuală și prin sarcini non-vizuale care implică vorbire și limbaj. De asemenea, am folosit ResNet pe lângă alte modele de învățare profundă în cercetarea disertației mele de doctorat.

această postare va rezuma cele trei lucrări de mai jos, care sunt toate scrise sau co-scrise de inventatorul Resnet Kaiming He, deoarece cred că lucrările originale oferă cea mai intuitivă și detaliată explicație a modelului / rețelelor. Sperăm că această postare vă poate ajuta să înțelegeți mai bine esența rețelelor reziduale.

• învățare reziduală profundă pentru recunoașterea imaginilor
• mapări de identitate în rețele reziduale profunde
• transformare reziduală agregată pentru rețele neuronale profunde

intuiție pe rețeaua reziduală profundă (stackoverflow ref)

un bloc rezidual este afișat după cum urmează:

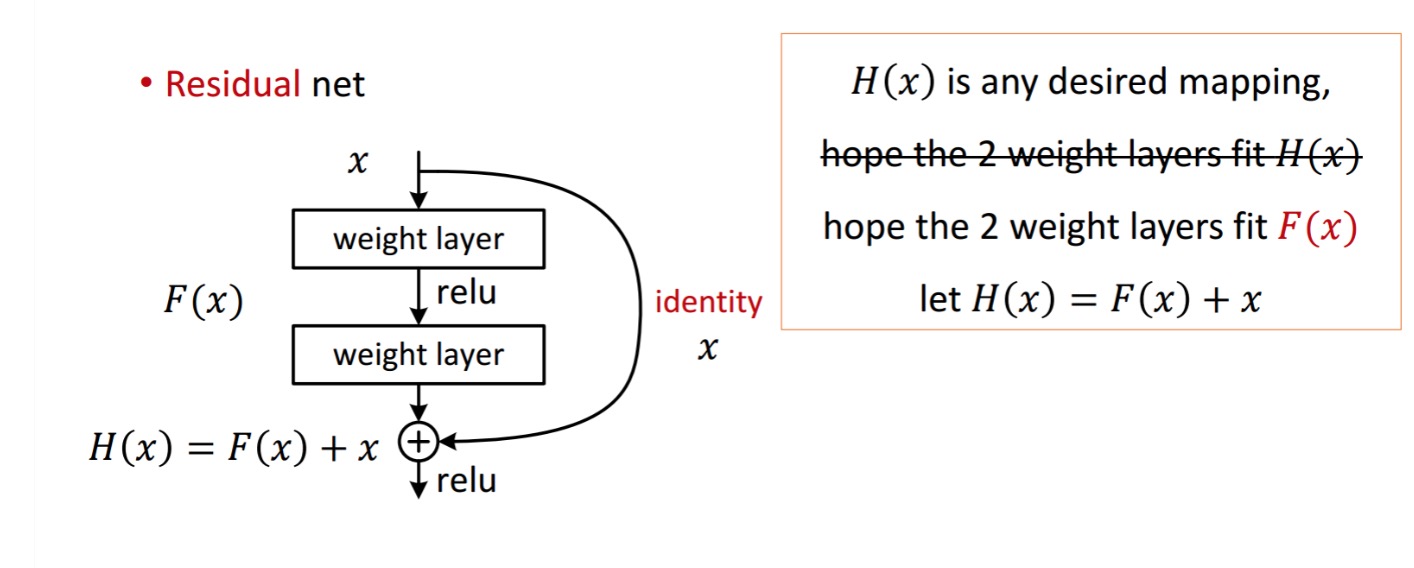
deci, unitatea reziduală prezentată obține prin prelucrarea cu două straturi de greutate. Apoi se adaugă pentru a obține . Acum, să presupunem că este rezultatul ideal prezis care se potrivește cu adevărul vostru de la sol. Deoarece, obținerea doritului depinde de obținerea perfectă . Asta înseamnă că cele două straturi de greutate din unitatea reziduală ar trebui să poată produce ceea ce doriți , apoi obținerea idealului este garantată.

se obține după cum urmează.

se obține după cum urmează.

autorii presupun că cartografierea reziduală (adică ) poate fi mai ușor de optimizat decât . Pentru a ilustra cu un exemplu simplu, presupunem că idealul . Apoi, pentru o cartografiere directă ar fi dificil să înveți o cartografiere a identității, deoarece există un teanc de straturi neliniare după cum urmează.deci, pentru a aproxima cartografierea identității cu toate aceste greutăți și ReLUs în mijloc ar fi dificil.

acum, dacă definim maparea dorită , atunci avem nevoie doar obține după cum urmează.

realizarea celor de mai sus este ușoară. Doar setați orice greutate la zero și veți obține o ieșire zero. Adăugați înapoi și veți obține cartografierea dorită.

învățare reziduală profundă pentru recunoașterea imaginilor

problemă

când rețelele mai profunde încep să convergă, a fost expusă o problemă de degradare: odată cu creșterea adâncimii rețelei, precizia se saturează și apoi se degradează rapid.

văzând degradarea în acțiune:

Să luăm o rețea superficială și omologul său mai profund adăugând mai multe straturi la ea.

scenariul cel mai rău caz: straturile timpurii ale modelului Deeper pot fi înlocuite cu rețea superficială, iar straturile rămase pot acționa doar ca o funcție de identitate (intrare egală cu ieșire).

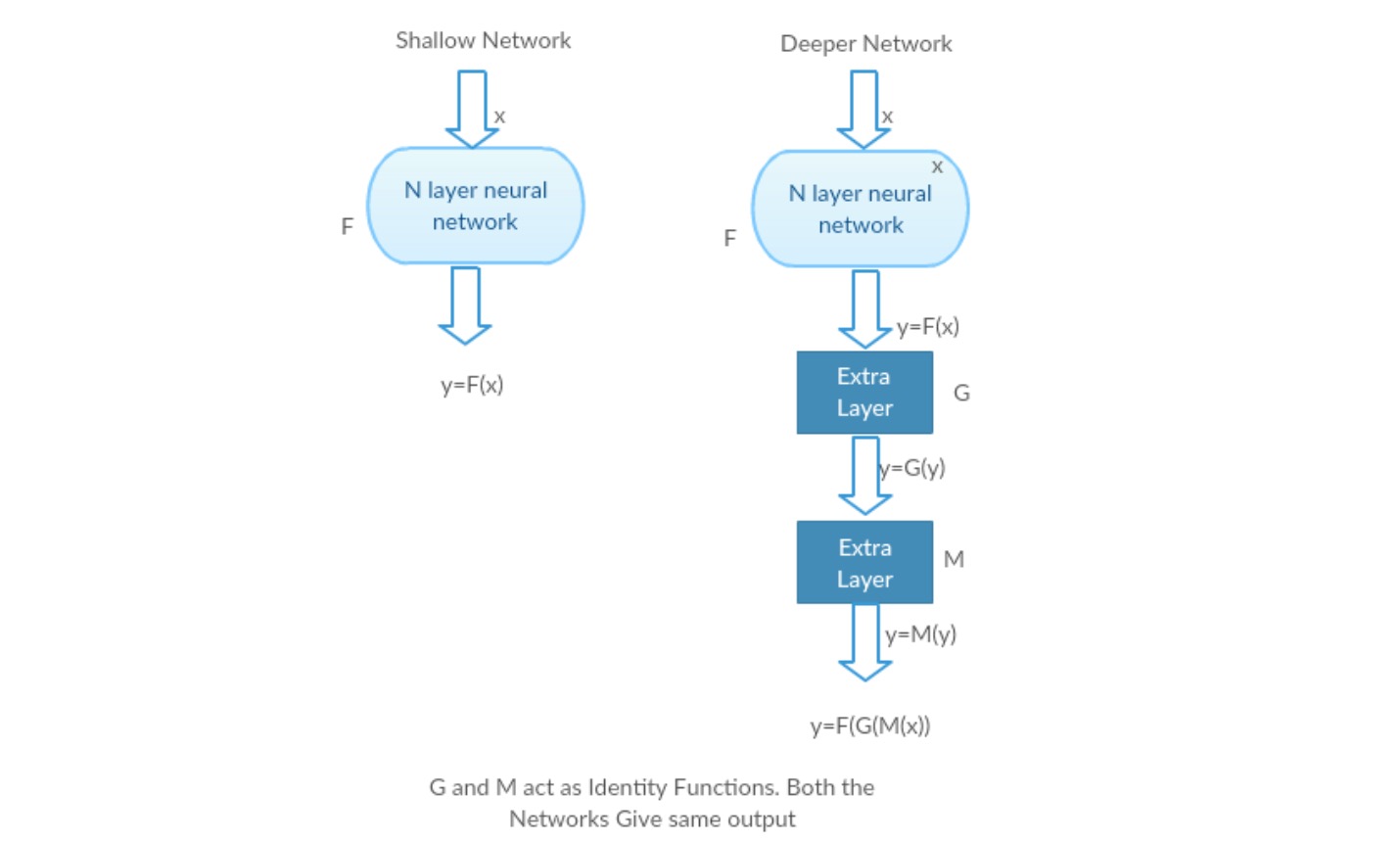
scenariu de recompensare: în rețeaua mai profundă straturile suplimentare aproximează mai bine maparea decât partea contorului mai puțin adânc și reduc eroarea cu o marjă semnificativă.

Experiment: În cel mai rău caz, atât rețeaua superficială, cât și varianta mai profundă a acesteia ar trebui să ofere aceeași precizie. În cazul scenariului de recompensare, modelul mai profund ar trebui să ofere o precizie mai bună decât partea inferioară a contorului. Dar experimentele cu rezolvatorii noștri prezenți arată că modelele mai profunde nu funcționează bine. Deci, utilizarea rețelelor mai profunde degradează performanța modelului. Aceste lucrări încearcă să rezolve această problemă folosind Cadrul de învățare reziduală profundă.

cum de a rezolva?

în loc de a învăța o mapare directă a cu o funcție (câteva straturi neliniare stivuite). Să definim funcția reziduală folosind , care poate fi reformulat în, unde și reprezintă straturile neliniare stivuite și funcția de identitate(intrare=ieșire) respectiv.

ipoteza autorului este că este ușor să optimizați funcția de mapare reziduală decât să optimizați maparea originală, fără referință .

intuiția din spatele blocurilor reziduale:

să luăm ca exemplu cartografierea identității (de exemplu ). Dacă maparea identității este optimă, putem împinge cu ușurință reziduurile la zero () decât să potrivim o mapare a identității () printr-un teanc de straturi neliniare. În limbaj simplu, este foarte ușor de a veni cu o soluție ca, mai degrabă decât folosind stiva de straturi non-lineare cnn ca funcție (gândiți-vă la asta). Deci, această funcție este ceea ce autorii au numit funcția reziduală.

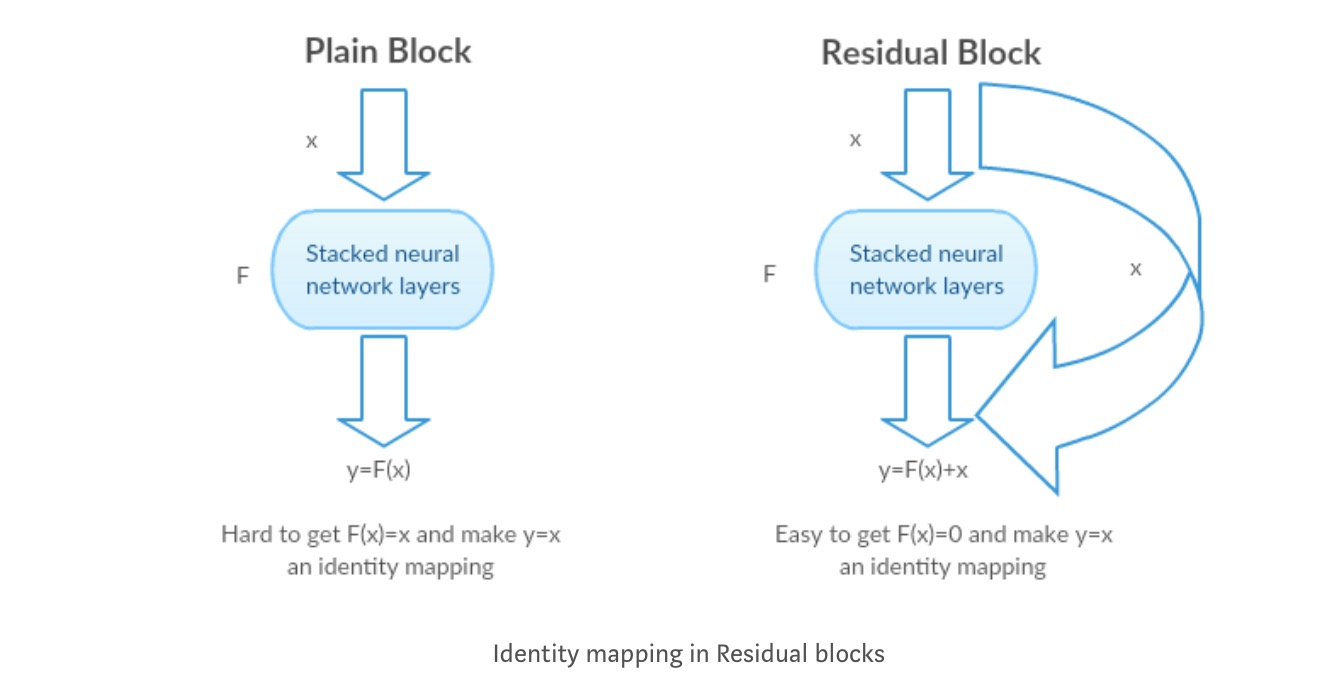
autorii au făcut mai multe teste pentru a-și testa ipoteza. Să ne uităm la fiecare dintre ele acum.

cazuri de testare:

luați o rețea simplă (VGG kind 18 layer network) (rețea-1) și o variantă mai profundă a acesteia (34-strat, rețea-2) și adăugați straturi reziduale la rețea-2 (34 strat cu conexiuni reziduale, rețea-3).

proiectarea rețelei:

1. utilizați 3*3 filtre cea mai mare parte.
2. eșantionare în jos cu straturi CNN cu pas 2.
3. strat global mediu de punere în comun și un strat complet conectat 1000-way cu Softmax în cele din urmă.

există două tipuri de conexiuni reziduale:

I. comenzile rapide de identitate () pot fi utilizate direct atunci când intrarea () și ieșirea () au aceleași dimensiuni.

II. când dimensiunile se schimbă, A) comanda rapidă efectuează încă cartografierea identității, cu intrări suplimentare zero căptușite cu dimensiunea mărită. B) comanda rapidă de proiecție este utilizată pentru a se potrivi cu dimensiunea (realizată de 1*1 conv) folosind următoarea formulă

rezultate

chiar dacă rețeaua de 18 straturi este doar subspațiul din rețeaua de 34 de straturi, aceasta funcționează mai bine. ResNet depășește cu o marjă semnificativă în cazul în care rețeaua este mai profundă

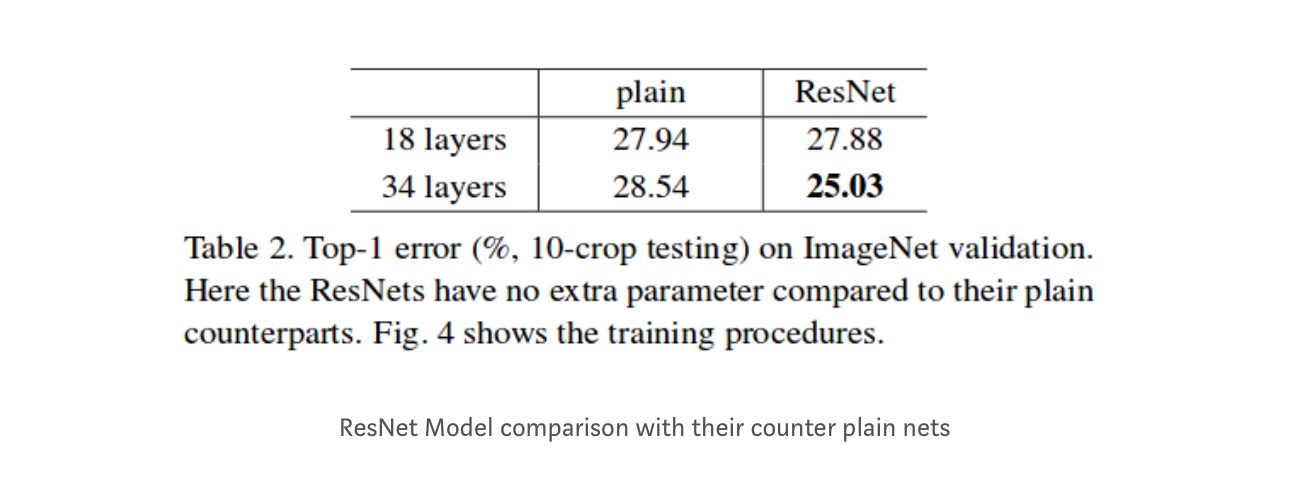
studii mai profunde

Mai mult, sunt studiate mai multe rețele:

fiecare bloc ResNet are fie adâncime de 2 straturi în rețele mici precum resnet 18, 34) sau 3 straturi adânci (resnet 50, 101, 152).

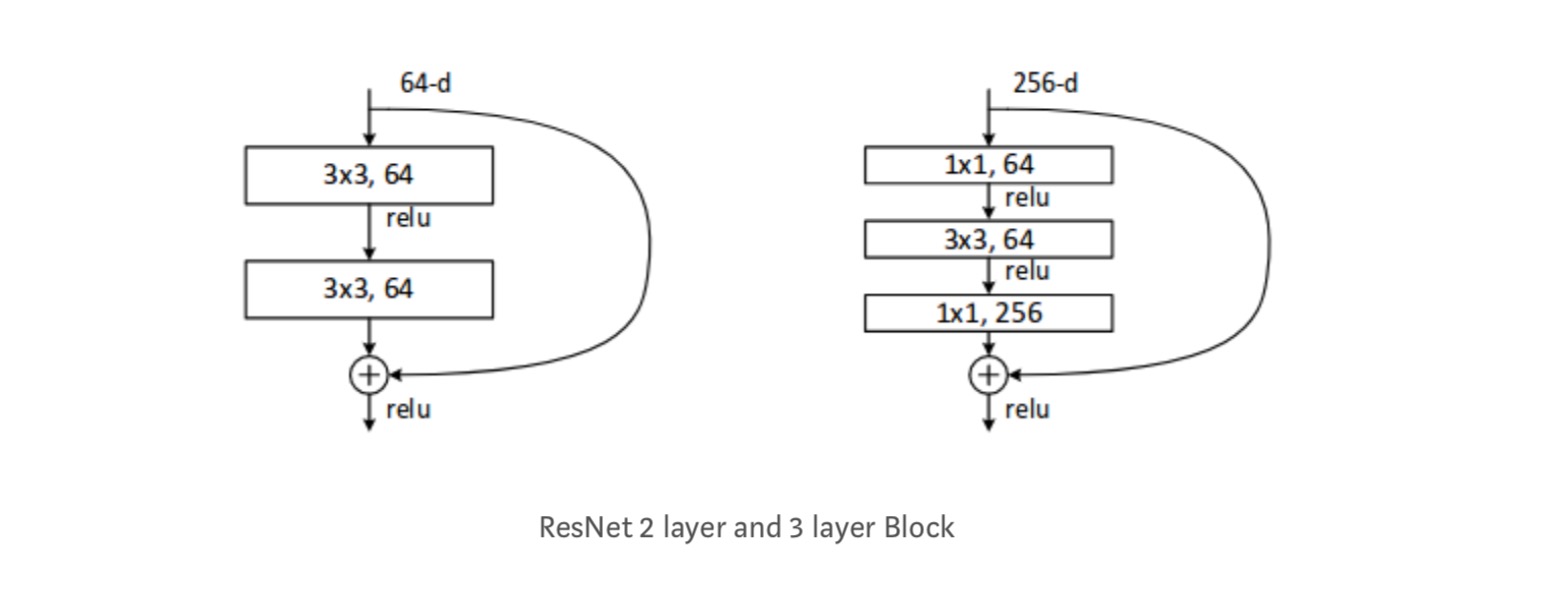
observații

1. rețeaua ResNet converge mai repede în comparație cu o parte simplă a acesteia.
2. identitate vs shorcuts de proiecție. Câștiguri incrementale foarte mici folosind comenzi rapide de proiecție (ecuația-2) în toate straturile. Deci, toate blocurile ResNet utilizează numai comenzi rapide de identitate cu proiecții comenzi rapide utilizate numai atunci când dimensiunile se schimbă.
3. ResNet – 34 a obținut o eroare de validare top-5 cu 5,71% mai bună decât BN-inception și VGG. ResNet-152 realizează o eroare de validare top-5 de 4,49%. Un ansamblu de 6 modele cu adâncimi diferite realizează o eroare de validare top-5 de 3,57%. Câștigarea locului 1 în ILSVRC-2015

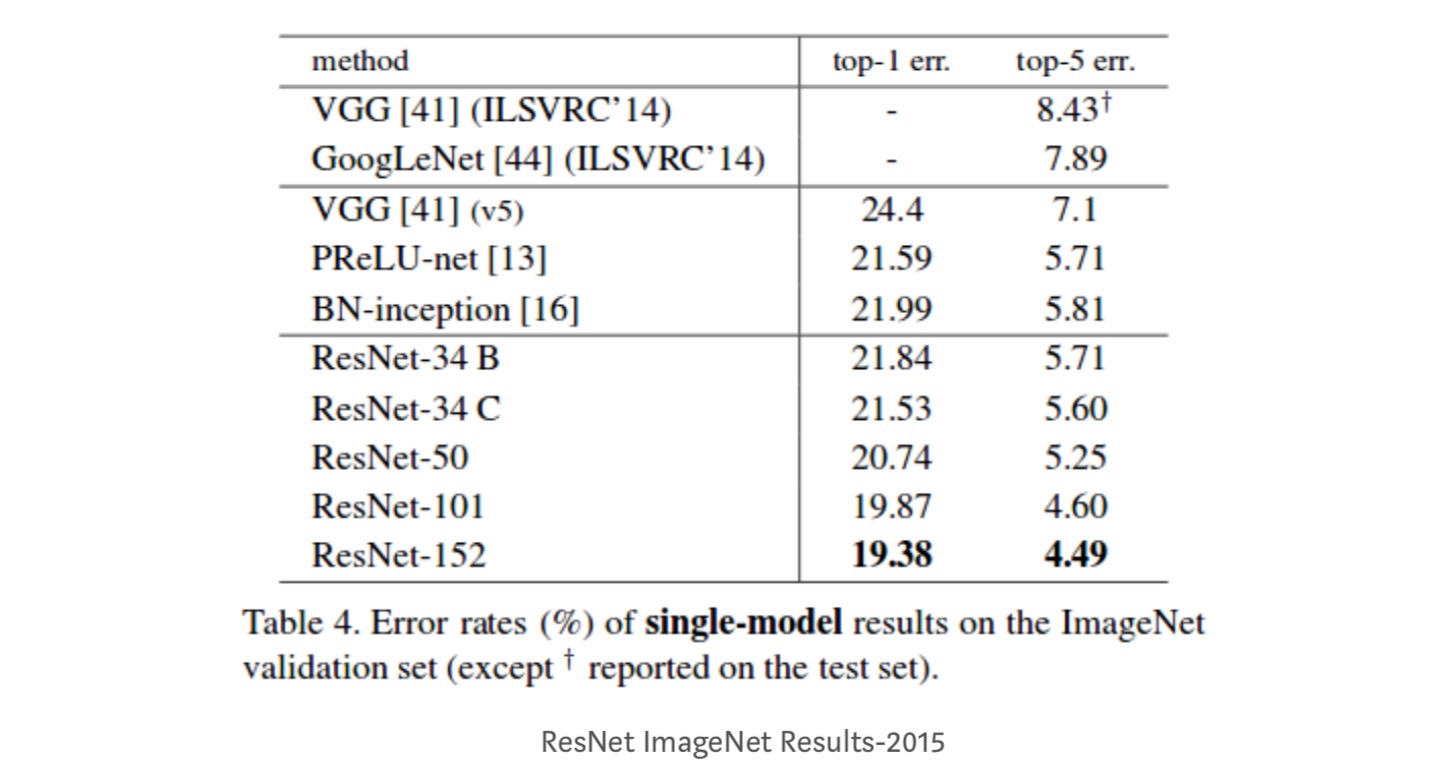
mapări de identitate în rețele reziduale profunde

această lucrare oferă înțelegerea teoretică a motivului pentru care problema gradientului de dispariție nu este prezentă în rețelele reziduale și rolul conexiunilor skip (conexiunile skip înseamnă intrarea sau ) prin înlocuirea mapării identității (x) cu funcții diferite.

Introducere

rețelele reziduale profunde constau din mai multe „unități reziduale”stivuite. Fiecare unitate poate fi exprimată într-o formă generală:

unde și sunt intrarea și ieșirea unității și este o funcție reziduală. În ultima lucrare, este o cartografiere de identitate și este o funcție ReLU.

ideea centrală a Resnet-urilor este de a învăța funcția reziduală aditivă cu privire la , cu o alegere cheie de utilizare a unei cartografieri de identitate . Acest lucru se realizează prin atașarea unei conexiuni de omitere a identității („comandă rapidă”).

în această lucrare, analizăm rețelele reziduale profunde concentrându — ne pe crearea unei căi „directe” pentru propagarea informațiilor-nu numai în cadrul unei unități reziduale, ci prin întreaga rețea. Derivările noastre arată că, dacă ambele și sunt mapări de identitate, semnalul ar putea fi propagat direct de la o unitate la orice alte unități, atât în treceri înainte, cât și înapoi. Experimentele noastre arată empiric că instruirea în general devine mai ușoară atunci când arhitectura este mai aproape de cele două condiții de mai sus.

pentru a înțelege rolul conexiunilor skip, analizăm și comparăm diferite tipuri de . Constatăm că cartografierea identității aleasă în ultima lucrare realizează cea mai rapidă reducere a erorilor și cea mai mică pierdere de antrenament dintre toate variantele pe care le-am investigat, în timp ce omiterea conexiunilor de scalare, închidere și convoluții de 1 Circus 1 conduc la pierderi și erori de antrenament mai mari. Aceste experimente sugerează că păstrarea unei căi de informații” curate ” este utilă pentru facilitarea optimizării.

pentru a construi o cartografiere a identității , vedem funcțiile de activare (ReLU și BN) ca „pre-activare” a straturilor de greutate, spre deosebire de înțelepciunea convențională a „post-activare”. Acest punct de vedere conduce la un nou design al unității reziduale, prezentat în figura următoare. Pe baza acestei unități, prezentăm rezultate competitive pe CIFAR-10/100 cu un ResNet de 1001 straturi, care este mult mai ușor de antrenat și generalizează mai bine decât ResNet-ul original. Raportăm în continuare rezultate îmbunătățite pe ImageNet folosind un ResNet de 200 de straturi, pentru care omologul ultimei lucrări începe să se suprapună. Aceste rezultate sugerează că există mult spațiu pentru a exploata dimensiunea adâncimii rețelei, o cheie a succesului învățării profunde moderne.

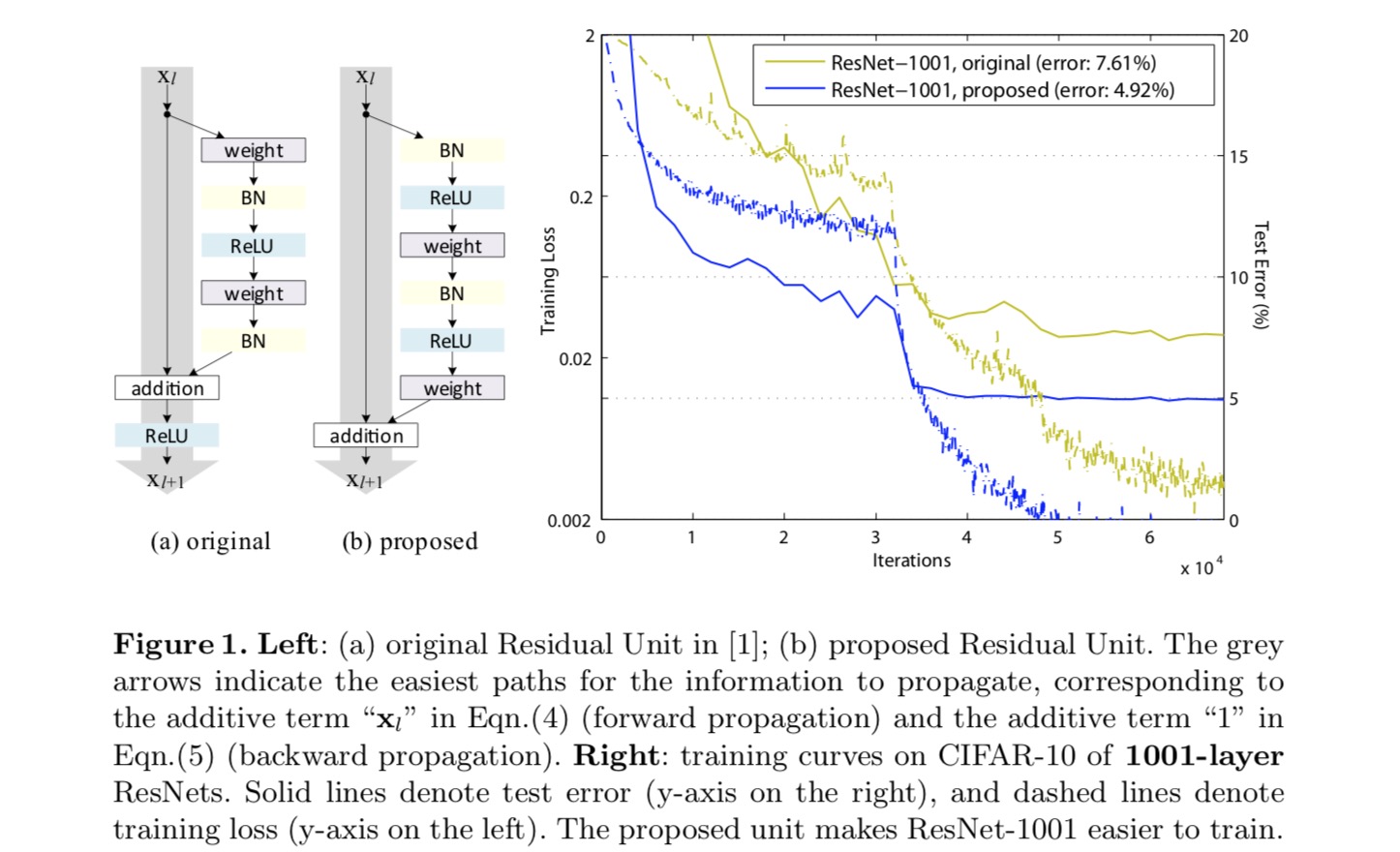
analiza rețelelor reziduale profunde

Resneturile dezvoltate în ultima lucrare sunt arhitecturi modularizate care stivuiesc blocuri de construcție de aceeași formă de conectare. În această lucrare numim aceste blocuri „unități reziduale”. Unitatea reziduală originală din ultima lucrare efectuează următorul calcul:

aici este caracteristica de intrare a unității reziduale. este un set de greutăți (și prejudecăți) asociate cu-Lea unitate reziduală, și este numărul de straturi într-o unitate reziduală ( este 2 sau 3 în ultima lucrare). denotă funcția reziduală, e.g., un teanc de două straturi convoluționale de 3,3 x,3 în ultima lucrare. Funcția este operația după adăugarea element înțelept, și în ultima lucrare este ReLU. Funcția este setată ca o cartografiere a identității:.

dacă este și o cartografiere a identității: , putem obține:

recursiv vom avea:

pentru orice unitate mai adâncă și pentru orice unitate mai puțin adâncă . Această ecuație prezintă unele frumoaseproprietăți. (1) caracteristica oricărei unități mai profunde poate fi reprezentată ca caracteristică a oricărei unități mai puțin adânci plus o funcție reziduală sub formă de , indicând faptul că modelul este într-un mod rezidual între orice unități și . (2) caracteristica , a oricărei unități profunde , este însumarea ieșirilor tuturor funcțiilor reziduale precedente (plus). Acest lucru este în contrast cu o „rețea simplă” în care o caracteristică este o serie de produse matrice-vector, să zicem, (ignorând BN și ReLU).

ecuația de mai sus duce, de asemenea, la proprietăți frumoase de propagare înapoi. Denotând funcția de pierdere ca , din regula lanțului de backpropagare avem:

ecuația de mai sus indică faptul că gradientul poate fi descompus în doi termeni aditivi: un termen de care propagă informații direct, fără cu privire la orice straturi de greutate, și un alt termen de care se propagă prin straturile de greutate. Termenul aditiv al asigură că informațiile sunt propagate direct înapoi la orice unitate mai puțin adâncă l. ecuația de mai sus sugerează, de asemenea, că este puțin probabil ca gradientul să fie anulat pentru un mini-lot, deoarece, în general, termenul nu poate fi întotdeauna -1 pentru toate probele dintr-un mini-lot. Aceasta implică faptul că gradientul unui strat nu dispare chiar și atunci când greutățile sunt arbitrar de mici.cele două ecuații de mai sus sugerează că semnalul poate fi propagat direct de la orice unitate la alta, atât înainte, cât și înapoi. Fundamentul primelor două ecuații de mai sus este două mapări de identitate: (1) conexiunea de omitere a identității și (2) condiția care este o cartografiere a identității.

importanța identității sări peste conexiuni

să luăm în considerare o modificare simplă, , pentru a rupe comanda rapidă de identitate:

unde este un scalar modulator (pentru simplitate încă presupunem că este identitate). Aplicând recursiv această formulare obținem o ecuație similară cu cea de mai sus:

unde notația absoarbe scalarii în funcțiile reziduale. În mod similar, avem backpropagation de următoarea formă:

spre deosebire de ecuația anterioară, în această ecuație primul termen aditiv este modulat de un factor . Pentru o rețea extrem de profundă ( este mare), dacă pentru toți , acest factor poate fi exponențial mare; dacă pentru toți , acest factor poate fi exponențial mic și dispare, ceea ce blochează semnalul inversat din scurtătură și îl obligă să curgă prin straturile de greutate. Acest lucru duce la dificultăți de optimizare așa cum arătăm prin experimente.

în analiza de mai sus, conexiunea inițială de ignorare a identității este înlocuită cu o scalare simplă . În cazul în care conexiunea skip reprezintă transformări mai complicate (cum ar fi gating și 1 circt 1 convoluții), în ecuația de mai sus primul termen devine unde este derivata . Acest produs poate, de asemenea, să împiedice propagarea informațiilor și să împiedice procedura de instruire, așa cum s-a văzut în următoarele experimente.

experimente pe conexiuni Skip

experimentăm cu ResNet 110 straturi pe CIFAR-10. Acest ResNet-110 extrem de profund are 54 de unități reziduale cu două straturi (constând din 3 straturi convoluționale 3) și este o provocare pentru optimizare. Sunt experimentate diferite tipuri de conexiuni de omitere. Vedeți figura următoare:

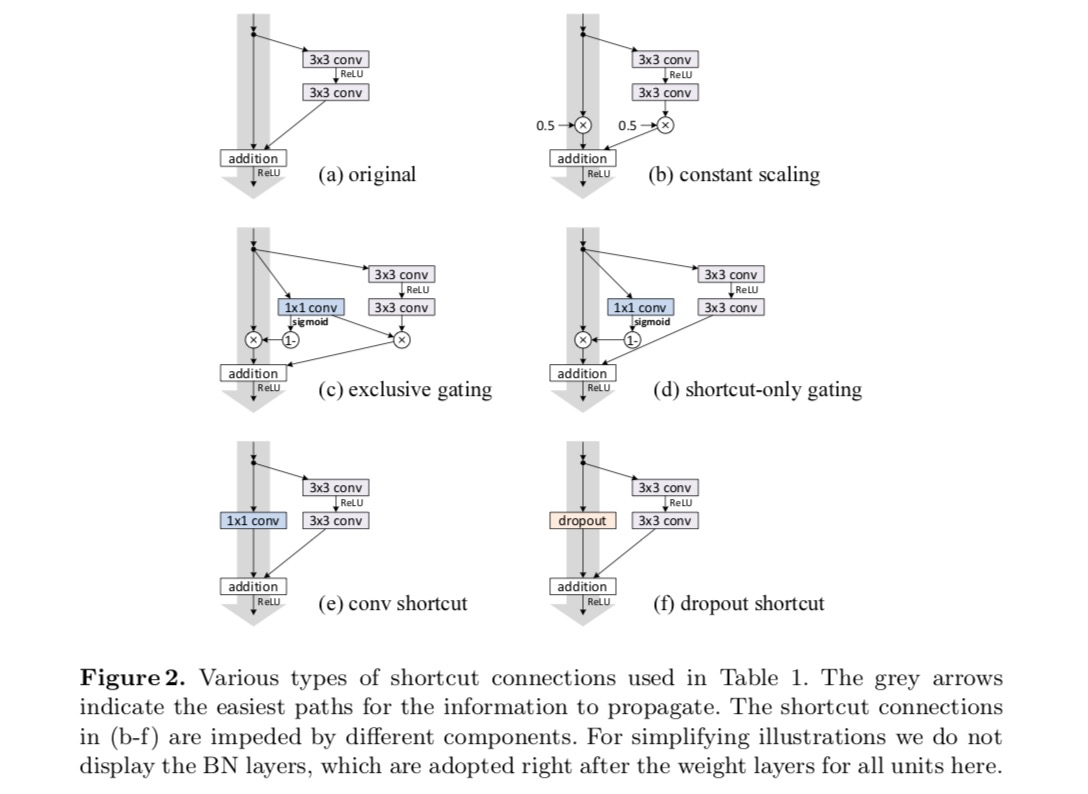
rezultatele clasificării sunt afișate în tabelul următor:

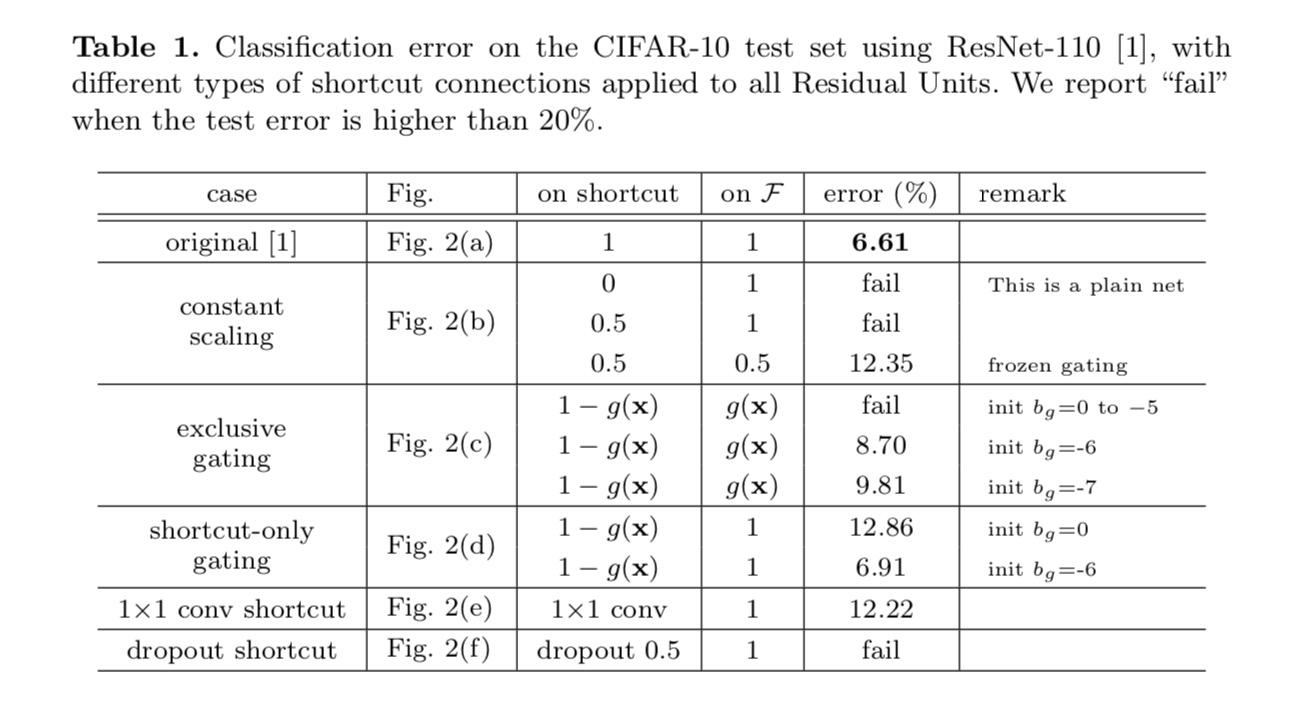
după cum este indicat de săgețile gri din figura de mai sus, conexiunile de comenzi rapide sunt căile cele mai directe pentru propagarea informațiilor. Manipulările Multiplicative (scalare, închidere, convoluții de la 1 la 1 și abandon) pe scurtături pot împiedica propagarea informațiilor și pot duce la probleme de optimizare.

este demn de remarcat faptul că scurtăturile convoluționale de la gating și de la 1 int 1 introduc mai mulți parametri și ar trebui să aibă abilități de reprezentare mai puternice decât scurtăturile de identitate. De fapt, închiderea numai pentru comenzi rapide și convoluția 1 de la 1 la 1 acoperă spațiul de soluție al comenzilor rapide de identitate (adică ar putea fi optimizate ca comenzi rapide de identitate). Cu toate acestea, eroarea lor de antrenament este mai mare decât cea a comenzilor rapide de identitate, indicând faptul că degradarea acestor modele este cauzată de probleme de optimizare, în loc de abilități de reprezentare.

utilizarea funcțiilor de activare

experimentele din secțiunea de mai sus presupun că activarea după adăugare este maparea identității. Dar, în experimentele de mai sus este ReLU așa cum este proiectat în prima lucrare. În continuare vom investiga impactul .

dorim să realizăm o mapare a identității, care se realizează prin rearanjarea funcțiilor de activare (ReLU și / sau BN, normalizarea lotului). În figura următoare, unitatea reziduală originală din ultima hârtie are o formă în Fig. 4(a) – BN este utilizat după fiecare strat de greutate, iar ReLU este adoptat după BN, cu excepția faptului că ultimul ReLU dintr-o unitate reziduală este după adăugarea elementwise ( = ReLU). Fig. 4 (b-e) arătați alternativele pe care le-am investigat.

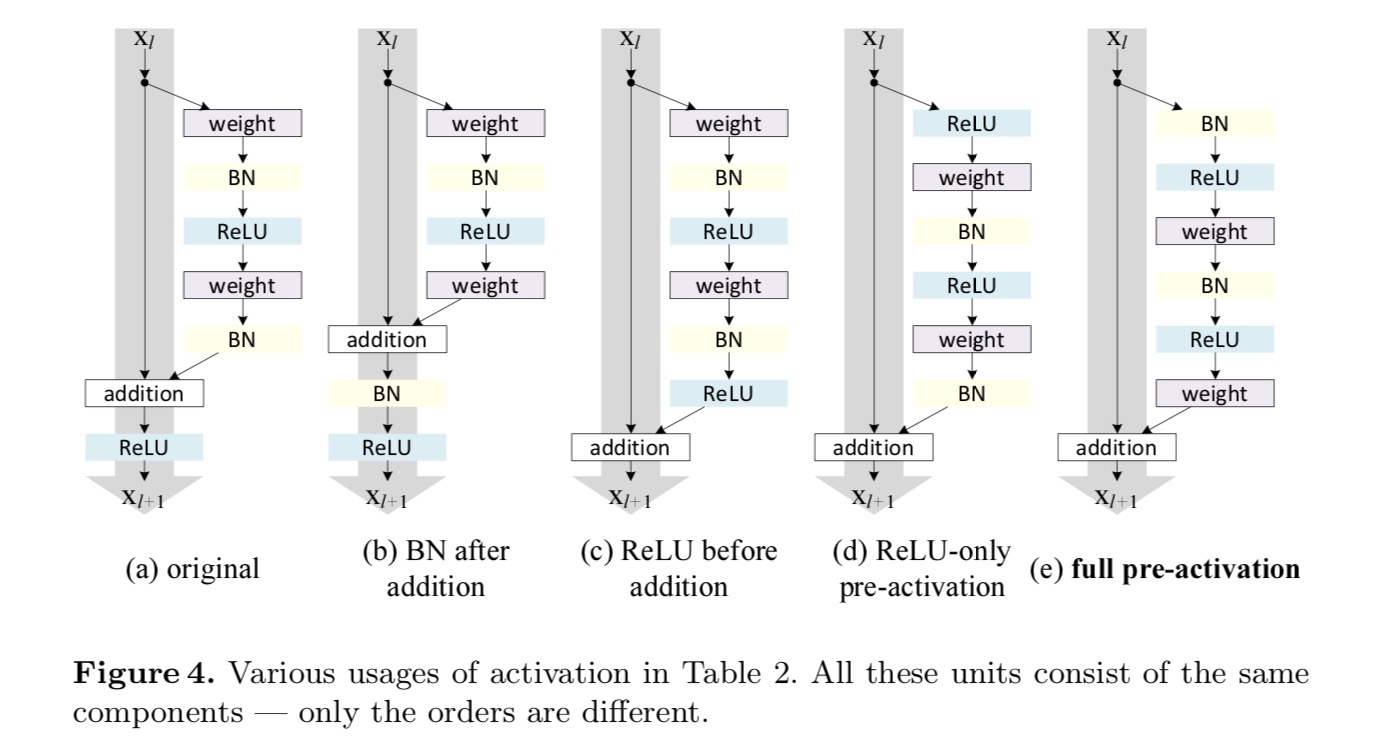
experimente privind activarea

în această secțiune experimentăm cu ResNet-110 și o arhitectură de blocaj cu 164 de straturi (notată ca ResNet-164). O unitate reziduală de strangulare constă dintr-un strat de 1 hectar 1 pentru reducerea dimensiunii, un strat de 3 centar 3, și un strat de 1 centar 1 pentru refacerea dimensiunii. Așa cum a fost proiectat în ultima lucrare, complexitatea sa de calcul este similară cu unitatea reziduală de două 3-3.

Post-activare sau pre-activare?

în designul original, activarea afectează ambele căi în următoarea unitate reziduală: . În continuare dezvoltăm o formă asimetrică în care o activare afectează doar calea: , pentru oricare . Prin redenumirea notațiilor, avem următoarea formă:

pentru această nouă unitate reziduală ca în ecuația de mai sus, Noua activare după adăugare devine o cartografiere a identității. Acest design înseamnă că, dacă o nouă activare după adăugare este adoptată asimetric, aceasta este echivalentă cu reformarea ca preactivare a următoarei unități reziduale. Acest lucru este ilustrat în figura următoare:

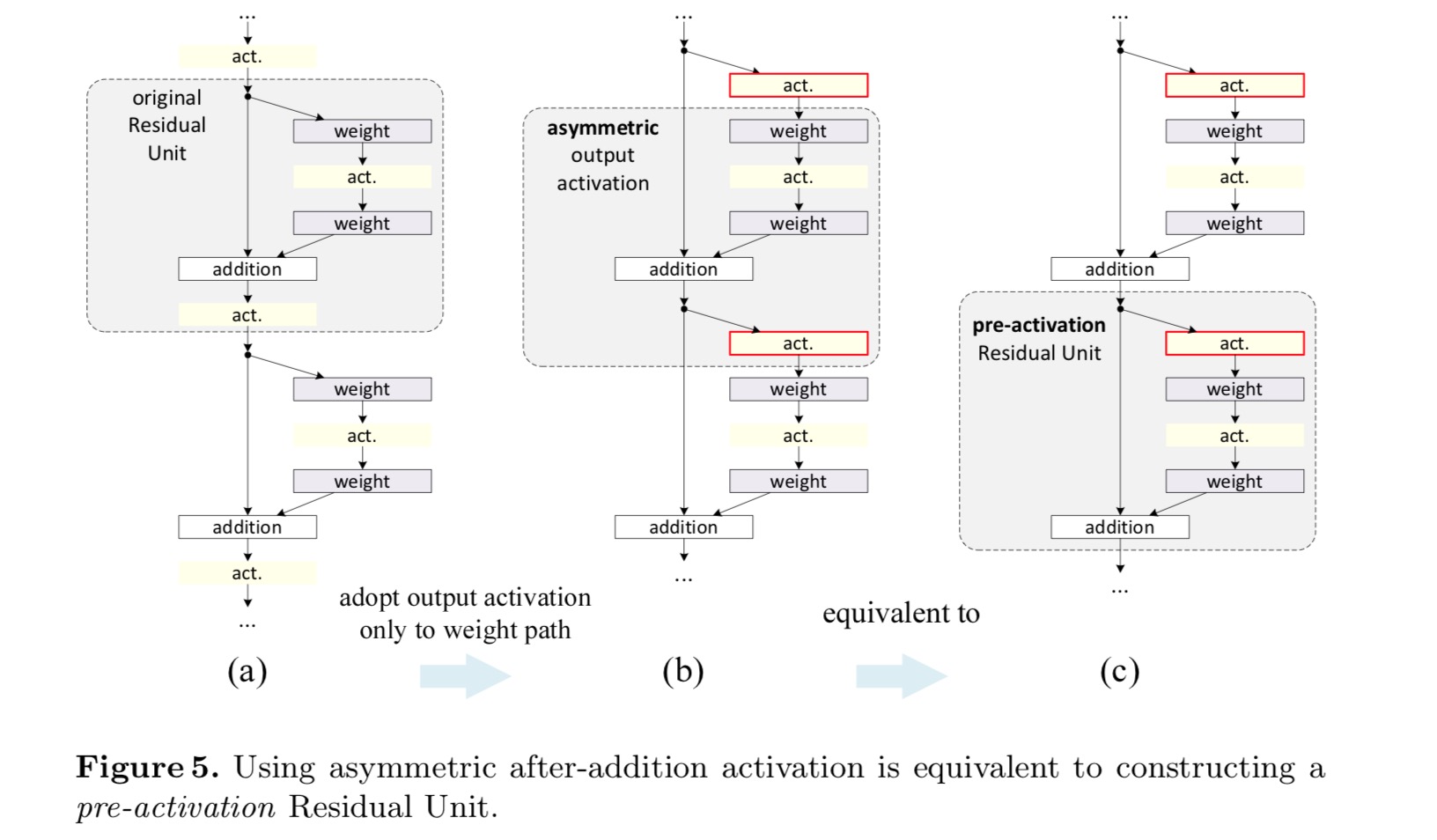
distincția dintre post-activare / pre-activare este cauzată de prezența adăugării elementului. Pentru o rețea simplă care are n straturi, există activări N – 1 (bn / ReLU) și nu contează dacă ne gândim la ele ca la post-sau pre-activări. Dar pentru straturile ramificate îmbinate prin adăugare, poziția activării contează. Diferitele utilizări ale activării sunt afișate în Figura 4.

experimentăm cu două astfel de modele: (1) preactivarea numai ReLU și (2) preactivarea completă în cazul în care BN și ReLU sunt ambele adoptate înainte de straturile de greutate. Într-un fel surprinzător, atunci când bn și ReLU sunt ambele utilizate ca pre-activare, rezultatele sunt îmbunătățite prin marje sănătoase

descoperim că impactul pre-activării este dublu. În primul rând, optimizarea este facilitată în continuare (comparativ cu ResNet de bază) deoarece f este o cartografiere a identității. În al doilea rând, utilizarea BN ca pre-activare îmbunătățește regularizarea modelelor.

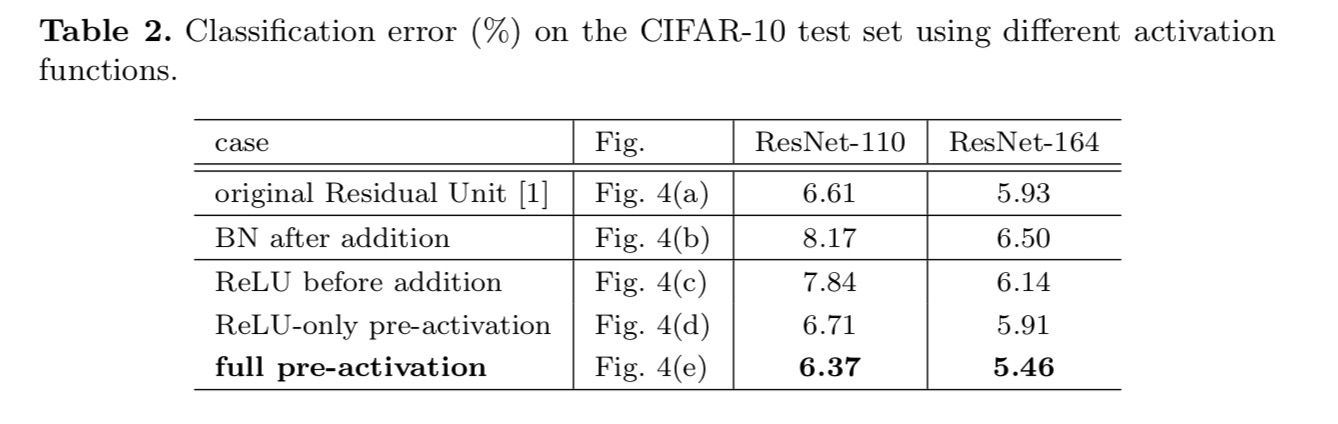
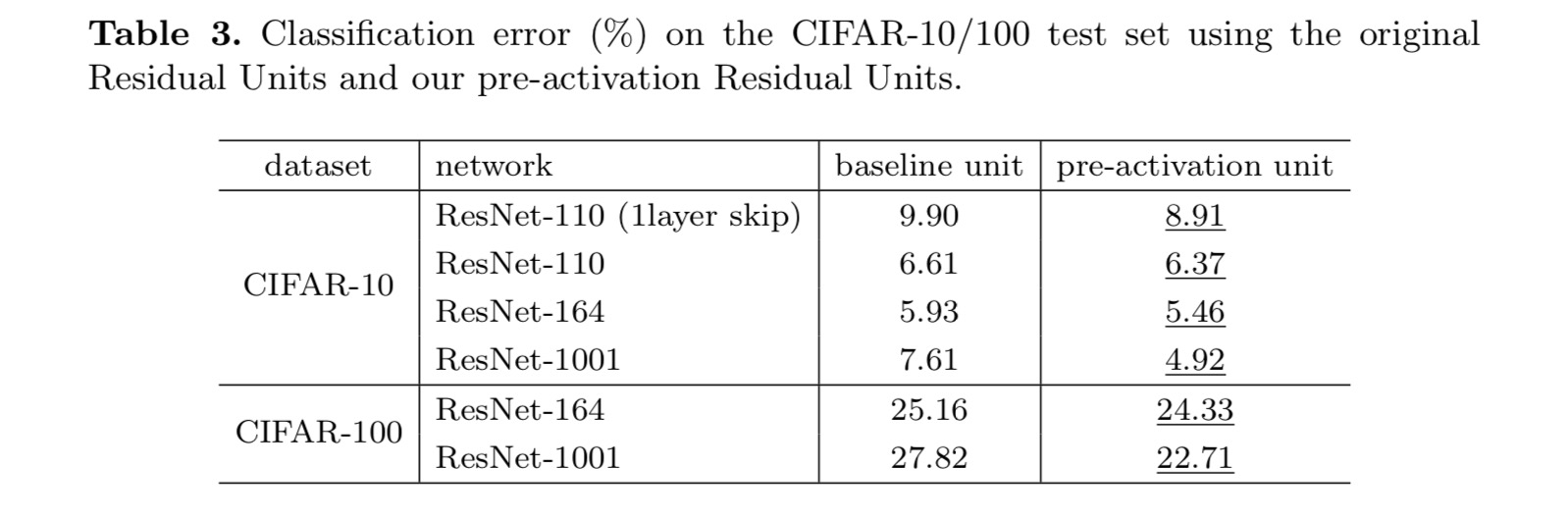
concluzie

această lucrare investighează formulările de propagare din spatele mecanismelor de conectare a rețelelor reziduale profunde. Derivările noastre implică faptul că conexiunile de scurtă durată ale identității și activarea identității după adăugare sunt esențiale pentru buna propagare a informațiilor. Experimentele de ablație demonstrează fenomene care sunt în concordanță cu derivările noastre. De asemenea, prezentăm rețele profunde de 1000 de straturi care pot fi ușor instruite și pot obține o precizie îmbunătățită.

transformare reziduală agregată pentru rețele neuronale profunde

Introducere

cercetarea privind recunoașterea vizuală trece printr-o tranziție de la „ingineria caracteristicilor” la „ingineria rețelei”. Efortul uman a fost mutat la proiectarea arhitecturilor de rețea mai bune pentru învățarea reprezentărilor.

proiectarea arhitecturilor devine din ce în ce mai dificilă odată cu creșterea numărului de hiper-parametri, mai ales atunci când există mai multe straturi. Rețelele VGG prezintă o strategie simplă, dar eficientă, de construire a rețelelor foarte adânci: stivuirea blocurilor de aceeași formă. Această strategie este moștenită de Resnet-uri care stivă module de aceeași topologie. Această regulă simplă reduce alegerile libere ale hiper-parametrilor, iar adâncimea este expusă ca o dimensiune esențială în rețelele neuronale. Mai mult, susținem că simplitatea acestei reguli poate reduce riscul de adaptare excesivă a hiperparametrilor la un set de date specific. Robustețea rețelelor VGG și a Resnet-urilor a fost dovedită prin diferite sarcini de recunoaștere vizuală și prin sarcini non-vizuale care implică vorbire și limbaj.spre deosebire de rețelele VGG, familia modelelor inițiale a demonstrat că topologiile atent proiectate sunt capabile să obțină o precizie convingătoare cu o complexitate teoretică scăzută. Modelele inițiale au evoluat de-a lungul timpului, dar o proprietate comună importantă este o strategie split-transform-merge. Într-un modul Inception, intrarea este împărțită în câteva încorporări de dimensiuni inferioare (prin convoluții de la 1 la 1 la 1), transformate de un set de filtre specializate (3 la 3, 5 la 5 la 5 etc.), și fuzionat prin concatenare. Comportamentul split-transform-merge al modulelor inițiale este de așteptat să se apropie de puterea de reprezentare a straturilor mari și dense, dar la o complexitate de calcul considerabil mai mică.

În ciuda preciziei bune, realizarea modelelor inițiale a fost însoțită de o serie de factori complicatori. Deși combinațiile atente ale acestor componente produc rețete excelente de rețea neuronală, în general nu este clar cum să se adapteze arhitecturile inițiale la noile seturi de date/sarcini, mai ales atunci când există mulți factori și hiper-parametri care trebuie proiectați.

în această lucrare, prezentăm o arhitectură simplă care adoptă strategia VGG / ResNets de repetare a straturilor, exploatând în același timp strategia split-transform-merge într-un mod ușor, extensibil. Un modul din rețeaua noastră efectuează un set de transformări, fiecare pe o încorporare cu dimensiuni reduse, ale cărei ieșiri sunt agregate prin însumare. Urmărim o simplă realizare a acestei idei — transformările care trebuie agregate sunt toate de aceeași topologie. Acest design ne permite să ne extindem la orice număr mare de transformări fără modele specializate.

demonstrăm empiric că transformările noastre agregate depășesc modulul ResNet original, chiar și în condițiile restrânse de menținere a complexității computaționale și a dimensiunii modelului. Subliniem că, deși este relativ ușor să crești precizia prin creșterea capacității (mergând mai adânc sau mai larg), metodele care cresc precizia menținând (sau reducând) complexitatea sunt rare în literatură.

metoda noastră indică faptul că cardinalitatea (dimensiunea setului de transformări) este o dimensiune concretă, măsurabilă, care are o importanță centrală, pe lângă dimensiunile lățimii și adâncimii. Experimentele demonstrează că creșterea cardinalității este o modalitate mai eficientă de a obține precizie decât de a merge mai adânc sau mai larg, mai ales atunci când adâncimea și lățimea încep să dea randamente în scădere pentru modelele existente.

rețelele noastre neuronale, denumite ResNeXt (sugerând următoarea dimensiune), depășesc ResNet-101/152, ResNet-200, Inception-v3 și Inception-ResNet-v2 în setul de date de clasificare ImageNet. În special, un ResNeXt cu 101 straturi este capabil să obțină o precizie mai bună decât ResNet-200, dar are doar 50% complexitate. Mai mult, ResNeXt prezintă modele considerabil mai simple decât toate modelele Inception.

metoda

adoptăm un design foarte modularizat după VGG / ResNets. Rețeaua noastră constă dintr-un teanc de blocuri reziduale. Aceste blocuri au aceeași topologie și sunt supuse a două reguli simple inspirate de VGG/ResNets: (1) dacă produc hărți spațiale de aceeași dimensiune, blocurile împărtășesc aceiași hiper-parametri (lățimea și dimensiunile filtrului) și (2) de fiecare dată când harta spațială este redusă cu un factor de 2, lățimea blocurilor este înmulțită cu un factor de 2. A doua regulă asigură că complexitatea computațională, în termeni de FLOPs (operații în virgulă mobilă, în #de înmulțire-adăugări), este aproximativ aceeași pentru toate blocurile.

cu aceste două reguli, trebuie doar să proiectăm un modul șablon și toate modulele dintr-o rețea pot fi determinate în consecință. Deci, aceste două reguli restrâng foarte mult spațiul de proiectare și ne permit să ne concentrăm asupra câtorva factori cheie. Rețelele construite prin aceste reguli sunt în tabelul 1.

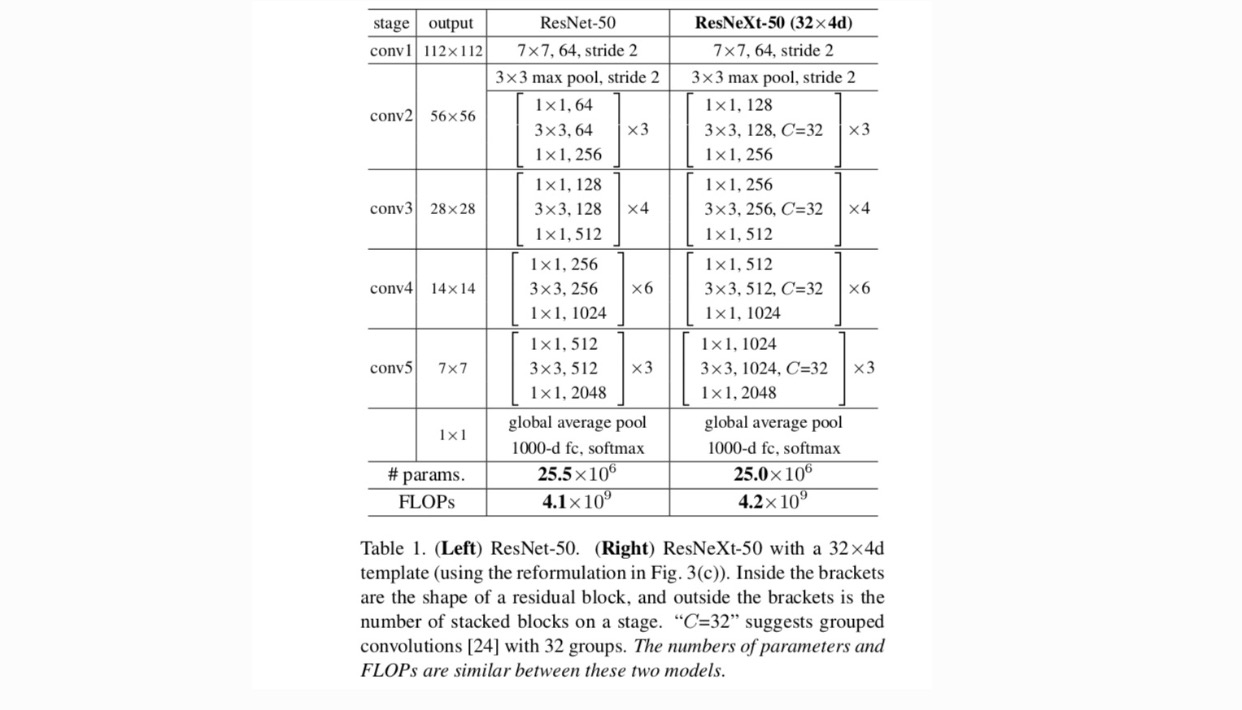
cei mai simpli neuroni din rețelele neuronale artificiale realizează produsul interior (suma ponderată), care este transformarea elementară realizată de straturi complet conectate și convoluționale.

operația de mai sus poate fi reformată ca o combinație de divizare, transformare și agregare. (1): divizare: vectorul este feliat ca o încorporare cu dimensiuni reduse, iar în cele de mai sus, este un subspațiu cu o singură dimensiune (2) transformare: reprezentarea cu dimensiuni reduse este transformată, iar în cele de mai sus, este pur și simplu scalată: (3) agregare: transformările din toate încorporările sunt agregate de .având în vedere analiza de mai sus a unui neuron simplu, considerăm înlocuirea transformării elementare (w_i, x_i) cu o funcție mai generică, care în sine poate fi și o rețea. În mod formal, prezentăm transformări agregate ca:

unde poate fi o funcție arbitrară. Analog unui neuron simplu, ar trebui să se proiecteze într-o încorporare (opțional cu dimensiuni reduse) și apoi să o transforme.

ne referim la cardinalitate. este într-o poziție similară cu în , dar nu au nevoie de egal și poate fi un număr arbitrar. Arătăm prin experimente că cardinalitatea este o dimensiune esențială și poate fi mai eficientă decât dimensiunile lățimii și adâncimii.

în această lucrare, considerăm o modalitate simplă de proiectare a funcțiilor de transformare: toate au aceeași topologie. Aceasta extinde strategia în stil VGG de repetare a straturilor de aceeași formă. Am setat transformarea individuală să fie arhitectura în formă de blocaj ilustrată în Fig. 1 (dreapta). În acest caz, primul strat de 1 hectolitru 1 din fiecare produce încorporarea cu dimensiuni reduse.

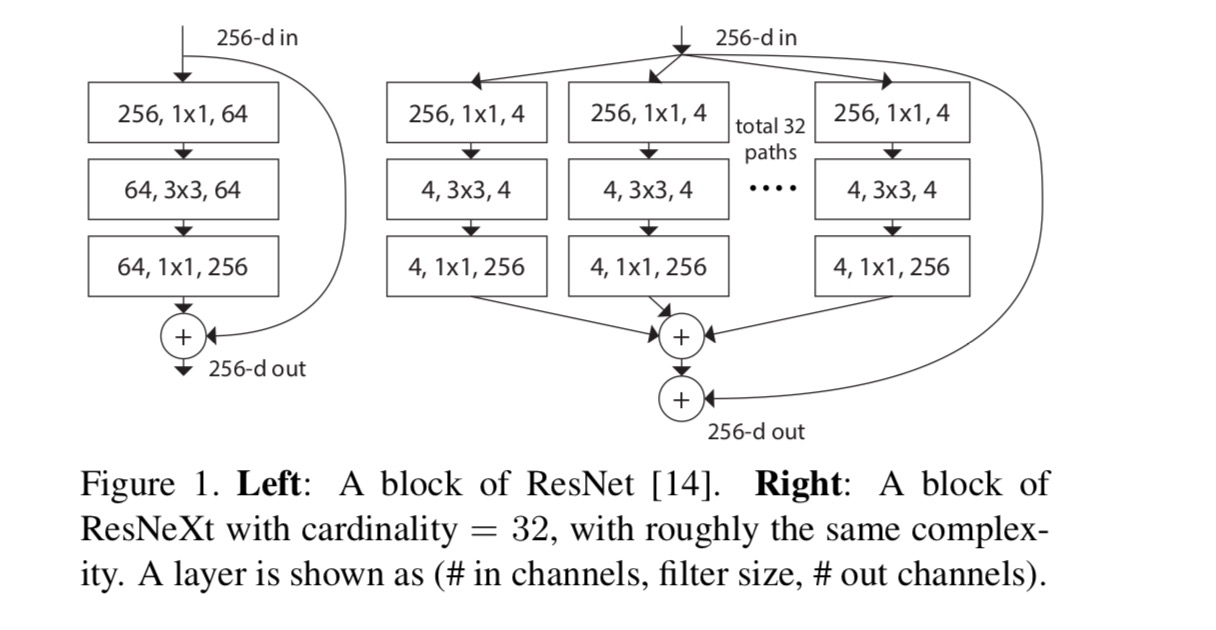
transformarea agregată în ultima ecuație servește ca funcție reziduală:

unde este ieșirea.

relațiile dintre Resnext și Inception-ResNet / Gruped-convoluții sunt prezentate în figura următoare:

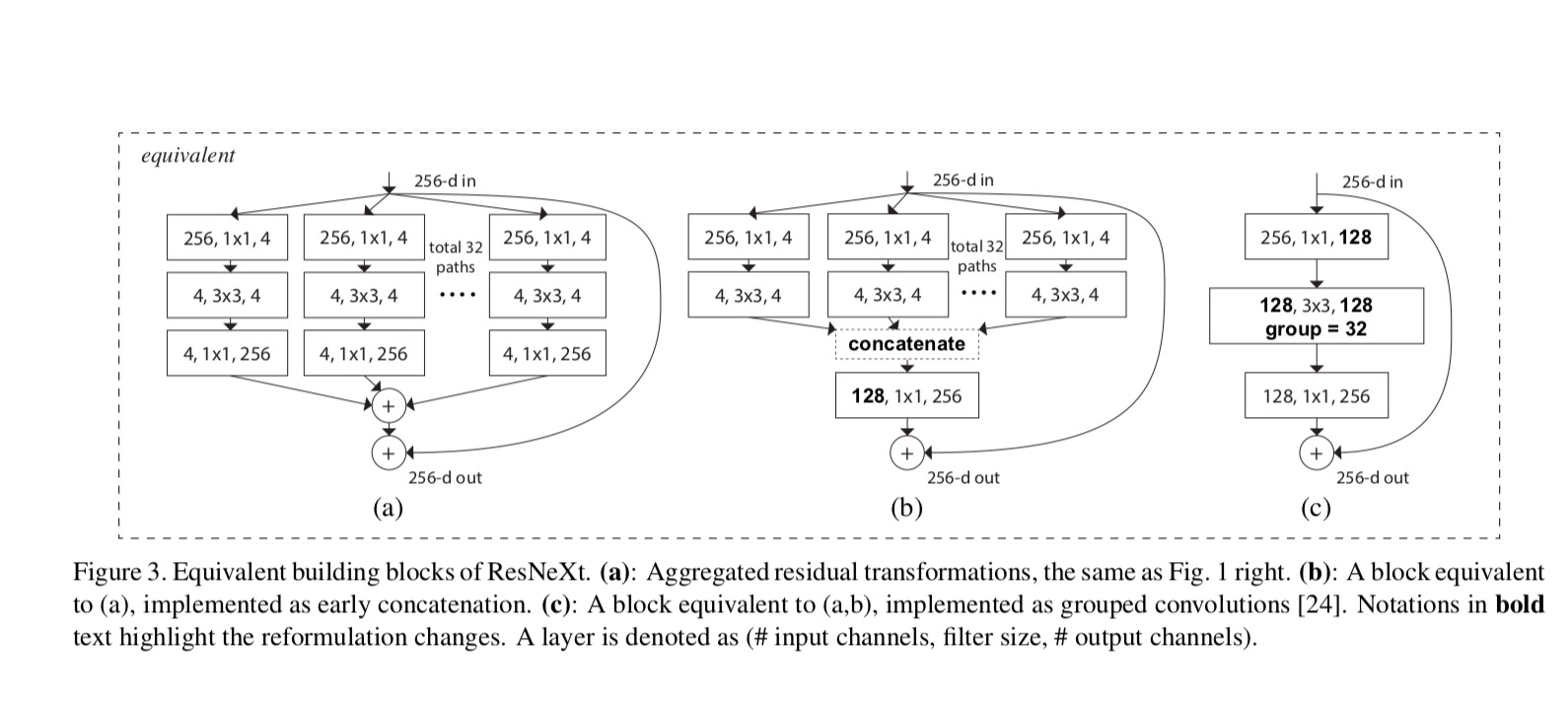
când evaluăm diferite cardinalități păstrând în același timp complexitatea, dorim să minimizăm modificarea altor hiper-parametri. Alegem să reglăm lățimea gâtului (de exemplu, 4-d în Fig 1(dreapta)), deoarece poate fi izolat de intrarea și ieșirea blocului. Această strategie nu introduce nicio modificare a altor hiper-parametri (adâncimea sau lățimea de intrare/ieșire a blocurilor), deci este util pentru noi să ne concentrăm asupra impactului cardinalității.

în Fig. 1 (stânga), blocul original resnet strangulare are parametri și flops proporționale (pe aceeași dimensiune hartă caracteristică). Cu lățimea gâtului, șablonul nostru din Fig. 1 (dreapta) are: parametri și flopuri proporționale. Când și, acest număr . Următorul tabel prezintă relația dintre cardinalitate și lățimea gâtului.

experimente

cardinalitate vs.lățime. Evaluăm mai întâi compromisul dintre cardinalitate și lățimea gâtului, sub complexitatea conservată, așa cum este enumerat în tabelul 2. Tabelul 3 prezintă rezultatele. Comparând cu ResNet-50, 32 4D resnext-50 are o eroare de validare de 22,2%, care este cu 1,7% mai mică decât valoarea de bază a ResNet 23,9%. Cu cardinalitatea crescând de la 1 la 32, păstrând în același timp complexitatea, rata de eroare continuă să se reducă. Mai mult decât atât, 32 4D resnext are, de asemenea, o eroare de antrenament mult mai mică decât Countetpart ResNet, sugerând că câștigurile nu provin din regularizare, ci din reprezentări mai puternice.

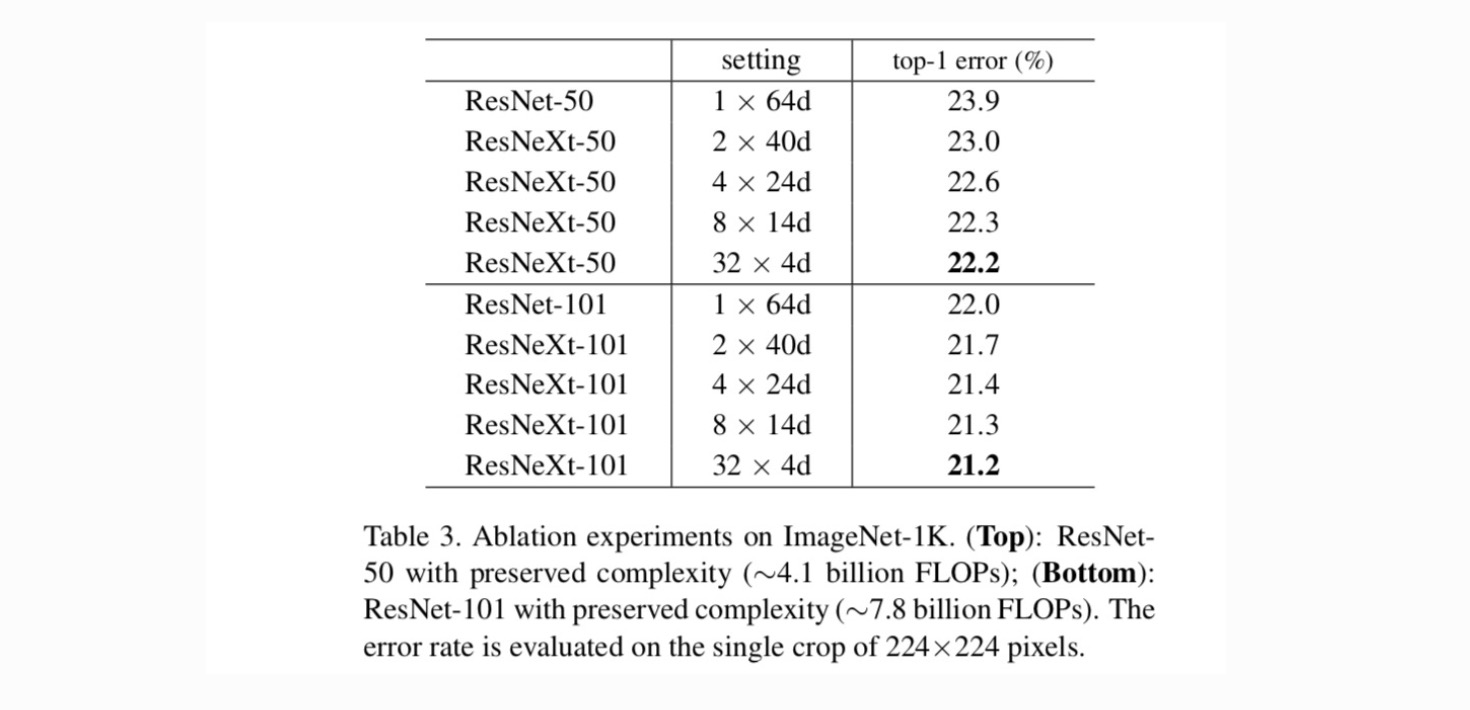
creșterea Cardinalității VS.mai profund / mai larg.

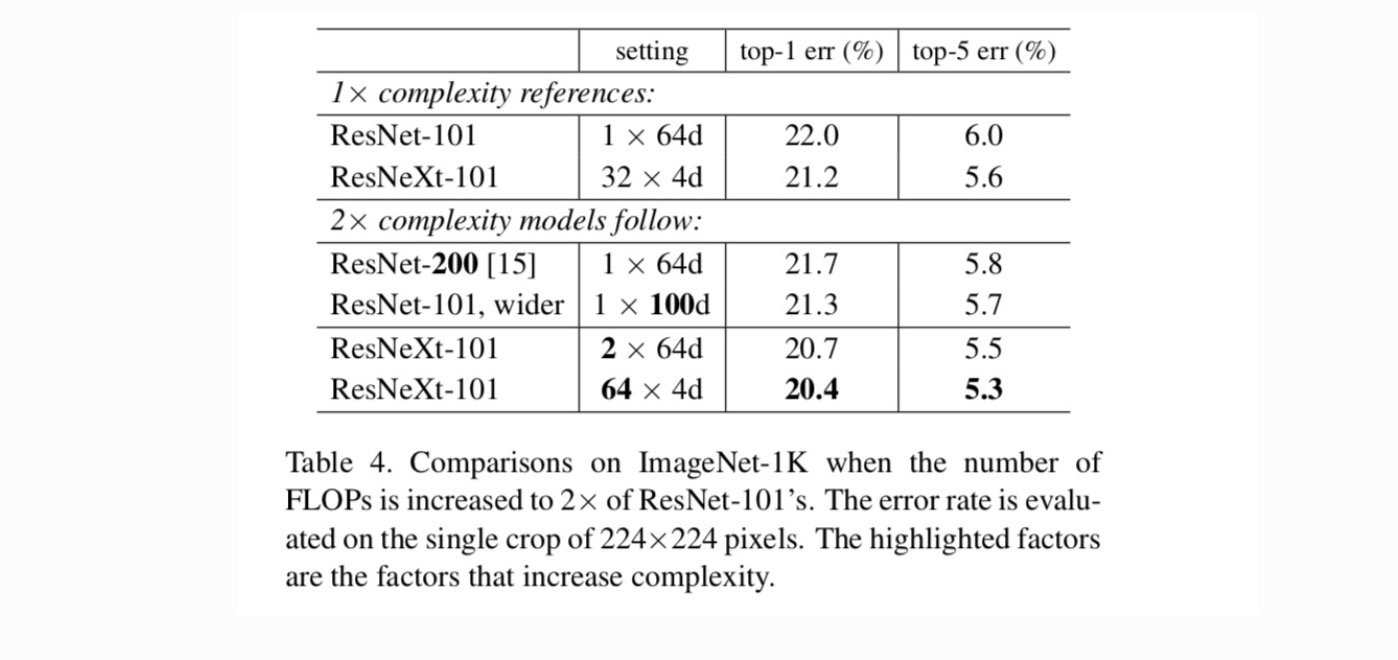
în continuare investigăm creșterea complexității prin creșterea cardinalității C sau creșterea adâncimii sau lățimii. Comparăm următoarele variante (1) Mergând mai adânc la 200 de straturi. Adoptăm ResNet-200. (2) Mergând mai larg prin creșterea lățimii gâtului. (3) Creșterea cardinalității prin dublarea C.

Tabelul 4 arată că o creștere a complexității cu 2% reduce constant eroarea față de valoarea inițială ResNet-101 (22,0%). Dar îmbunătățirea este mică atunci când mergeți mai adânc (ResNet-200, cu 0,3%) sau mai larg (resnet-101 mai larg, cu 0,7%). Dimpotrivă, creșterea cardinalității C arată rezultate mult mai bune decât a merge mai adânc sau mai larg.

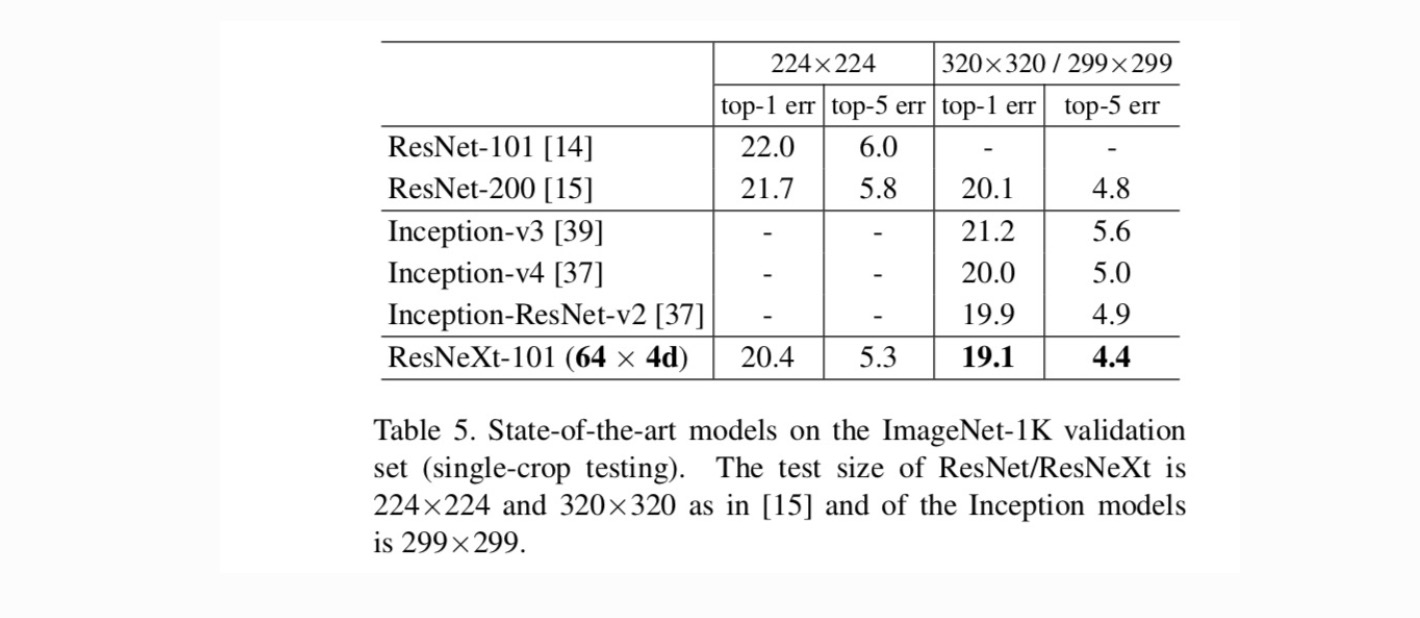
comparații cu rezultate de ultimă generație. Tabelul 5 prezintă mai multe rezultate ale testării unei singure culturi pe setul de validare ImageNet. Rezultatele noastre se compară favorabil cu ResNet, Inception-v3/v4 și Inception-ResNet-v2, obținând o rată de eroare top-5 cu o singură cultură de 4,4%. În plus, designul nostru de arhitectură este mult mai simplu decât toate modelele Inception și necesită mult mai puțini hiper-parametri care trebuie setați manual.