Introducere
analiza componentelor principale (PCA) este un algoritm de reducere a dimensionalității care poate fi utilizat pentru a accelera semnificativ algoritmul de învățare a caracteristicilor nesupravegheate. Mai important, înțelegerea PCA ne va permite să implementăm ulterior albirea, care este un pas important de pre-procesare pentru mulți algoritmi.
Să presupunem că vă antrenați algoritmul pe imagini. Apoi, intrarea va fi oarecum redundantă, deoarece valorile pixelilor adiacenți dintr-o imagine sunt foarte corelate. În mod concret, să presupunem că ne antrenăm pe patch-uri de imagine în tonuri de gri de 16×16. Apoi \textstyle x \ in \ Re^{256} sunt 256 vectori dimensionali, cu o caracteristică \ textstyle x_j corespunzătoare intensității fiecărui pixel. Datorită corelației dintre pixelii adiacenți, PCA ne va permite să aproximăm intrarea cu una mult mai mică dimensională, în timp ce suferim foarte puține erori.
exemplu și fundal matematic
pentru exemplul nostru de rulare, vom folosi un set de date \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} cu \textstyle N=2 intrări dimensionale, astfel încât \textstyle x^{(i)} \în \Re^2. Să presupunem că dorim să reducem datele de la 2 dimensiuni la 1. (În practică, am putea dori să reducem datele de la 256 la 50 de dimensiuni, să zicem; dar utilizarea datelor cu dimensiuni mai mici în exemplul nostru ne permite să vizualizăm mai bine algoritmii.) Iată setul nostru de date:
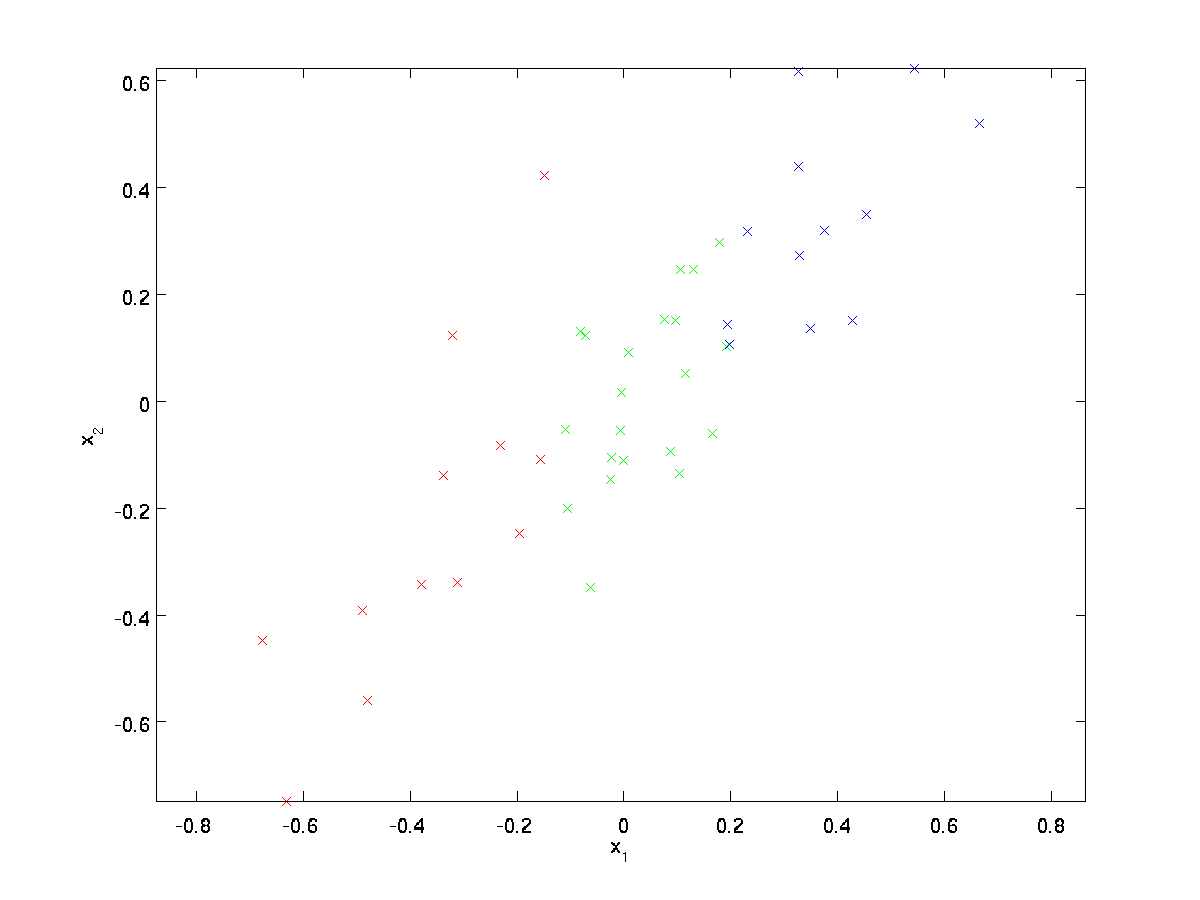
aceste date au fost deja pre-procesate astfel încât fiecare dintre caracteristicile \textstyle x_1 și \textstyle x_2 să aibă aproximativ aceeași medie (zero) și varianță.
în scopul ilustrării, am colorat, de asemenea, fiecare dintre punctele una dintre cele trei culori, în funcție de valoarea lor \ textstyle x_1; aceste culori nu sunt utilizate de algoritm, și sunt doar pentru ilustrare.
PCA va găsi un subspațiu dimensional inferior pe care să proiecteze datele noastre.
din examinarea vizuală a datelor, se pare că \textstyle u_1 este direcția principală de variație a datelor, și \textstyle u_2 direcția secundară de variație:
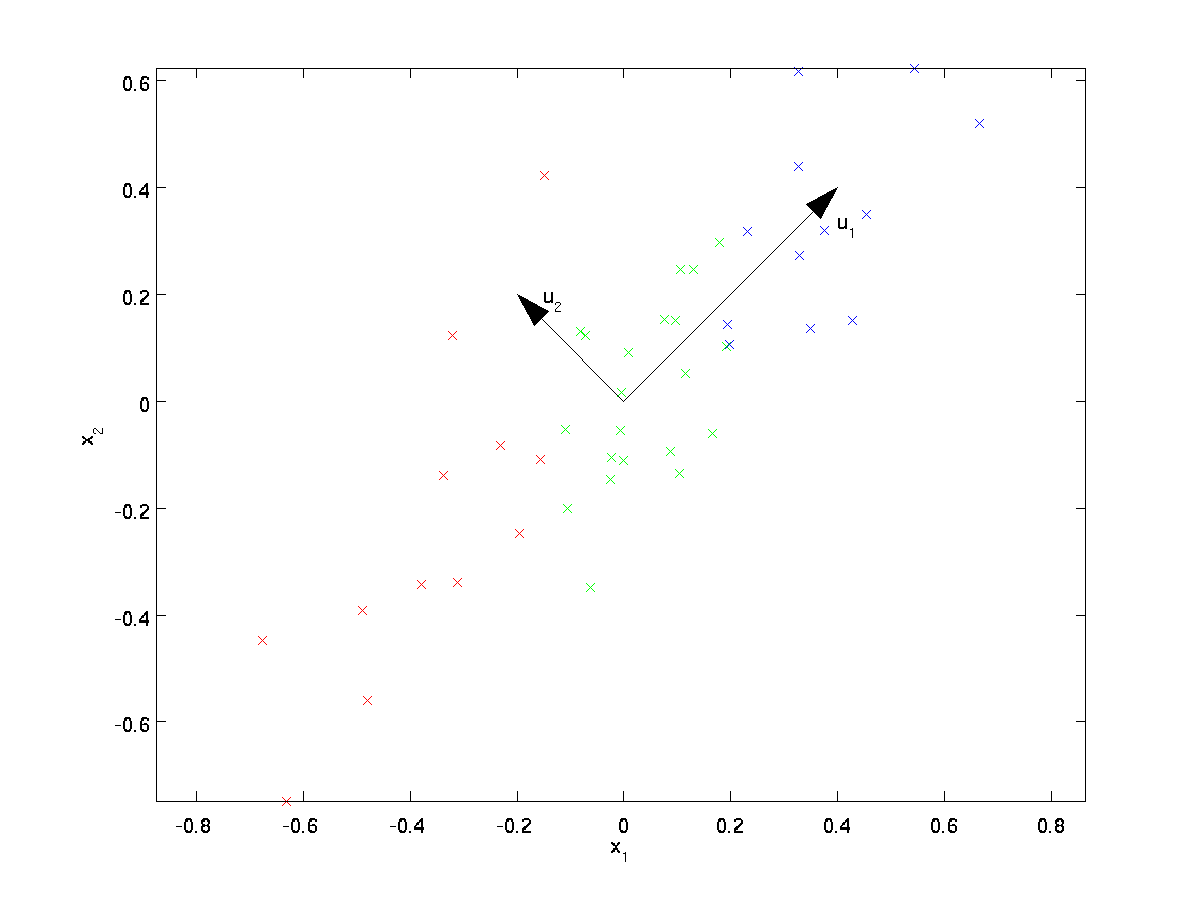
adică, datele variază mult mai mult în direcția \textstyle u_1 decât \textstyle u_2. Pentru a găsi mai formal direcțiile \ textstyle u_1 și \ textstyle u_2, mai întâi calculăm matricea \ textstyle \ Sigma după cum urmează:
\begin{align}\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(I)})(x^{(i)})^T. \end{align}
dacă \textstyle x are zero medie, atunci \textstyle \Sigma este exact matricea de covarianță a \textstyle X. (simbolul „\textstyle \Sigma”, pronunțat „Sigma”, este notația standard pentru denotarea matricei de covarianță. Din păcate, arată la fel ca simbolul însumării, ca în \sum_{i=1}^n i; dar acestea sunt două lucruri diferite.)
se poate arăta apoi că \textstyle u_1—direcția principală de variație a datelor—este Vectorul propriu superior (principal) al \textstyle \Sigma, iar \textstyle u_2 este al doilea vector propriu.
Notă: Dacă sunteți interesat să vedeți o derivare/justificare matematică mai formală a acestui rezultat, consultați notele de curs CS229 (Machine Learning) despre PCA (link-ul din partea de jos a acestei pagini). Cu toate acestea, nu va trebui să faceți acest lucru pentru a urma acest curs.
puteți utiliza software-ul standard de algebră liniară numerică pentru a găsi acești vectori proprii (consultați notele de implementare). Concret, să calculăm vectorii proprii ai \textstyle \ Sigma și să stivăm vectorii proprii în coloane pentru a forma matricea \ textstyle U:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.
vectorii \textstyle u_1 și \textstyle u_2 din exemplul nostru formează o nouă bază în care putem reprezenta datele. Concret, să \textstyle x \ in \ Re^2 fie un exemplu de formare. Atunci \textstyle u_1 ^ Tx este lungimea (magnitudinea) proiecției \textstyle x pe vectorul \textstyle u_1.
în mod similar, \textstyle u_2^Tx este magnitudinea \textstyle x proiectată pe vectorul \textstyle u_2.
rotirea datelor
astfel, putem reprezenta \textstyle x în \textstyle (u_1, u_2)-baza calculând
\begin{align}x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^TX \\ u_2^TX \end{bmatrix} \end{align}
(indicele „rot” provine din observația că aceasta corespunde unei rotații (și, eventual, a unei rotații) reflecția) datelor originale.) Să ia întregul set de formare, și calcula \textstyle x_ {\rm rot}^{(i)} = U^Tx^{(i)} pentru fiecare \textstyle i. trasarea aceste date transformate \ textstyle x_ {\rm rot}, vom obține:

acesta este setul de antrenament rotit în baza \textstyle u_1,\textstyle u_2. În cazul general, \ textstyle U^Tx va fi setul de antrenament rotit în baza \ textstyle u_1, \ textstyle u_2,…, \ textstyle u_n.
una dintre proprietățile \textstyle U este că este o matrice „ortogonală”, ceea ce înseamnă că satisface \textstyle U^TU = UU^T = I. Deci, dacă vreodată trebuie să treceți de la vectorii rotiți \textstyle x_{\rm rot} înapoi la datele originale \textstyle x, puteți calcula
\begin{align}x = U x_{\rm rot}, \end{align}
deoarece \textstyle U x_{\rm rot} = UU^T x = x.
reducând dimensiunea datelor
vedem că direcția principală de variație a datelor este prima dimensiune \textstyle x_{\RM rot, 1} din aceste date rotite. Astfel, dacă dorim să reducem aceste date la o singură dimensiune, putem seta
\begin{align}\tilde{x}^{(i)} = x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} \in \Re.\ end{align}
Mai general, dacă \textstyle x \in \Re^n și dorim să-l reducem la o \textstyle k reprezentare dimensională \textstyle \tilde{X} \in \re^k (unde k< n), am lua primele componente \textstyle k din \textstyle x_{\rm rot}, care corespund direcțiilor de variație top \textstyle K.
Un alt mod de a explica PCA este că \textstyle x_{\rm rot} este un \textstyle N vector dimensional, unde primele câteva componente sunt probabil mari (de ex., în exemplul nostru, am văzut că \ textstyle x_ {\rm rot, 1}^{(i)} = u_1^Tx^{(i)} ia valori rezonabil de mari pentru majoritatea exemplelor \textstyle i), iar componentele ulterioare sunt susceptibile de a fi mici (de exemplu, în exemplul nostru, \textstyle x_{\rm rot,2}^{(i)} = u_2^Tx^{(i)} era mai probabil să fie mici). Ce face PCA scade componentele ulterioare (mai mici) ale \textstyle x_{\rm rot}, și doar le aproximează cu 0. concret, definiția noastră de \textstyle \tilde{x} poate fi, de asemenea, a ajuns la folosind o aproximare a \textstyle x_{\rm rot} în cazul în care toate, dar primele componente \textstyle k sunt zerouri. Cu alte cuvinte, avem:
\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\aprox \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\x_{\rm rot,k+1} \\\ \ vdots \ \x_ {\RM rot,n}\end{bmatrix}= x_ {\RM rot} \end{align}
în exemplul nostru, aceasta ne oferă următoarea diagramă a \textstyle \tilde{X} (folosind \ textstyle n=2, K=1):

cu toate acestea, deoarece componentele finale \textstyle n-k ale \textstyle \tilde{x} așa cum sunt definite mai sus ar fi întotdeauna zero, nu este nevoie să păstrăm aceste zerouri și astfel definim \textstyle \tilde{x} ca un vector \textstyle k-dimensional cu doar primele componente \textstyle k (non-zero).
Acest lucru explică și de ce am vrut să ne exprimăm datele în \textstyle u_1, u_2, \ldots, u_n bază: a decide ce Componente să păstrăm devine doar păstrarea componentelor k \textstyle de top. Când facem acest lucru, spunem, de asemenea, că „reținem componentele top \textstyle k PCA (sau principal).”
recuperarea unei aproximări a datelor
acum, \textstyle \tilde{x} \în \Re^k este o reprezentare „comprimată” de dimensiuni inferioare a originalului \textstyle x \în \Re^n. dat \textstyle \tilde{x}, cum putem recupera o aproximare \textstyle \hat{x} la valoarea inițială a \textstyle x? Dintr-o secțiune anterioară, știm că \textstyle x = U x_{\rm rot}. Mai mult, ne putem gândi la \ textstyle \ tilde{x} ca o aproximare la \ textstyle x_ {\rm rot}, unde am setat ultimele componente \ textstyle n-k la zerouri. Astfel, având în vedere \textstyle \tilde{x} \în \Re^k, îl putem tampona cu \textstyle n-k zerouri pentru a obține aproximarea noastră la \textstyle x_{\rm rot} \în \Re^N. în cele din urmă, pre-înmulțim cu \textstyle U pentru a obține aproximarea noastră la \textstyle x. concret, obținem
\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^K u_i \tilde{x}_i. \end{align}
egalitatea finală de mai sus provine din definiția \ textstyle u dată mai devreme. (Într-o implementare practică, nu am fi de fapt zero pad \textstyle \tilde{x} și apoi înmulțiți cu \textstyle U, deoarece aceasta ar însemna înmulțirea multor lucruri cu zerouri; în schimb, am multiplica doar \textstyle \tilde{x} \în \Re^k cu primele coloane \textstyle k ale \textstyle U ca în expresia finală de mai sus.) Aplicând acest lucru la setul nostru de date, obținem următorul grafic pentru \ textstyle \ hat{x}:
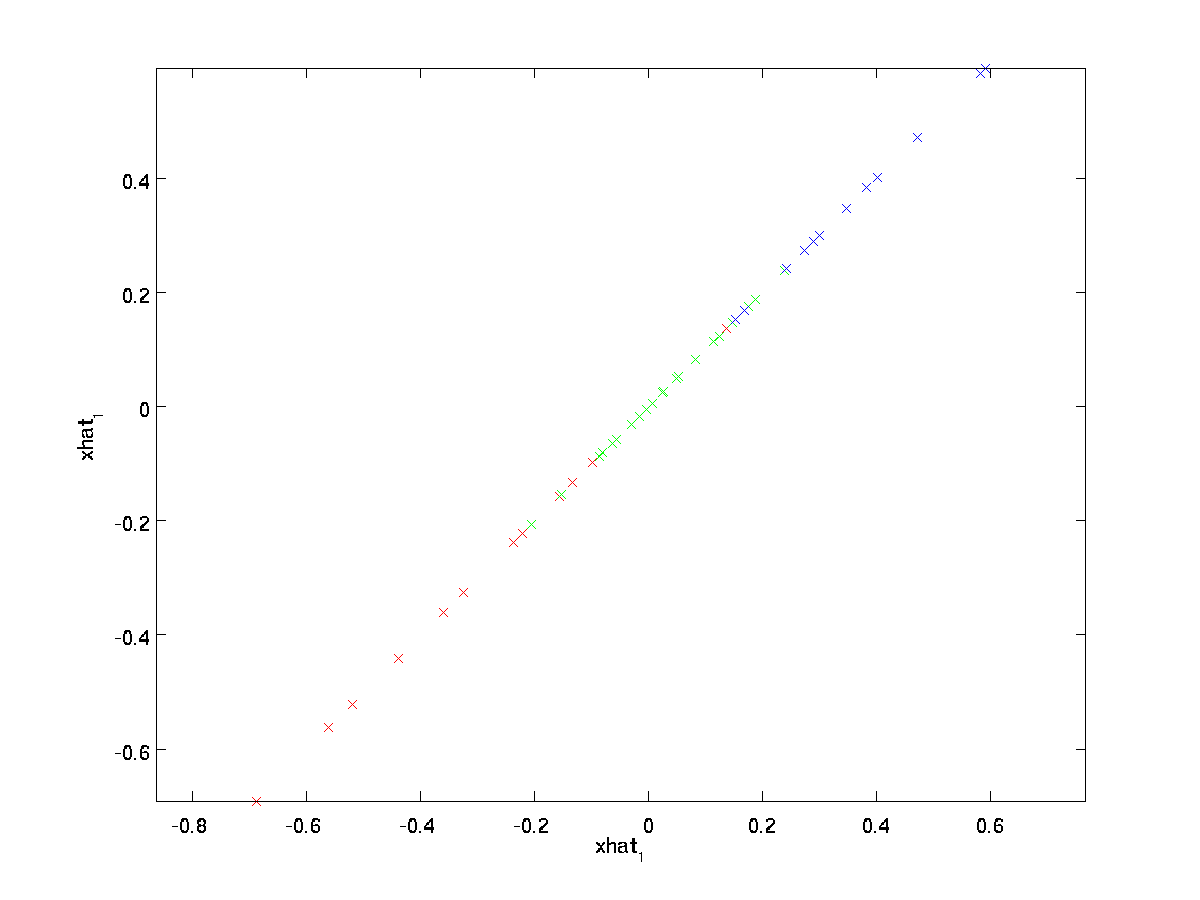
folosim astfel o aproximare dimensională 1 la setul de date original.
dacă antrenați un autoencoder sau un alt algoritm de învățare a caracteristicilor nesupravegheate, timpul de funcționare al algoritmului dvs. va depinde de dimensiunea intrării. Dacă alimentați \textstyle \ tilde{X} \ in \ Re^k în algoritmul dvs. de învățare în loc de \textstyle x, atunci vă veți antrena pe o intrare dimensională inferioară și, astfel, algoritmul dvs. ar putea rula semnificativ mai repede. Pentru multe seturi de date, reprezentarea inferioară dimensională \textstyle \tilde{x} poate fi o aproximare extrem de bună față de original, iar utilizarea PCA în acest fel poate accelera semnificativ algoritmul dvs. în timp ce introduceți foarte puțină eroare de aproximare.
numărul de componente de reținut
cum setăm \textstyle k; adică câte componente PCA ar trebui să reținem? În exemplul nostru simplu 2 dimensional, părea firesc să păstrăm 1 din cele 2 componente, dar pentru datele dimensionale superioare, această decizie este mai puțin banală. Dacă \ textstyle k este prea mare, atunci nu vom comprima prea mult datele; în limita \textstyle k=n, atunci folosim doar datele originale (dar rotite într-o bază diferită). În schimb, dacă \ textstyle k este prea mic, atunci s-ar putea să folosim o aproximare foarte proastă a datelor.
pentru a decide cum să setăm \textstyle k, de obicei ne vom uita la „‘procentajul varianței reținute”‘ pentru diferite valori ale \textstyle k. concret, dacă \textstyle k=n, atunci avem o aproximare exactă a datelor și spunem că 100% din varianță este reținută. Adică., toate variațiile datelor originale sunt păstrate. În schimb, dacă \ textstyle k = 0, atunci aproximăm toate datele cu vectorul zero și astfel 0% din varianță este păstrată.
Mai general, fie \textstyle \ lambda_1, \ lambda_2, \ ldots, \ lambda_n valorile proprii ale \textstyle \ Sigma (sortate în ordine descrescătoare), astfel încât \textstyle \ lambda_j este valoarea proprie corespunzătoare vectorului propriu \ textstyle u_j. apoi, dacă reținem \ textstyle k componente principale, procentul de varianță reținut este dat de:
\începe{align}\frac{\sum_{j=1}^K \lambda_j}{\sum_{j=1}^n \lambda_j}.\ end{align}
în exemplul nostru 2D simplu de mai sus, \textstyle \lambda_1 = 7.29 și \textstyle \lambda_2 = 0.69. Astfel, păstrând doar \textstyle k=1 componente principale, am păstrat \textstyle 7.29/(7.29+0.69) = 0.913, sau 91,3% din varianță.
o definiție mai formală a procentului de varianță reținută depășește domeniul de aplicare al acestor note. Cu toate acestea,este posibil să se arate că \textstyle \lambda_j =\sum_{i=1}^m x_{\rm rot, j}^2. Astfel, dacă \textstyle \ lambda_j \ aprox 0, asta arată că\textstyle x_ {\rm rot, j} este de obicei aproape de 0 oricum și pierdem relativ puțin aproximându-l cu o constantă 0. Acest lucru explică, de asemenea, de ce păstrăm componentele principale de top (corespunzătoare valorilor mai mari ale \textstyle \lambda_j) în loc de cele de jos. Componentele principale de top \textstyle x_ {\rm rot, j} sunt cele care sunt mai variabile și care iau valori mai mari și pentru care am suporta o eroare de aproximare mai mare dacă le-am seta la zero.
în cazul imaginilor, o euristică comună este de a alege \textstyle k astfel încât să păstreze 99% din varianța. Cu alte cuvinte, alegem cea mai mică valoare a \textstyle k care satisface
\begin{align}\frac{\sum_{j=1}^K \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0,99. \ end{align}
în funcție de aplicație, dacă sunteți dispus să suportați o eroare suplimentară, valorile din intervalul 90-98% sunt, de asemenea, uneori utilizate. Când descrieți altora cum ați aplicat PCA, a spune că ați ales \textstyle k pentru a păstra 95% din varianță va fi, de asemenea, o descriere mult mai ușor de interpretat decât a spune că ați păstrat 120 (sau orice alt număr de) componente.
PCA pe imagini
pentru ca PCA să funcționeze, de obicei dorim ca fiecare dintre caracteristicile \textstyle x_1, x_2, \ldots, x_n să aibă o gamă similară de valori cu celelalte (și să aibă o medie apropiată de zero). Dacă ați mai folosit PCA în alte aplicații, este posibil să fi pre-procesat separat fiecare caracteristică pentru a avea varianță medie și unitate zero, estimând separat media și varianța fiecărei caracteristici \ textstyle x_j. cu toate acestea, aceasta nu este pre-procesarea pe care o vom aplica majorității tipurilor de imagini. Mai exact, să presupunem că ne antrenăm algoritmul pe „‘imagini naturale”‘, astfel încât \textstyle x_j este valoarea pixelului \textstyle j. prin „imagini naturale”, ne referim informal la tipul de imagine pe care un animal sau o persoană tipică ar putea să o vadă de-a lungul vieții.
notă: De obicei folosim imagini cu scene în aer liber cu iarbă, copaci etc., și tăiați mici (să zicem 16×16) patch-uri de imagine aleatoriu din acestea pentru a antrena algoritmul. Dar, în practică, majoritatea algoritmilor de învățare a caracteristicilor sunt extrem de robusti pentru tipul exact de imagine pe care este instruit, astfel încât majoritatea imaginilor realizate cu o cameră normală, atât timp cât nu sunt excesiv de neclare sau au artefacte ciudate, ar trebui să funcționeze.
când te antrenezi pe imagini naturale, nu are sens să estimezi o medie și o varianță separate pentru fiecare pixel, deoarece statisticile dintr-o parte a imaginii ar trebui (teoretic) să fie aceleași ca oricare alta.
această proprietate a imaginilor se numește „staționaritate”.”‘
în detaliu, pentru ca PCA să funcționeze bine, Informal solicităm ca (i) caracteristicile să aibă o medie aproximativ zero și (ii) diferitele caracteristici să aibă variații similare între ele. Cu imagini naturale, (ii) este deja satisfăcut chiar și fără normalizarea varianței și, prin urmare, nu vom efectua nicio normalizare a varianței.
(dacă vă antrenați pe date audio—să zicem, pe spectrograme—sau pe date text-să zicem, vectori sac-de—cuvânt-de obicei nu vom efectua nici normalizarea varianței.)
De fapt, PCA este invariant la scalarea datelor, și va returna aceleași vectori proprii, indiferent de scalarea de intrare. Mai formal, dacă înmulțiți fiecare vector de caracteristică \ textstyle x cu un număr pozitiv (scalând astfel fiecare caracteristică din fiecare exemplu de antrenament cu același număr), vectorii proprii de ieșire PCA nu se vor schimba.
deci, nu vom folosi normalizarea varianței. Singura normalizare pe care trebuie să o efectuăm atunci este normalizarea medie, pentru a ne asigura că caracteristicile au o medie în jurul valorii de zero. În funcție de aplicație, foarte des nu ne interesează cât de strălucitoare este imaginea generală de intrare. De exemplu, în activitățile de recunoaștere a obiectelor, luminozitatea generală a imaginii nu afectează obiectele din imagine. Mai formal, nu ne interesează valoarea medie a intensității unui patch de imagine; astfel, putem scădea această valoare, ca formă de normalizare medie.
concret, dacă \textstyle x^{(i)} \în \Re^{n} sunt valorile intensității (în tonuri de gri) ale unui patch de imagine 16×16 (\textstyle n=256), am putea normaliza intensitatea fiecărei imagini \textstyle x^{(i)} după cum urmează:
\mu^{(i)} := \frac{1}{n} \sum_{j=1}^N x^{(i)}_jx^{(i)}_j := x^{(i)}_j – \mu^{(i)}
pentru toate \textstyle j
rețineți că cei doi pași de mai sus se fac separat pentru fiecare imagine \textstyle x^{(i)} și că \textstyle \mu^{(i)} aici este intensitatea medie a imaginii \textstyle x^{(i)}. În special, acest lucru nu este același lucru cu estimarea unei valori medii separat pentru fiecare pixel \textstyle x_j.
dacă vă antrenați algoritmul pe alte imagini decât imaginile naturale (de exemplu, imagini cu caractere scrise de mână sau imagini cu Obiecte izolate unice centrate pe un fundal alb), alte tipuri de normalizare ar putea merita luate în considerare, iar cea mai bună alegere poate fi dependentă de aplicație. Dar atunci când se antrenează pe imagini naturale, utilizarea metodei de normalizare medie pe imagine, așa cum este dată în ecuațiile de mai sus, ar fi o implicită rezonabilă.
albire
am folosit PCA pentru a reduce dimensiunea datelor. Există o etapă de preprocesare strâns legată numită albire (sau, în alte literaturi, sferare) care este necesară pentru unii algoritmi. Dacă ne antrenăm pe imagini, intrarea brută este redundantă, deoarece valorile pixelilor adiacenți sunt foarte corelate. Scopul albirii este de a face intrarea mai puțin redundantă; mai formal, dezideratele noastre sunt că algoritmii noștri de învățare văd o intrare de antrenament în care (i) caracteristicile sunt mai puțin corelate între ele și (ii) caracteristicile au toate aceeași varianță.
exemplu 2D
vom descrie mai întâi albirea folosind exemplul nostru 2D anterior. Vom descrie apoi modul în care acest lucru poate fi combinat cu netezirea și, în final, cum să combinăm acest lucru cu PCA.
cum putem face caracteristicile noastre de intrare necorelate între ele? Am făcut deja acest lucru atunci când calculam \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}.
repetând figura noastră anterioară, graficul nostru pentru \textstyle x_{\rm rot} a fost:

matricea de covarianță a acestor date este dată de:
\begin{align}\begin{bmatrix}7.29 && 0.69\end{bmatrix}.\ end{align}
(notă: Din punct de vedere tehnic, multe dintre afirmațiile din această secțiune despre „covarianță” vor fi adevărate numai dacă datele au o medie zero. În restul acestei secțiuni, vom lua această presupunere ca implicită în declarațiile noastre. Cu toate acestea, chiar dacă Media datelor nu este exact zero, intuițiile pe care le prezentăm aici sunt încă adevărate și, prin urmare, nu ar trebui să vă faceți griji.)
nu este întâmplător faptul că valorile diagonale sunt \textstyle \lambda_1 și \textstyle \lambda_2. Mai mult, intrările off-diagonale sunt zero; astfel, \ textstyle x_ {\rm rot, 1} și \textstyle x_{\rm rot,2} sunt necorelate, satisfăcând una dintre dezideratele noastre pentru date albite (ca caracteristicile să fie mai puțin corelate).
pentru ca fiecare dintre caracteristicile noastre de intrare să aibă varianță unitară, putem redimensiona pur și simplu fiecare caracteristică \textstyle x_{\rm rot,i} prin \textstyle 1/\sqrt{\lambda_i}. În mod concret, definim datele noastre albite \textstyle x_{\rm PCAwhite} \in \Re^n după cum urmează:
\begin{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}}. \ end{align}
trasarea \ textstyle x_ {\rm PCAwhite}, obținem:

aceste date au acum covarianță egală cu matricea de identitate \textstyle I. spunem că \textstyle x_{\rm PCAwhite} este versiunea noastră albită PCA a datelor: diferitele componente ale \textstyle x_{\rm PCAwhite} sunt necorelate și au varianță unitară.
albirea combinată cu reducerea dimensionalității. Dacă doriți să aveți date care sunt albite și care sunt mai puțin dimensionale decât intrarea originală, puteți, de asemenea, să păstrați opțional doar componentele de sus \textstyle k ale \textstyle x_{\rm PCAwhite}. Când combinăm albirea PCA cu regularizarea (descrisă mai târziu), ultimele componente ale \textstyle x_{\rm PCAwhite} vor fi oricum aproape zero și astfel pot fi abandonate în siguranță.
ZCA Whitening
În cele din urmă, se dovedește că acest mod de a obține datele să aibă covarianță identitate \textstyle I nu este unic. Concret, dacă \textstyle R este orice matrice ortogonală, astfel încât să satisfacă \ textstyle RR^T = R^TR = I (mai puțin formal, dacă \textstyle R este o matrice de rotație/reflecție), atunci \textstyle R \,x_{\rm PCAwhite} va avea și covarianță de identitate.
în ZCA whitening, alegem \textstyle R = U. definim
\begin{align}x_{\rm ZCAwhite} = U x_{\rm PCAwhite}\end{align}
plotare \textstyle x_{\rm ZCAwhite}, obținem:

se poate arăta că dintre toate opțiunile posibile pentru \textstyle R, această alegere de rotație face ca \textstyle x_{\RM zcawhite} să fie cât mai aproape posibil de datele de intrare originale \textstyle X.
când folosim ZCA whitening (spre deosebire de PCA Whitening), păstrăm de obicei toate \textstyle n dimensiunile datelor și nu încercăm să le reducem dimensiunea.
Regularizaton
când implementăm albirea PCA sau albirea ZCA în practică, uneori unele dintre valorile proprii \textstyle \lambda_i vor fi aproape numeric de 0 și, prin urmare, etapa de scalare în care împărțim la \sqrt{\lambda_i} ar implica împărțirea la o valoare apropiată de zero; acest lucru poate provoca explozia datelor (ia valori mari) sau altfel să fie instabilă numeric. În practică, prin urmare, implementăm acest pas de scalare folosind o cantitate mică de regularizare și adăugăm o mică constantă \textstyle \ epsilon la valorile proprii înainte de a lua rădăcina pătrată și inversa:
\start{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i + \epsilon}}.\ end{align}
când \ textstyle x ia valori în jurul \ textstyle, o valoare de \textstyle \ epsilon \ aprox 10 ^ {-5} ar putea fi tipică.
pentru cazul imaginilor, adăugarea \textstyle \epsilon aici are și efectul de netezire ușoară (sau filtrare low-pass) a imaginii de intrare. Acest lucru are, de asemenea, un efect de dorit de a elimina artefacte aliasing cauzate de modul în care pixelii sunt prevăzute într-o imagine, și poate îmbunătăți caracteristicile învățate (detalii sunt dincolo de domeniul de aplicare al acestor note).
ZCA whitening este o formă de pre-procesare a datelor care o mapează de la \textstyle x la \textstyle x_{\rm ZCAwhite}. Se pare că acesta este, de asemenea, un model dur al modului în care ochiul biologic (retina) procesează imaginile. Mai exact, pe măsură ce ochiul percepe imagini, majoritatea „pixelilor” adiacenți din ochi vor percepe valori foarte similare, deoarece părțile adiacente ale unei imagini tind să fie foarte corelate în intensitate. Prin urmare, este risipitor pentru ochiul tău să trebuiască să transmită fiecare pixel separat (prin nervul optic) către creier. În schimb, retina dvs. efectuează o operație de decorrelație (aceasta se face prin intermediul neuronilor retinieni care calculează o funcție numită „on center, off surround/off center, on surround”), care este similară cu cea efectuată de ZCA. Acest lucru are ca rezultat o reprezentare mai puțin redundantă a imaginii de intrare, care este apoi transmisă creierului.
implementarea albirii PCA
în această secțiune, rezumăm algoritmii de albire PCA, PCA și ZCA și descriem, de asemenea, modul în care le puteți implementa folosind biblioteci eficiente de algebră liniară.
În primul rând, trebuie să ne asigurăm că datele au (aproximativ) zero-medie. Pentru imaginile naturale, realizăm acest lucru (aproximativ) scăzând valoarea medie a fiecărui patch de imagine.
realizăm acest lucru calculând media pentru fiecare plasture și scăzând-o pentru fiecare plasture. În Matlab, putem face acest lucru folosind
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);apoi, trebuie să calculăm \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(I)})(x^{(i)})^T. Dacă implementați acest lucru în Matlab (sau chiar dacă implementați acest lucru în C++, Java, etc., dar au acces la o bibliotecă eficientă de algebră liniară), făcând-o ca o sumă explicită este ineficientă. În schimb, putem calcula acest lucru într-o singură lovitură ca
sigma = x * x' / size(x, 2);(verificați matematica pentru corectitudine.) Aici, presupunem că x este o structură de date care conține un exemplu de antrenament pe coloană (deci, x este o matrice \textstyle n-by-\textstyle m).
apoi, PCA calculează vectorii proprii ai \Sigma. S-ar putea face acest lucru folosind funcția Matlab eig. Cu toate acestea, deoarece \Sigma este o matrice semi-definită pozitivă simetrică, este mai fiabil din punct de vedere numeric să faceți acest lucru folosind funcția svd. Concret, dacă implementați
= svd(sigma);atunci matricea U va conține vectorii proprii ai \Sigma (un vector propriu pe coloană, sortat în ordine de sus în jos vector propriu), iar intrările diagonale ale matricei S vor conține valorile proprii corespunzătoare (sortate și în ordine descrescătoare). Matricea V va fi egală cu U și poate fi ignorată în siguranță.
(notă: Funcția svd calculează de fapt vectorii singulari și valorile singulare ale unei matrice, care pentru cazul special al unei matrice semi-definite pozitive simetrice—care este tot ceea ce ne preocupă aici—este egală cu vectorii proprii și valorile proprii. O discuție completă a vectorilor singulari vs. vectori proprii este dincolo de sfera acestor note.)
în cele din urmă, puteți calcula \textstyle x_{\rm rot} și \textstyle \tilde{X} după cum urmează:
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keepaceasta oferă reprezentarea PCA a datelor în termeni de \textstyle \tilde{x} \în \Re^k. De altfel, dacă x este o matrice\textstyle n-by- \ textstyle m care conține toate datele dvs. de antrenament, aceasta este o implementare vectorizată, iar expresiile de mai sus funcționează și pentru calculul x_{\rm rot} și \tilde{x} pentru întregul set de antrenament dintr-o singură dată. X_ rezultat {\rm rot} și \ tilde{X} va avea o coloană corespunzătoare fiecărui exemplu de formare.
pentru a calcula datele albite PCA \textstyle x_{\rm PCAwhite}, utilizați
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;deoarece diagonala lui s conține valorile proprii \textstyle \lambda_i, aceasta se dovedește a fi o modalitate compactă de calcul \textstyle x_{\rm PCAwhite,i} = \frac{x_{\RM rot,i} }{\sqrt{\lambda_i}} simultan pentru toate \textstyle I.
în cele din urmă, puteți calcula și datele albite ZCA \textstyle x_{\RM zcawhite} ca:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;