principiul Franck-Condon descrie intensitățile tranzițiilor vibronice sau absorbția sau emisia unui foton. Se afirmă că atunci când o moleculă trece printr-o tranziție electronică, cum ar fi ionizarea, configurația nucleară a moleculei nu are nicio schimbare semnificativă. Acest lucru se datorează faptului că nucleele sunt mult mai masive decât electronii, iar tranziția electronică are loc mai repede decât nucleele pot răspunde. Când nucleul se realiniază cu noua configurație electronică, teoria afirmă că trebuie să sufere o vibrație.
dacă ne imaginăm tranziția verticală de la sol la starea electronică excitată ca apărând dintr-o funcție de undă vibrațională care dă o distribuție de probabilitate a găsirii nucleelor într-o regiune a spațiului,putem determina probabilitatea unui nivel vibrațional dat din integrala de suprapunere \(s_{v’, v}\) care dă suprapunerea funcției de undă vibrațională în sol și starea excitată. Numerele cuantice \(v’\) se referă la starea de bază, iar numerele cuantice \(v\) se referă la starea excitată. Probabilitatea de tranziție poate fi separată în părți electronice și nucleare folosind aproximarea Condon.
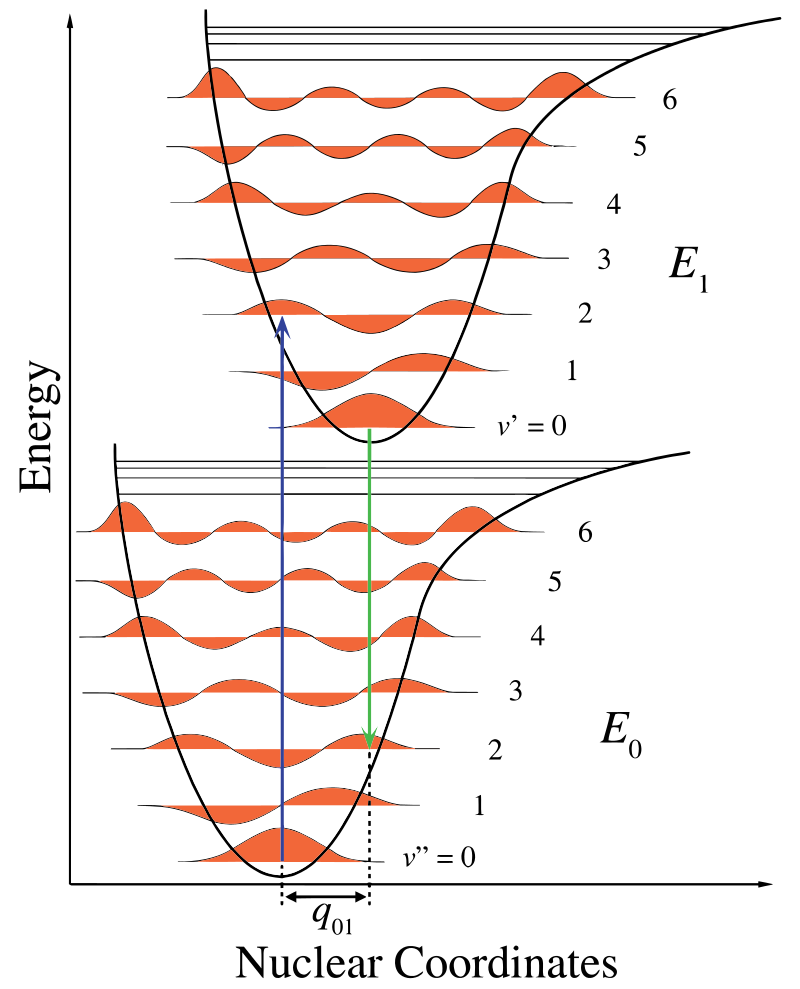
în figura \(\PageIndex{1}\), axa nucleară prezintă o consecință a separării internucleare, iar tranziția vibronică este indicată de săgețile verticale albastre și verzi. Această cifră demonstrează trei lucruri:
- o absorbție duce la o stare de energie mai mare,
- fluorescența duce la o stare de energie mai mică și
- schimbarea coordonatelor nucleare între sol și starea excitată indică o nouă poziție de echilibru pentru potențialul de interacțiune nucleară. Faptul că săgeata de fluorescență este mai scurtă decât absorbția indică faptul că are mai puțină energie sau că lungimea sa de undă este mai lungă.aproximarea clasică a Condonilor este presupunerea că tranziția electronică are loc pe o scară de timp scurtă în comparație cu mișcarea nucleară, astfel încât probabilitatea de tranziție poate fi calculată la o poziție nucleară fixă.
această schimbare a vibrației este menținută în timpul unei stări denumite excitație electronică rapidă. Forțele Coulombice rezultate produc un echilibru așa cum se arată în figură pentru nucleele denumite punct de cotitură. Punctul de cotitură poate fi cartografiat prin trasarea unei linii verticale de la minimul curbei inferioare la intersecția stării electronice superioare. Această procedură este denumită tranziție verticală și a fost discutată anterior în contextul spectroscopiei fotoelectronice (un alt spectroscoy electronic)..
principiul Franck-Condon explică intensitățile relative ale tranzițiilor vibronice prin corelarea probabilității unei tranziții vibraționale cu suprapunerea funcțiilor de undă vibrațională. Se afirmă că probabilitatea unei tranziții vibraționale este ponderată de integrala de suprapunere Franck-Condon:
\
în cadrul aproximării Franck-Condon, nucleele sunt considerate „fixe” în timpul tranzițiilor electronice. Astfel, tranzițiile electronice pot fi considerate tranziții verticale pe curbele electronice de energie potențială (tranziții vierice în figura \(\PageIndex{1}\)).
principiul cuantic Franck-Condon
principiul Franck-Condon are atât o aplicație clasică, cât și cuantică. În mod clasic, principiul Franck-Condon este aproximarea că o tranziție electronică este cel mai probabil să apară fără modificări ale pozițiilor nucleelor din entitatea moleculară și din mediul său. Starea rezultată se numește stare Franck-Condon, iar tranziția implicată, o tranziție verticală. Formularea mecanică cuantică a acestui principiu este că intensitatea unei tranziții vibronice este proporțională cu pătratul integralei de suprapunere dintre funcțiile de undă vibraționale ale celor două stări care sunt implicate în tranziție.
principiul Franck-Condon se bazează pe aproximarea Born-Oppenheimer, care permite separarea funcțiilor de undă electronice \(q\) și nucleare \(Q\) având în vedere funcția de undă totală.
\
deoarece operatorul de tranziție, \(\hat {\mu} (q)\), depinde numai de componenta electronică, componentele nucleare pot fi separate de integrala momentului de tranziție care dictează probabilitatea apariției tranziției:
&= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{suprapunere nucleară}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \Rangle \end{align}\]
dacă integrala de suprapunere nucleară este zero pentru această tranziție, atunci tranziția nu va fi observată, indiferent de magnitudinea factorului electronic.
\(S_{00}\) tranziție evaluată în cadrul modelului oscilatorului armonic
suprapunerea nucleară pentru tranziția zero-zero \(s_{00}\) poate fi calculată destul de simplu folosind definiția formei gaussiene a funcțiilor de undă ale oscilatorului armonic.
funcția de undă cu punct zero în starea electronică a solului este
\
funcția de undă cu punct zero în starea electronică excitată este
\
unde
- \(\alpha = \dfrac{\sqrt{MK}}{\HBAR}\)
- \(r_e\) este lungimea legăturii de echilibru în starea electronică a solului
- \(q_e\) este lungimea legăturii de echilibru în starea electronică excitată
integrala de suprapunere nucleară este
\
exponentul din ecuația \(\ref{FC1}\) poate fi extins ca
\
și folosim
\
și
\
pentru a înlocui și completa pătratul din interiorul integralei. Putem exprima
\.\]
astfel, integrala din ecuația \(\ref{FC2}\) este
\
integrala este o integrală Gaussiană. Puteți arăta că dacă lăsăm \(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\) atunci \(dz = \sqrt{\alpha} dR\) și integrala devine
\
această integrală a fost rezolvată deja, dintr-un tabel de integrale, ecuația \(\ref{FC3}\) devine
\
am urma aceeași procedură pentru a calcula acea suprapunere a vibrației nivelului zero în sol la primul nivel vibrațional excitat al stării excitate: \(s_{01}\).
\(S_{01}\) tranziție evaluată în cadrul modelului oscilatorului armonic
pentru a calcula suprapunerea nivelului de stare zero (\(v=0\)) cu primul nivel de stare excitat (\(v’=1\)) folosim polinomul Hermit \(H_1(x) =2x\) pentru descrierea funcției de undă a stării excitate (a se vedea aici o revizuire a funcțiilor de undă ale oscilatorului armonic). Aici \(x = \ sqrt {\alpha} (R-Q_e)\).
\
cu funcția de undă de punct zero în starea electronică de sol este
\
prima funcție de undă de stare excitată în starea electronică excitată este
\
suprapunerea nivelului de stare de bază zero cu primul nivel de stare excitat (ecuația \(\ref{fc01}\)) este apoi
\
și
\
aceleași substituții pot fi făcute ca mai sus, astfel încât integrala să poată fi scrisă ca (nu este prezentată și să fie demonstrată într-o exerciții pentru teme) și rezultatul final este
\
am putea continua și calcula acea suprapunere a nivelului zero în starea de bază cu toate nivelurile vibraționale ale Luminii Superioare: \(S_{02}\), \(s_{03}\) etc. Fiecare termen corespunde unei tranziții cu o energie diferită, deoarece nivelurile vibraționale au energii diferite. Banda de absorbție are apoi aspectul unei progresii (o progresie Franck-Condon) a tranzițiilor între diferite niveluri, fiecare cu propria probabilitate.
progresii Franck-Condon
pentru a înțelege semnificația formulei de mai sus pentru factorul FC, să examinăm o suprafață de energie potențială de stat la sol și excitat la \(T = 0\) Kelvin. Mai jos sunt prezentate două stări separate de 8.000 cm-1 în energie. Aceasta este separarea energiei între fundul puțurilor lor potențiale, dar și între nivelurile de energie ale punctului zero respectiv. Să presupunem că numărul de undă al modului vibrațional este de 1.000 cm-1 și că lungimea legăturii este crescută datorită faptului că un electron este îndepărtat dintr-un orbital de legătură și plasat într-un orbital anti-legătură la excitația electronică.
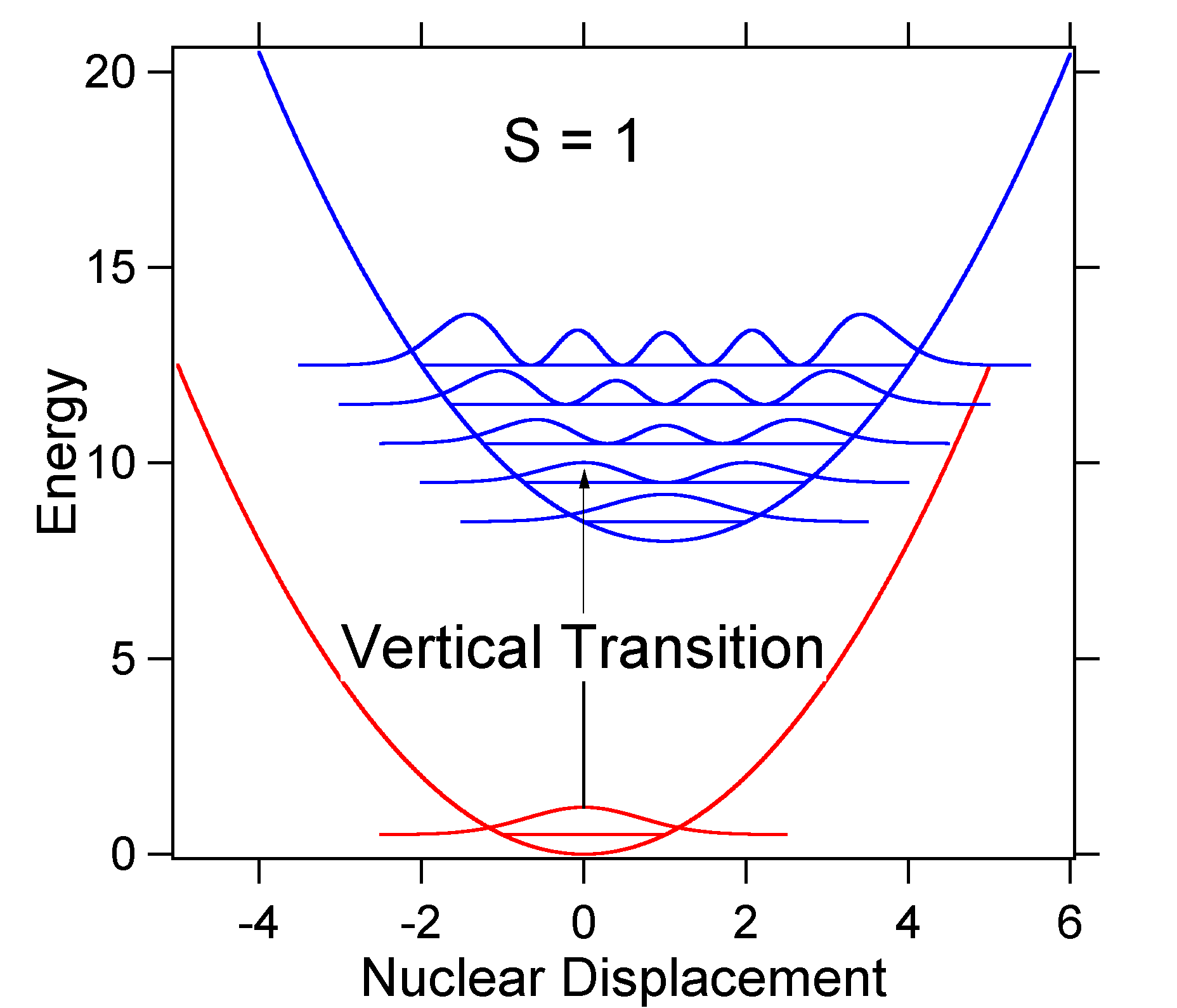
figura \(\PageIndex{2}\): tranzițiile funcțiilor de undă pentru un sistem model oscilator armonic cu deplasare moderată (s=1). conform modelului de mai sus pentru factorul Franck-Condon, am genera un spectru „stick” (Figura \(\PageIndex{3}\)) unde fiecare tranziție vibrațională este infinit de îngustă și tranziția poate avea loc doar atunci când \(E = h\nu\) exact. De exemplu, suprafețele potențiale de energie au fost date pentru S = 1, iar probabilitatea de tranziție la fiecare nivel este dată de bastoane (negru) în figura de mai jos.
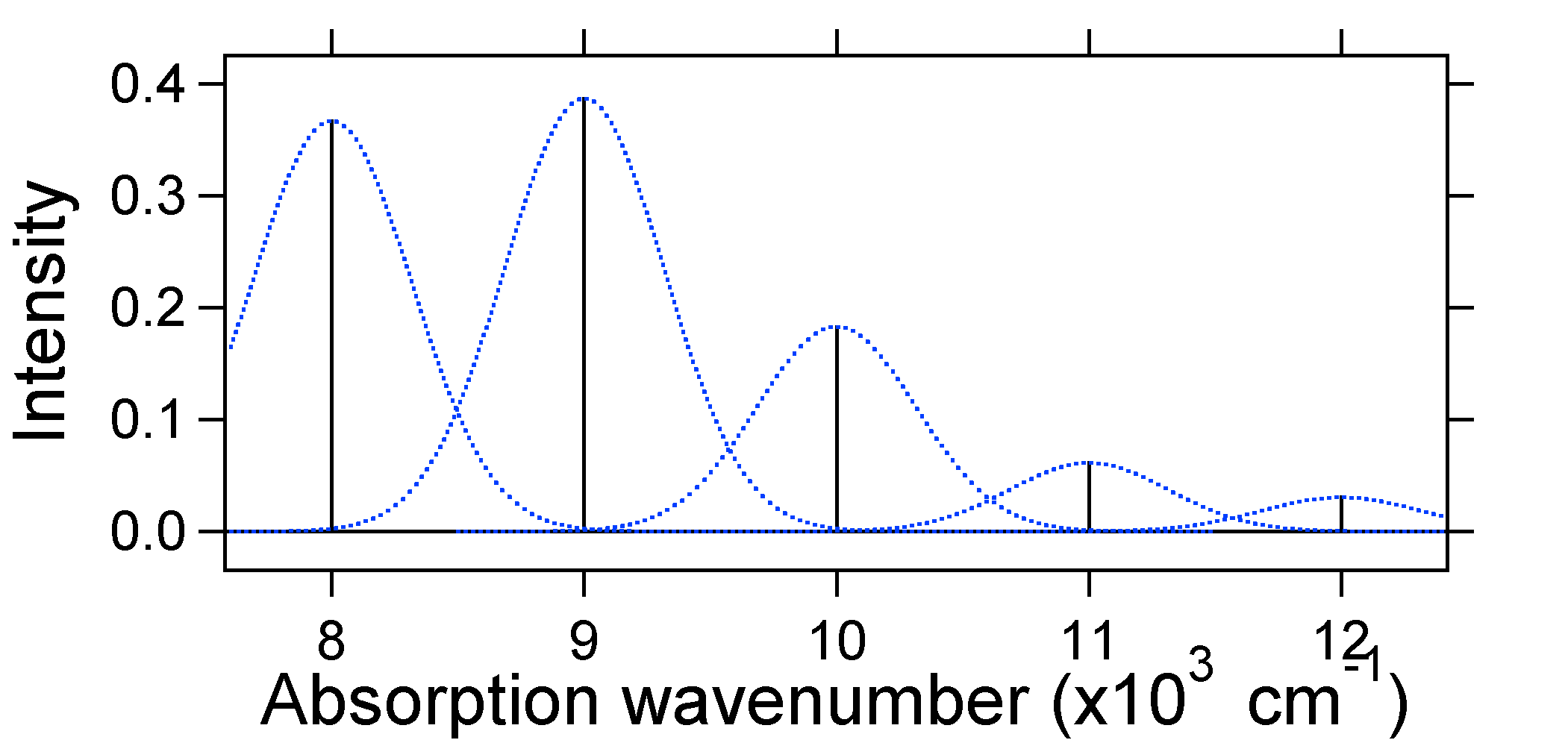
figura \(\PageIndex{3}\): Spectrul Stick, îmbrăcat cu Gaussieni, pentru deplasarea moderată (s=1) sistem oscilator armonic din Figura \(\PageIndex{2}\). Gaussienii punctați care înconjoară fiecare băț oferă o imagine mai realistă a spectrului de absorbție. În primul rând, fiecărui nivel de energie (stick) i se va da o anumită lățime prin faptul că starea are o durată de viață finită. O astfel de lărgire se numește lărgire omogenă, deoarece afectează toate moleculele din ansamblu într-un mod similar. Există, de asemenea, o extindere datorită diferențelor mici în mediul fiecărei molecule. Acest tip de lărgire se numește lărgire neomogenă. Indiferent de origine, modelul de mai sus a fost creat folosind o lărgire Gaussiană
deplasarea nucleară între sol și starea excitată determină forma spectrului de absorbție. Să examinăm atât o deplasare mai mică, cât și o mare stare excitată. În cazul în care \(s = Irak\) și suprafețele potențiale de energie în acest caz sunt:
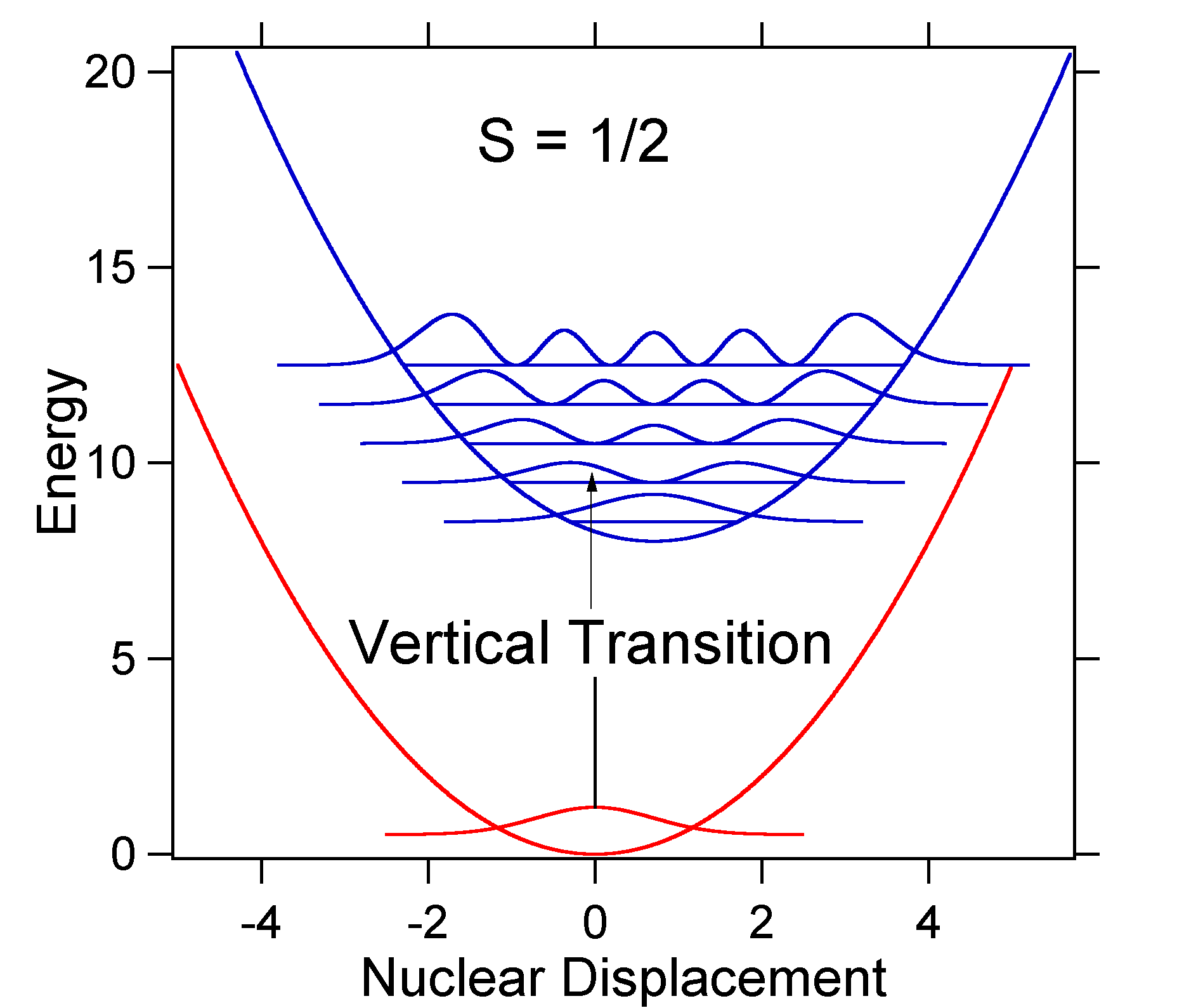
figura \(\PageIndex{4}\): Wavefunctions transitions for a harmonic oscillator model system with small displacement (S=1/2). For this case the „stick” spectrum has the appearance in Figure \(\PageIndex{5}\)
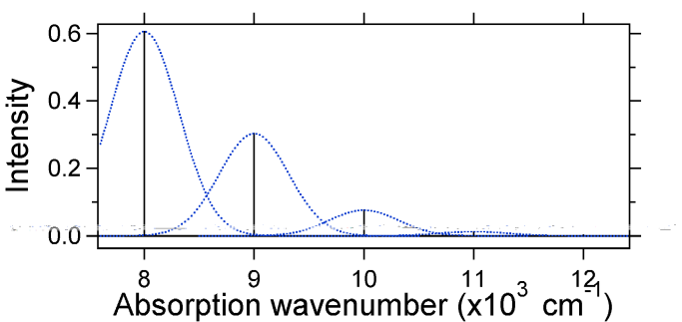
Figure \(\PageIndex{5}\): Stick spectrum, dressed with Gaussians, for the small displacement (S=1/2) harmonic oscillator system from Figure \(\PageIndex{4}\). rețineți că tranziția vibrațională zero-zero sau \(s_{0,0}\) este mult mai mare în cazul în care deplasarea este mică.
ca regulă generală, Constanta \(s\) dă raportul dintre intensitatea tranziției \(v = 2\) și tranziția \(v = 1\). În acest caz, deoarece \(s = 0,5\), tranziția \(v=2\) este 0,5 intensitatea tranziției \(v=1\).
ca exemplu de deplasare mai mare, dispunerea suprafețelor de energie potențială pentru S = 2 este prezentată mai jos.
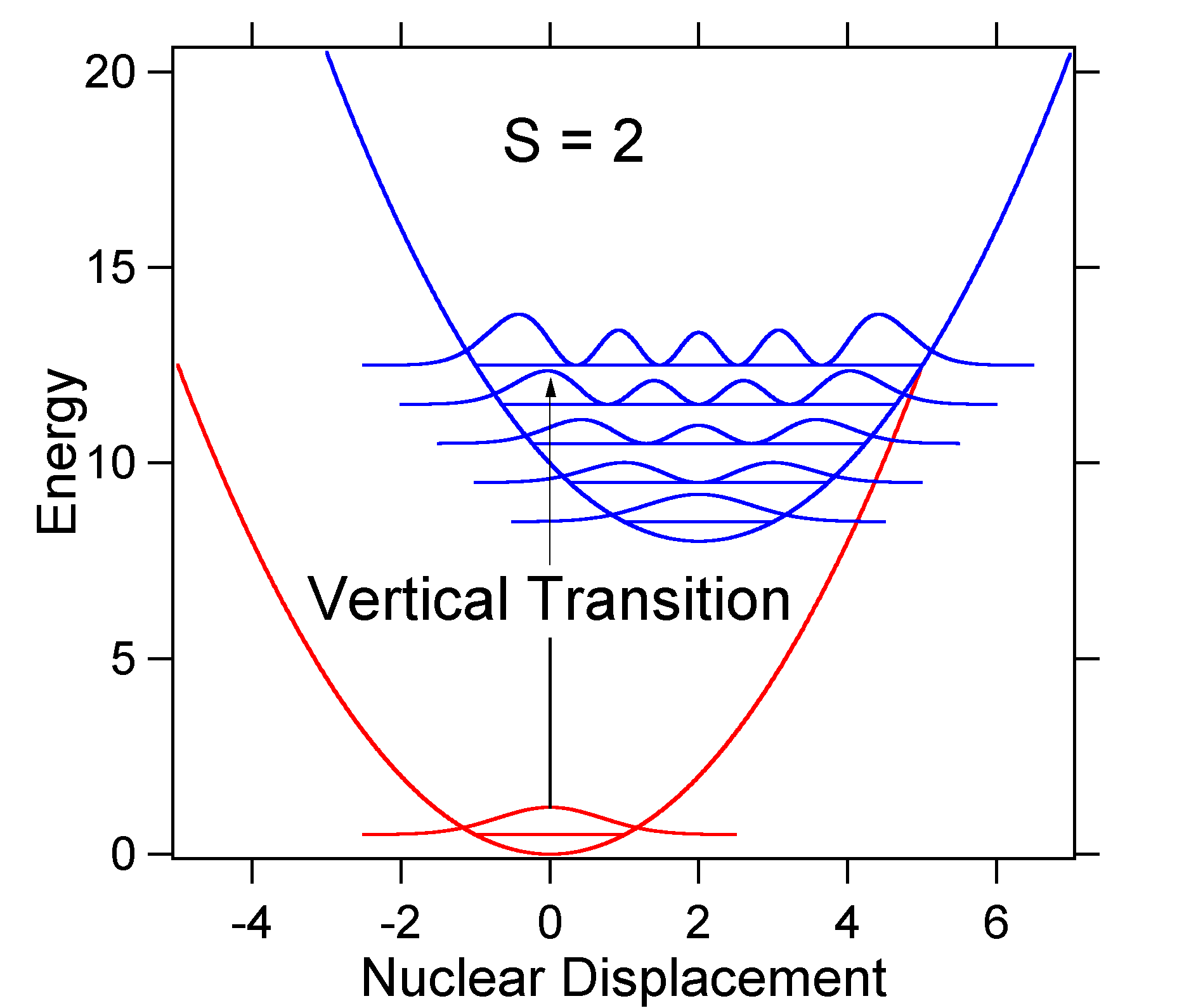
figura \(\PageIndex{6}\): tranziții de funcții de undă pentru un sistem model oscilator armonic cu deplasare puternică (s=2). deplasarea mai mare duce la scăderea suprapunerii nivelului stării de bază cu nivelul v = 0 al stării excitate. Intensitatea maximă va fi atinsă la niveluri vibraționale mai mari, așa cum se arată în spectrul bățului.
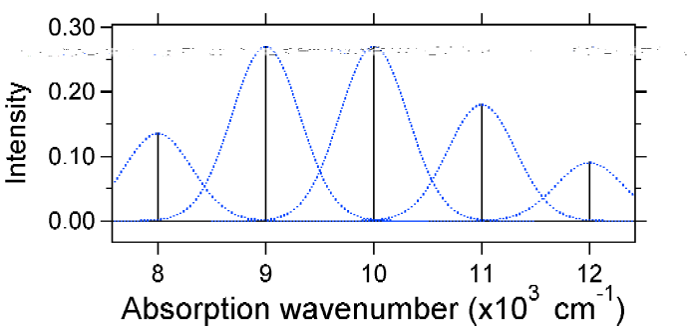
figura \(\PageIndex{7}\): Spectrul Stick, îmbrăcat cu Gaussians, pentru deplasarea Mare (s=2) Sistem oscilator armonic din Figura \(\PageIndex{6}\). spectrele de absorbție reprezentate mai jos au aceeași intensitate integrată, însă formele lor sunt modificate din cauza gradului diferit de deplasare a suprafeței energiei potențiale a stării excitate.
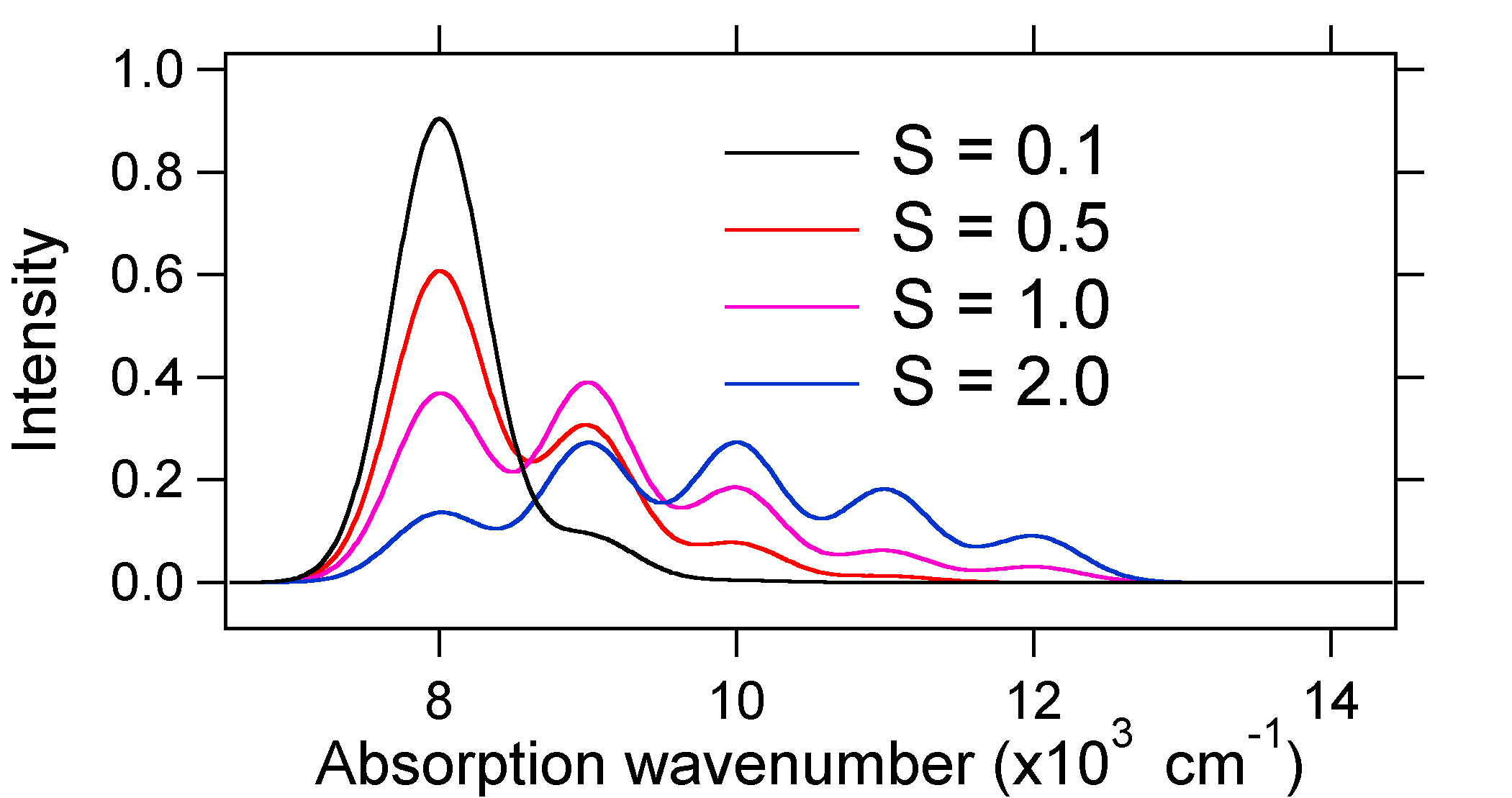
figura \(\PageIndex{8}\): Spectre Stick, îmbrăcate cu Gaussieni, pentru deplasările mici până la mari în sistemul oscilator armonic descris mai sus. deci natura intensităților relative ale benzii vibronice ne poate spune dacă există o deplasare a coordonatei nucleare de echilibru care a însoțit o tranziție. Când va exista o creștere a lungimii legăturii (adică, \(Q_e > R_e\))? Acest lucru se întâmplă atunci când un electron este promovat de la un orbital molecular de legătură la un orbital molecular care nu se leagă sau anti-legătură (adică atunci când ordinea legăturii este mai mică în starea excitată decât starea de bază).
- non-bonding molecular orbital \(\rightarrow\) bonding molecular orbital
- Anti-bonding molecular orbital \(\rightarrow\) bonding molecular orbital
- Anti-bonding molecular orbital \(\rightarrow\) non-bonding molecular orbital
pe scurt, când ordinea legăturii este mai mică în starea excitată decât în starea de bază, atunci \(Q_e > r_e\); o creștere a lungimii legăturii va avea loc atunci când se întâmplă acest lucru.
- J. M. Luis, D. M. Bishop, B. Kirtman. O abordare diferită pentru calcularea factorilor Franck-Condon, inclusiv anarmonicitatea. J. Chem. Fizică., 120 (2004), pp.813-822.
- Atkins, Peter și Julio de Paula. Chimie Fizică pentru științele vieții. 2006. New York, NY: W. H. Freeman și compania. p. 563-564
- principiul Franck-Condon. 1996, 68, 2243. Compendiul IUPAC de terminologie chimică ediția a 2-a (1997). www.iupac.org/goldbook/F02510.pdf
- E. Rabinowitch și Govindjee. Absorbția luminii și soarta excitației energiei. 1969. Principiul Franck-Condon. http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
Contributors
- Matthe Zi Ziering
-
Stefan Franzen (Universitatea de Stat din Carolina de Nord)