ce este un Model ARIMAX?

care este modelul ARIMAX?

dacă ați citit seria noastră de tutoriale de blog pe modele pentru estimarea datelor seriilor de timp, sunteți deja familiarizați cu 3 abordări majore – autoregression, medii mobile și integrare.

care este tema comună în toate aceste modele?

s-au bazat exclusiv pe o singură variabilă.

cu toate acestea, un model poate lua în considerare și mai mult decât prețurile trecute sau reziduurile anterioare.

și acestea sunt așa-numitele modele „MAX”, ARMAX fiind versiunea neintegrată și arimax-echivalentul său integrat.

Deci, în acest tutorial, vom explora cum arată și vă vom arăta cum să le implementați în Python pas cu pas.

Să începem,da?

de ce sunt Armax și ARIMAX numite modele „MAX”?

numele ARMAX și ARIMAX vin ca extensii ale ARMA și respectiv ARIMA. X-ul adăugat la capăt înseamnă „exogen”. Cu alte cuvinte, sugerează adăugarea unei variabile exterioare diferite separate pentru a ajuta la măsurarea variabilei noastre endogene.

ecuația modelului ARMAX și ARIMAX:

deoarece singura diferență dintre ARMAX și ARIMAX este că unul este integrat și celălalt nu, putem examina unul dintre ele și apoi să evidențiem modul în care celălalt ar diferi.

am explorat un model integrat în ultimul nostru articol de blog (Arima), așa că să vedem cum arată ecuația ARIMAX.

ΔPt =c+ßX+ϕ1 ΔPt-1 + θ1 ϵt-1+ϵt

desigur, ecuația pentru ARMAX ar fi la fel, doar ne-ar folosi variabilă reală, spune P, în loc de delta.

Pt=c+XX+XX1 Pt-1+ XX1 XXT-1 +XXT

descompunerea ecuației ARIMAX:

ne putem gândi la ARMAX ca la un caz special al arimax, unde ordinea integrării este 0.

deci, pentru restul tutorialului, ne vom concentra pe ARIMAX.

și vom începe prin descompunerea diferitelor părți din ea. Pentru început, Pt și Pt-1 reprezintă valorile din perioada curentă și respectiv 1 Perioadă în urmă.

în mod similar, pentru aceleași două perioade, sunt folosiți termenii de eroare pentru următoarele două perioade. Și, desigur, c este doar un factor constant de bază.

cei doi parametri, și anume, și anume, și anume, și anume, ce părți din valoarea Pt-1 și eroarea din ultima perioadă, și anume, sunt relevante pentru estimarea celei curente.

acum, cele două noi adăugiri la model sunt „X” și coeficientul său de la zero. La fel ca si in cazul modelului, acesta este un coeficient care va fi estimat pe baza selectiei modelului si a datelor. Dar cum rămâne cu X?

ce este o variabilă exogenă?

Ei bine, X este variabila exogenă și poate fi orice variabilă care ne interesează.

poate fi o măsurare care variază în timp, cum ar fi rata inflației sau prețul unui indice diferit. Sau o variabilă categorică care separă diferitele zile ale săptămânii. Poate fi, de asemenea, o contabilitate booleană pentru perioadele festive speciale. În cele din urmă, poate reprezenta o combinație de mai mulți factori externi diferiți.

ideea este că poate fi orice altă variabilă sau variabile care pot afecta prețurile, atâta timp cât avem datele disponibile.

astfel de factori externi sunt cunoscuți ca variabile exogene în regresia noastră. Folosim valorile lor pentru a prezice și explica cea care ne interesează, care se întâmplă să fie prețurile curente în cazul nostru.

cum se implementează modelele ARMAX și Arimax în Python?

destul de convenabil, pachetul statsmodels vine cu o metodă numită ARIMA, care este pe deplin capabilă să gestioneze astfel de intrări suplimentare.

începem prin specificarea caracteristicilor modelului și a ordinelor modelului:

după ce am făcut asta, trebuie să specificăm și argumentul exogen numit „exog”.

valoarea pe care vrem să o transmitem trebuie să fie o matrice de un fel, deoarece dorim să avem valori asociate cu fiecare perioadă de timp.

de exemplu, putem folosi prețurile S&p ca această variabilă exogenă, deoarece le avem deja în datele noastre.

acum, suntem gata pentru a se potrivi un model ARIMAX (1,1,1).

asigurați-vă că denumiți variabila de model într-un mod care o deosebește de modele similare. În acest caz, alegem să facem acest lucru adăugând „X, spx” la sfârșit pentru a indica faptul că variabila exogenă este S&P.

apoi, după cum se poate observa din fragmente, setăm acest lucru egal cu metoda ARIMA ca înainte, adăugăm seriile de timp și ordinea, așa cum suntem obișnuiți. În cele din urmă, între cele două, setăm argumentul „exog” egal cu „DF SPX”, care indică prețurile s&p.

dacă potrivim acest model și tipărim tabelul sumar, vom vedea că obținem un rând suplimentar pentru prețurile S&p.

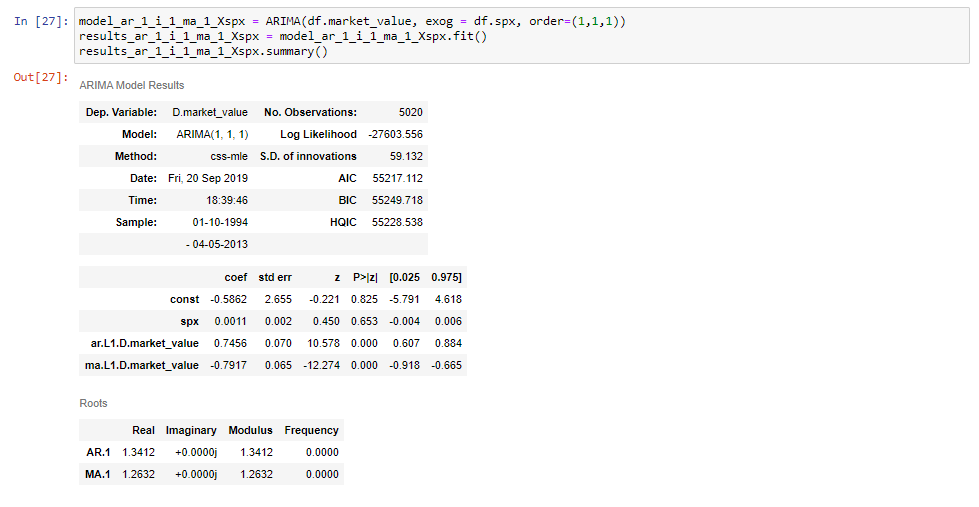
și asta e tot ce este de făcut!

am văzut cu succes cum să implementăm un model Arimax în Python.

Dacă doriți să aflați mai multe despre arimax și alte modele de serii de timp în Python, asigurați-vă că consultați tutorialele Python pas cu pas. Dacă sunteți nou în Python și sunteți entuziasmat să aflați mai multe, acest articol cuprinzător despre învățarea programării Python vă va ghida până la instalare, prin IDE-uri Python, Biblioteci și cadre, până la cele mai bune căi de carieră Python și perspective de locuri de muncă.

sunteți gata să faceți următorul pas către o carieră în știința datelor?

consultați programul complet de știință a datelor astăzi. Începeți cu fundamentele cu cursurile noastre de statistici, matematică și Excel. Construiți o experiență pas cu pas cu SQL, Python, R, Power BI și Tableau. Și îmbunătățiți-vă abilitățile cu învățarea automată, învățarea profundă, modelarea riscului de Credit, analiza seriilor de timp și Analiza clienților în Python. Încă nu sunteți sigur că doriți să vă transformați interesul pentru știința datelor într-o carieră? Puteți explora curriculum-ul sau vă puteți înscrie gratuit pentru 15 ore de conținut video începător la avansat, făcând clic pe butonul de mai jos.