
o rețea neuronală artificială (Ann) este formată din mulți neuroni interconectați:
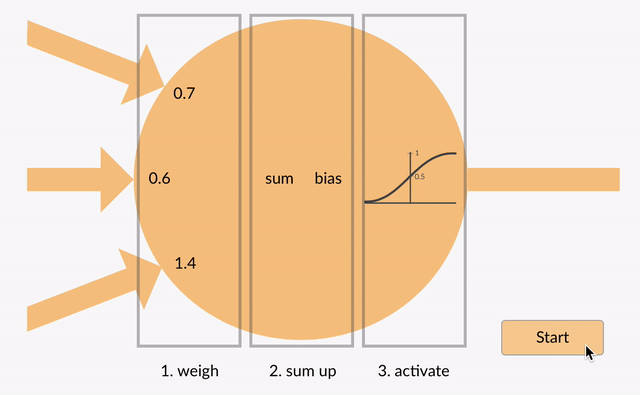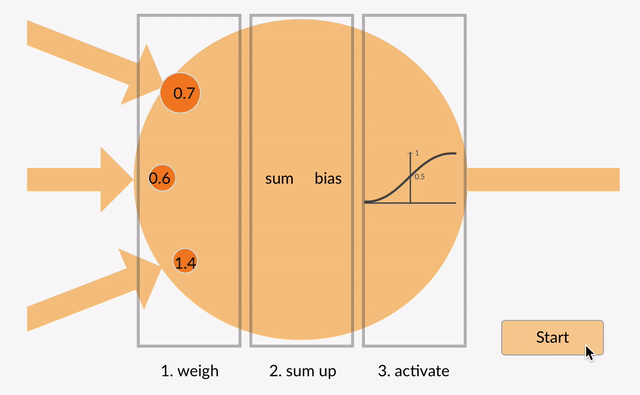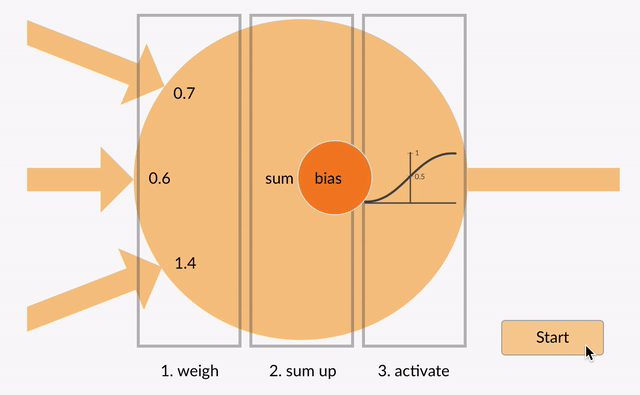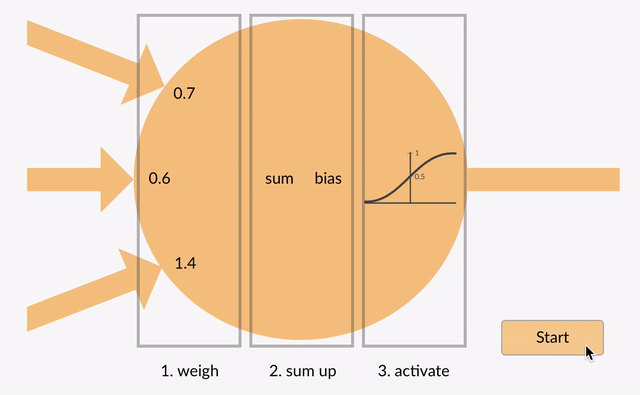
fiecare neuron ia în unele numere în virgulă mobilă (de exemplu, 1.0, 0.5, -1.0) și le înmulțește cu alte numere în virgulă mobilă (de exemplu, 0,7, 0,6, 1,4) cunoscute sub numele de greutăți (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Greutățile acționează ca un mecanism de concentrare sau ignorare a anumitor intrări.

greutățile acționează ca porți moi pentru a ignora unele caracteristici (0) și concentrați-vă pe alții (+1) sau chiar inhibați-i (-1)
intrările ponderate se însumează împreună (de ex. 0.7 + 0.3 + -1.4 = -0.4) împreună cu o valoare de părtinire (de exemplu, -0.4 + -0.1 = -0.5).
valoarea însumată (x) este acum transformată într-o valoare de ieșire (y) în funcție de funcția de activare a neuronului (y = f(x)). Unele funcții de activare populare sunt prezentate mai jos:

de ex.-0.5 dacă folosim funcția de activare a unității liniare rectificate scurgeri (Relu scurgeri): y = f(x) = f(-0,5) = max(0,1*-0,5, -0,5) = max(-0,05, -0,5) = -0.05
valoarea de ieșire a neuronului (de exemplu -0,05) este adesea o intrare pentru un alt neuron.
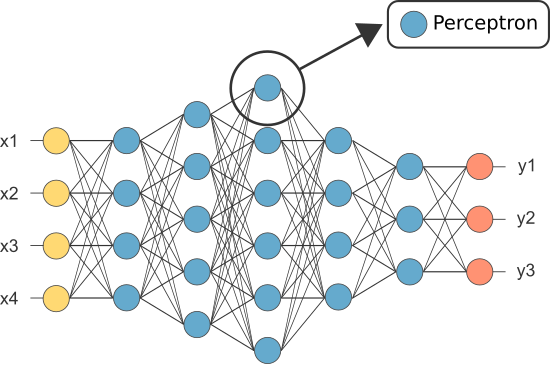
cu toate acestea, unul dintre primii ANS a fost cunoscut sub numele de perceptron și a constat un singur neuron.

ieșirea (singurului) neuron al perceptronului acționează ca predicție finală.

permite codul nostru percepton:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(notă: nu am inclus niciun algoritm de învățare în exemplul nostru de mai sus — vom acoperi algoritmii de învățare într-un alt tutorial)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

deci, de ce avem nevoie de atât de mulți neuroni într-un ANN dacă cineva va fi suficient (ca clasificator)?

Din păcate, neuronii individuali sunt capabili să clasifice date separabile liniar.

cu toate acestea, prin combinarea neuronilor împreună, combinăm în esență limitele lor de decizie. Prin urmare, un ANN compus din mulți neuroni este capabil să învețe limite de decizie complexe, neliniare.

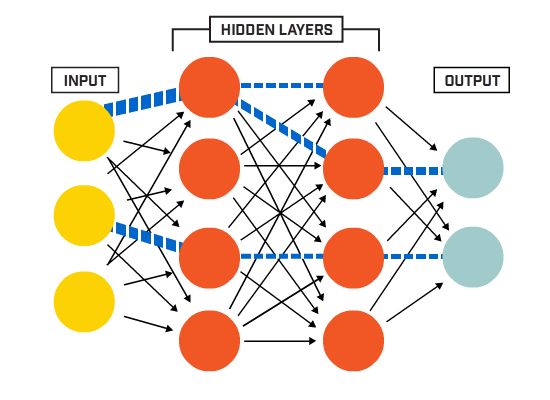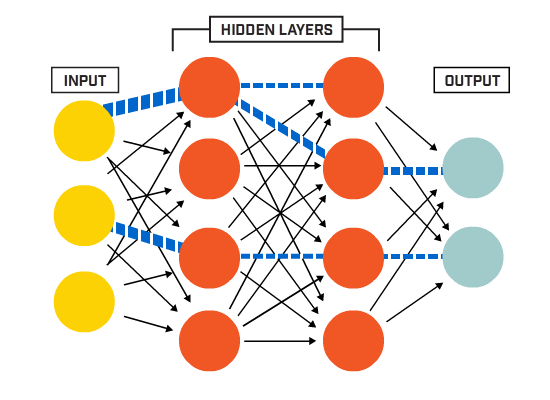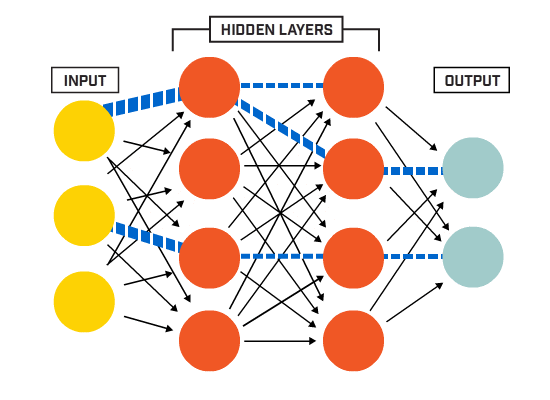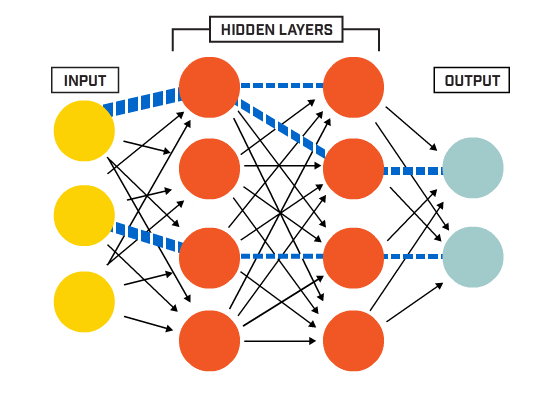
neuronii sunt conectați împreună conform unei arhitecturi de rețea specifice. Deși există arhitecturi diferite, aproape toate conțin straturi. (NB: Neuronii din același strat nu se conectează între ei)
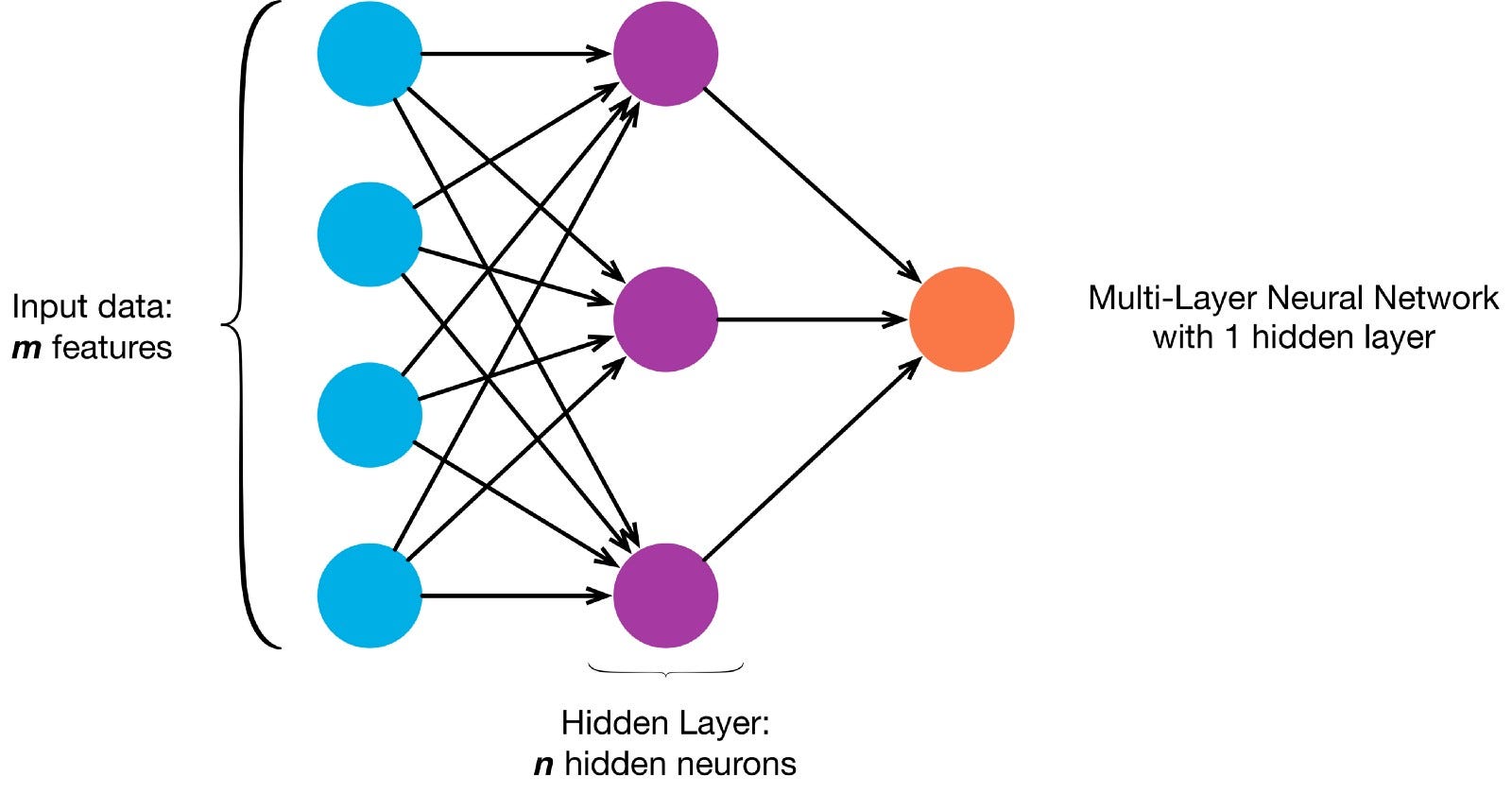
există de obicei un strat de intrare (care conține un număr de neuroni egal cu numărul de caracteristici de intrare din date), un strat de ieșire (care conține un număr de neuroni egal cu numărul de clase) și un strat ascuns (care conține orice număr de neuroni).

pot exista mai multe straturi ascunse pentru a permite rețelei neuronale să învețe limite de decizie mai complexe net cu mai mult de un strat ascuns este considerat o rețea neuronală profundă).
să construim un NN profund pentru a picta această imagine:

permite descărcarea imaginea și încărcarea pixelilor într-o matrice
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
acum predarea Ann-ului nostru pentru a picta este o sarcină de învățare supravegheată, deci trebuie să creăm un set de instruire etichetat (datele noastre de instruire vor avea intrări și etichete de ieșire așteptate pentru fiecare intrare). Intrările de antrenament vor avea 2 valori (coordonatele x,y ale fiecărui pixel).
având în vedere simplitatea imaginii, am putea aborda de fapt această problemă într-unul din cele două moduri. O problemă de clasificare (în cazul în care net neuronale prezice dacă un pixel aparține clasei „albastru” sau clasa „gri”, având în vedere coordonatele sale xy) sau o problemă de regresie (în cazul în care net neuronale prezice valori RGB pentru un pixel dat coordonatele sale).
dacă tratăm acest lucru ca pe o problemă de regresie: rezultatele antrenamentului vor avea 3 valori (valorile R,g,b normalizate pentru fiecare pixel). – Să folosim această metodă pentru moment.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
acum vă permite să creați ANN nostru:

- ar trebui să aibă 2 neuroni în stratul de intrare (deoarece există 2 valori de luat: x & Y coordonate).
- ar trebui să aibă 3 neuroni în stratul de ieșire (deoarece există 3 valori de învățat: r, g, b).
- numărul de straturi ascunse și numărul de neuroni din fiecare strat ascuns sunt doi hiperparametri cu care să experimentăm (precum și numărul de epoci pentru care îl vom antrena, funcția de activare etc.) — voi folosi 10 straturi ascunse cu 100 de neuroni în fiecare strat ascuns (făcând din aceasta o rețea neuronală profundă)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
rețeaua instruită poate prezice acum valorile RGB normalizate pentru orice coordonate (x, y = 1,1).
ann.predict(])
array (])
permite utilizarea ANN pentru a prezice valorile rgb pentru fiecare coordonată și permite afișarea valorilor RGB prezise pentru întreaga imagine pentru a vedea cât de bine a făcut — o (calitativ-vom lăsa valori de evaluare pentru un alt tutorial)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

încercați să schimbați hiperparametrii pentru a obține rezultate mai bune.
dacă în loc să tratăm acest lucru ca pe o problemă de regresie, îl tratăm ca pe o problemă de clasificare, atunci ieșirile de antrenament vor avea 2 valori (probabilitățile pixelului aparținând fiecăreia dintre cele două clase: „albastru” și „gri”)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
putem reconstrui ANN-ul nostru ca clasificator binar cu 2 neuroni în stratul de intrare, 2 neuroni în stratul de ieșire și 100 de neuroni în stratul ascuns (cu 10 straturi ascunse)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
acum putem folosi an instruit pentru a prezice clasa de care aparține fiecare pixel (0: „gri” sau 1: „Albastru”). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: „grey”)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

