Introducere în estimarea mișcării cu flux optic

în acest tutorial, ne scufundăm în fundamentele fluxului optic, ne uităm la unele dintre aplicațiile sale și implementăm cele două variante principale (rare și dense). De asemenea, discutăm pe scurt abordări mai recente folosind învățarea profundă și direcții viitoare promițătoare.

descoperirile recente în cercetarea viziunii computerizate au permis mașinilor să perceapă lumea înconjurătoare prin tehnici precum detectarea obiectelor pentru detectarea instanțelor obiectelor aparținând unei anumite clase și segmentarea semantică pentru clasificarea pixelilor.

cu toate acestea, pentru procesarea intrărilor video în timp real, majoritatea implementărilor acestor tehnici abordează doar relațiile obiectelor din același cadru \((x, y)\) ignorând informațiile despre timp \((t)\). Cu alte cuvinte, ele reevaluează fiecare cadru independent, ca și cum ar fi imagini complet independente, pentru fiecare rulare. Cu toate acestea, ce se întâmplă dacă avem nevoie de relațiile dintre cadrele consecutive, de exemplu, dorim să urmărim mișcarea vehiculelor pe cadre pentru a estima viteza actuală și a prezice poziția sa în cadrul următor?

sau, alternativ, ce se întâmplă dacă avem nevoie de informații despre relațiile umane între cadrele consecutive pentru a recunoaște acțiunile umane, cum ar fi tir cu arcul, baseball-ul și baschetul?

în acest tutorial, vom afla ce este fluxul optic, cum să implementăm cele două variante principale (rare și dense) și, de asemenea, să obținem o imagine de ansamblu a abordărilor mai recente care implică învățarea profundă și direcțiile viitoare promițătoare.

Ce este fluxul optic?
implementarea fluxului optic rar
implementarea fluxului optic dens
învățarea profundă și dincolo

ce este fluxul optic?

să începem cu o înțelegere la nivel înalt a fluxului optic. Fluxul optic este mișcarea obiectelor între cadre consecutive de secvență, cauzată de mișcarea relativă dintre obiect și cameră. Problema fluxului optic poate fi exprimată ca:

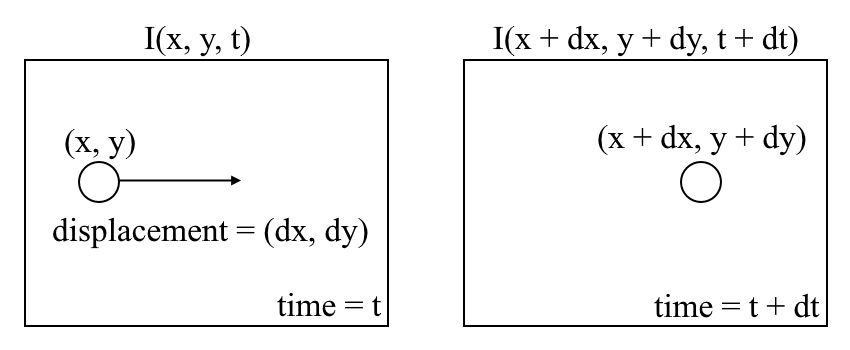
unde între cadre consecutive, putem exprima intensitatea imaginii \((I)\) în funcție de spațiu \((x, y)\) și timpul \((T)\). Cu alte cuvinte, dacă luăm prima imagine \(I(X, y, t)\) și îi mutăm pixelii cu \((dx, dy)\) peste \(t\) timp, obținem noua imagine \(I(x + dx, y + dy, t + dt)\).în primul rând, presupunem că intensitățile pixelilor unui obiect sunt constante între cadre consecutive.

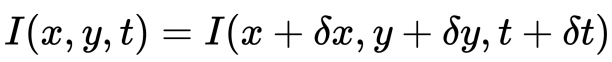
În al doilea rând, luăm aproximarea seriei Taylor a RHS și eliminăm termenii comuni.

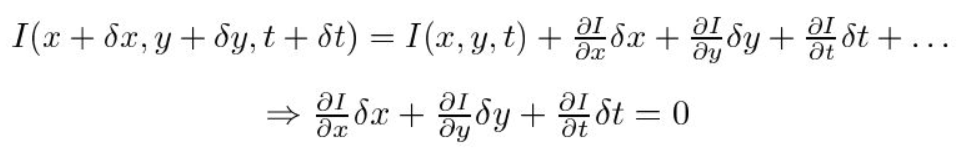
În al treilea rând, împărțim la \(dt\) pentru a obține ecuația fluxului optic:

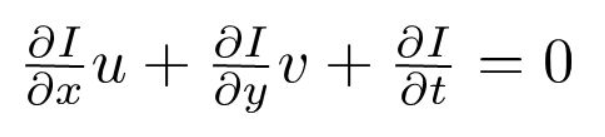
unde \(u = dx/dt\) și \(v = dy / dt\).

\(dI/dx, dI/dy\) și \(dI / dt\) sunt gradienții de imagine de-a lungul axei orizontale, axei verticale și timpului. Prin urmare, încheiem cu problema fluxului optic, adică rezolvarea \(u (DX/dt)\) și \(v (dy/dt)\) pentru a determina mișcarea în timp. Este posibil să observați că nu putem rezolva direct ecuația fluxului optic pentru \(u\) și \(v\) deoarece există o singură ecuație pentru două variabile necunoscute. Vom implementa câteva metode, cum ar fi metoda Lucas-Kanade, pentru a aborda această problemă.

fluxul optic rar vs dens

fluxul optic rar oferă vectorii de flux ai unor „caracteristici interesante” (să zicem câțiva pixeli care descriu marginile sau colțurile unui obiect) în cadru, în timp ce fluxul optic dens, care oferă vectorii de flux ai întregului cadru (toți pixelii) – până la un vector de flux pe pixel. După cum ați fi ghicit, fluxul optic dens are o precizie mai mare, cu prețul de a fi lent/scump din punct de vedere al calculului.

implementarea fluxului optic rar

fluxul optic rar selectează un set de caracteristici rare de pixeli (de exemplu, caracteristici interesante, cum ar fi marginile și colțurile) pentru a urmări vectorii de viteză (mișcare). Caracteristicile extrase sunt transmise în funcția de flux optic de la cadru la cadru pentru a se asigura că aceleași puncte sunt urmărite. Există diverse implementări ale fluxului optic rar, inclusiv metoda Lucas-Kanade, metoda Horn–Schunck, metoda Buxton-Buxton și multe altele. Vom folosi metoda Lucas-Kanade cu OpenCV, o bibliotecă open source de algoritmi de viziune computerizată, pentru implementare.

configurarea mediului dvs.

dacă nu aveți deja OpenCV instalat, deschideți terminalul și rulați:

pip install opencv-python

acum, clonați depozitul tutorial rulând:

git clone https://github.com/chuanenlin/optical-flow.git

în continuare, deschideți sparse-starter.py cu editorul de text. Vom scrie tot codul în acest fișier Python.

Configurarea OpenCV pentru a citi un videoclip și configurarea parametrilor

Detector de colț Shi-Tomasi – selectarea pixelilor de urmărit

pentru implementarea fluxului optic rar, urmărim doar mișcarea unui set de caracteristici de pixeli. Caracteristicile din imagini sunt puncte de interes care prezintă informații bogate despre conținutul imaginii. De exemplu, astfel de caracteristici pot fi puncte din imagine care sunt invariante la modificările de traducere, scară, rotație și intensitate, cum ar fi colțurile.

detectorul de colț Shi-Tomasi este foarte asemănător cu popularul detector de colț Harris, care poate fi implementat prin următoarele trei proceduri:

1. determinați ferestrele (patch-uri mici de imagine) cu gradienți mari (variații ale intensității imaginii) atunci când sunt traduse în ambele direcții \(x\) și \(y\).
2. pentru fiecare fereastră, calcula un scor \(R\).
3. în funcție de valoarea \(R\), fiecare fereastră este clasificată ca un plat, margine sau colț.

dacă doriți să aflați mai multe despre o explicație matematică pas cu pas a detectorului Harris Corner, nu ezitați să parcurgeți aceste diapozitive.

Shi și Tomasi au făcut mai târziu o modificare mică, dar eficientă, a detectorului Harris Corner în hârtia lor caracteristici bune de urmărit.

modificarea este la ecuația în care se calculează scorul \(R\). În detectorul Harris Corner, funcția de notare este dată de:

$$
\begin{array}{c}{r=\operatorname{det} M-k(\operatorname{trace} M)^{2}}\newline \
{\operatorname{det} M=\lambda_{1} \lambda_{2}\newline \
{\operatorname{trace} m=\lambda_{1}+\lambda_{2}\end{array}
$$

în schimb, shi-Tomasi a propus funcția de notare ca:

$$
r=\min \left(\lambda_{1}, \lambda_{2}\Right)
$$

ceea ce înseamnă practic că dacă \(R\) este mai mare decât un prag, este clasificat ca un colț. Următoarele compară funcțiile de notare ale lui Harris (stânga) și Shi-Tomasi(dreapta) în spațiul \(inktif1-inktif2\).

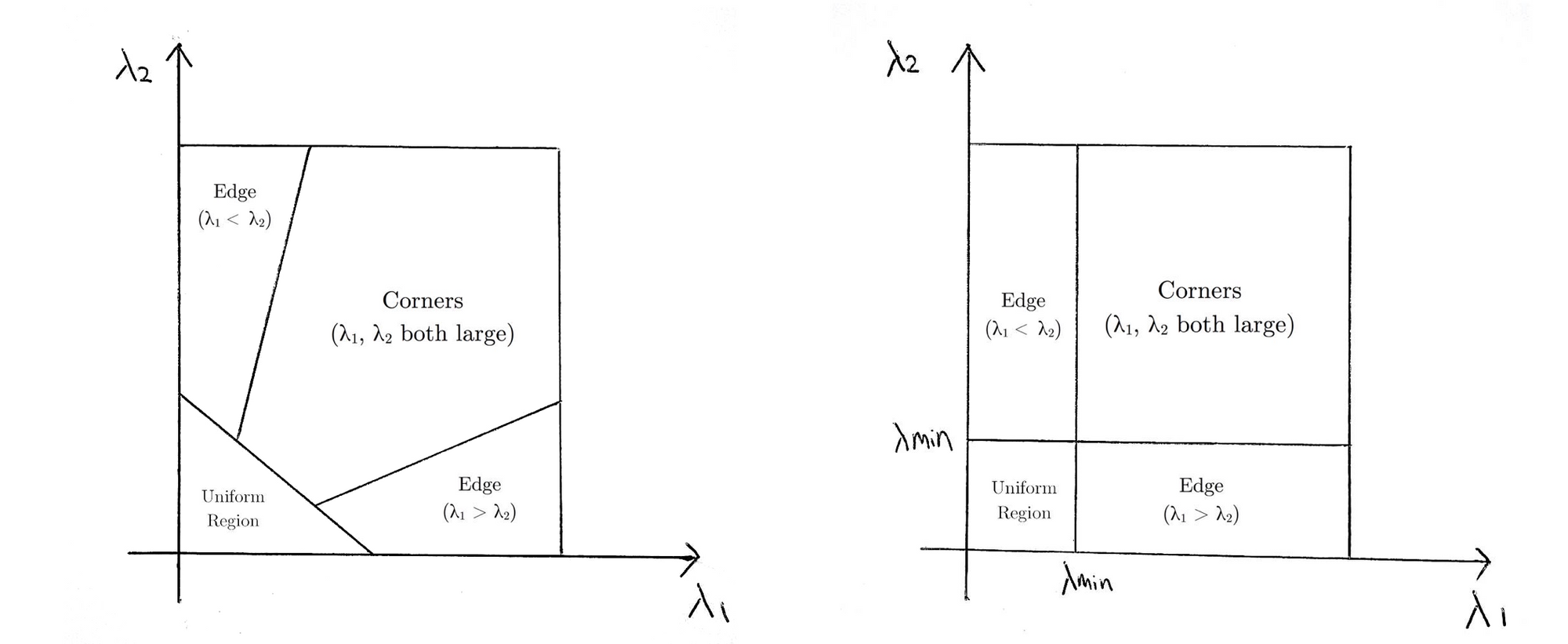
pentru Shi-Tomasi, numai atunci când \(01\) și \(X2\) sunt peste un prag minim \(x7min\) este fereastra clasificată drept colț.

documentația implementării Shi-Tomasi de către OpenCV pringoodFeaturesToTrack() poate fi găsită aici.

urmărirea obiectelor specifice

pot exista scenarii în care doriți să urmăriți doar un anumit obiect de interes (să zicem urmărirea unei anumite persoane) sau o categorie de obiecte (ca toate cele 2 vehicule wheeler în trafic). Puteți modifica cu ușurință codul pentru a urmări pixelii obiectelor dorite schimbând variabila prev.

de asemenea, puteți combina detectarea obiectelor cu această metodă pentru a estima doar fluxul de pixeli din casetele de delimitare detectate. În acest fel puteți urmări toate obiectele de un anumit tip/categorie din videoclip.

Lucas-Kanade: flux optic rar

Lucas și Kanade au propus o tehnică eficientă pentru a estima mișcarea caracteristicilor interesante prin compararea a două cadre consecutive în lucrarea lor o tehnică iterativă de înregistrare a imaginii cu o aplicație pentru viziunea Stereo. Metoda Lucas-Kanade funcționează sub următoarele ipoteze:

1. două cadre consecutive sunt separate printr-o mică creștere de timp (\(dt\)) astfel încât obiectele nu sunt deplasate semnificativ (cu alte cuvinte, metoda funcționează cel mai bine cu obiecte cu mișcare lentă).
2. un cadru descrie o scenă „naturală” cu obiecte texturate care prezintă nuanțe de gri care se schimbă fără probleme.

în primul rând, în aceste ipoteze, putem lua o fereastră mică 3×3 (cartier) în jurul caracteristicilor detectate de Shi-Tomasi și să presupunem că toate cele nouă puncte au aceeași mișcare.

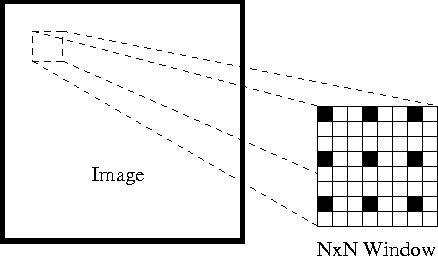
acesta poate fi reprezentat ca

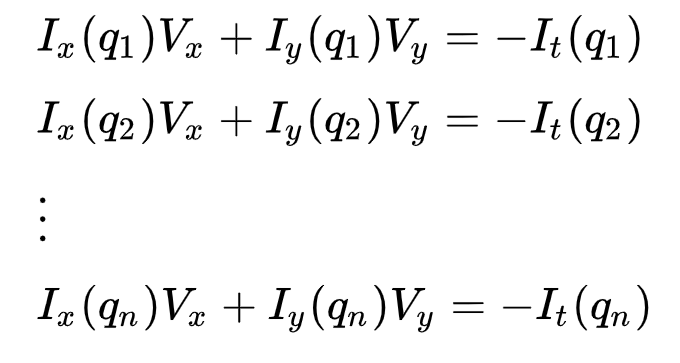
unde \(q_1, q_2, …, q_n\) denotă pixelii din interiorul ferestrei (de exemplu \(N\) = 9 pentru o fereastră 3×3) și \(i_x(q_i)\), \(i_y(q_i)\) și \(i_t(q_i)\) denotă derivatele parțiale ale imaginii \(i\) în raport cu poziția \((X, Y)\) și timpul \(T\), pentru pixel \(q_i\) la ora curentă.

aceasta este doar ecuația fluxului optic (pe care am descris-o mai devreme) pentru fiecare dintre n pixeli.

setul de ecuații poate fi reprezentat în următoarea formă de matrice unde \(Av = b\):

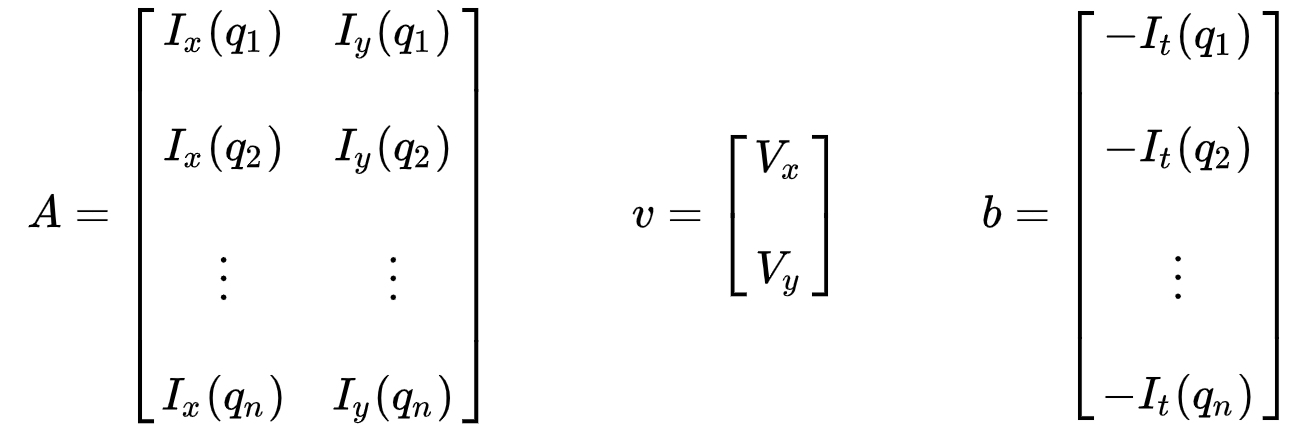
ia act de faptul că anterior (vezi „ce este fluxul optic?”secțiunea), ne-am confruntat cu problema de a trebui să rezolve pentru două variabile necunoscute cu o ecuație. Acum ne confruntăm cu rezolvarea a două necunoscute (\(V_x\) și \(V_y\)) cu nouă ecuații, care este supra-determinată.

În al doilea rând, pentru a aborda problema supra-determinată, aplicăm cele mai mici pătrate potrivite pentru a obține următoarea problemă cu două ecuații-două necunoscute:

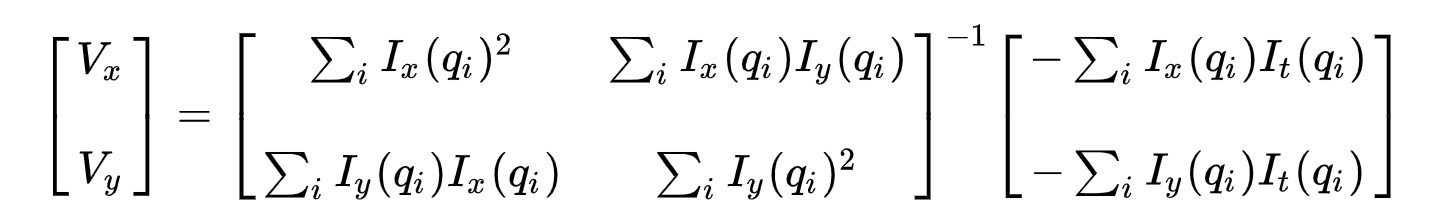
unde \(VX = u = DX/DT\) denotă mișcarea \(x\) în timp și \(Vy = v = dy / DT\) denotă mișcarea Y în timp. Rezolvarea pentru cele două variabile completează problema fluxului optic.

pe scurt, identificăm câteva caracteristici interesante pentru a urmări și calcula iterativ vectorii de flux optici ai acestor puncte. Cu toate acestea, adoptarea metodei Lucas-Kanade funcționează numai pentru mișcări mici (din presupunerea noastră inițială) și eșuează atunci când există mișcare mare. Prin urmare, implementarea OpenCV a metodei Lucas-Kanade adoptă piramide.

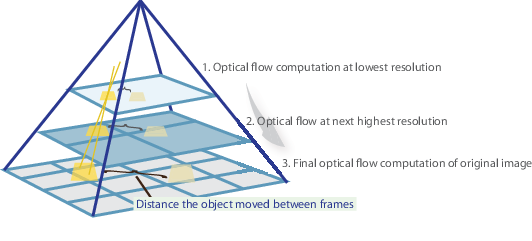
într-o vizualizare la nivel înalt, mișcările mici sunt neglijate pe măsură ce urcăm piramida și mișcările mari sunt reduse la mișcări mici – calculăm fluxul optic împreună cu scara. O explicație matematică cuprinzătoare a implementării OpenCV poate fi găsită în notele lui Bouguet și documentația implementării OpenCV a metodei Lucas-Kanade prin calcOpticalFlowPyrLK() poate fi găsită aici.

vizualizarea

și asta este! Deschideți terminalul și rulați

python sparse-starter.py

pentru a testa implementarea fluxului optic rar. în cazul în care ați pierdut vreun cod, codul complet poate fi găsit în sparse-solution.py.

implementarea fluxului optic dens

am calculat anterior fluxul optic pentru un set de caracteristici rare de pixeli. Fluxul optic dens încearcă să calculeze vectorul fluxului optic pentru fiecare pixel al fiecărui cadru. În timp ce un astfel de calcul poate fi mai lent, acesta oferă un rezultat mai precis și un rezultat mai dens, potrivit pentru aplicații precum structura de învățare din mișcare și segmentarea video. Există diferite implementări ale fluxului optic dens. Vom folosi metoda Farneback, una dintre cele mai populare implementări, folosind OpenCV, o bibliotecă open source de algoritmi de viziune computerizată, pentru implementare.

configurarea mediului

dacă nu ați făcut acest lucru deja, vă rugăm să urmați Pasul 1 de punere în aplicare a fluxului optic rare pentru a configura mediul.

apoi, deschide dense-starter.py cu editorul de text. Vom scrie tot codul în acest fișier Python.

Configurarea OpenCV pentru a citi un videoclip

Farneback Optical Flow

Gunnar Farneback a propus o tehnică eficientă pentru a estima mișcarea caracteristicilor interesante prin compararea a două cadre consecutive în lucrarea sa estimarea mișcării cu două cadre bazată pe expansiunea polinomială.

în primul rând, metoda aproximează ferestrele (vezi secțiunea Lucas Kanade a implementării fluxului optic RAR Pentru mai multe detalii) a cadrelor de imagine prin polinoame pătratice prin transformare de expansiune polinomială. În al doilea rând, observând modul în care polinomul se transformă sub traducere (mișcare), se definește o metodă de estimare a câmpurilor de deplasare din coeficienții de expansiune polinomială. După o serie de rafinări, se calculează fluxul optic dens. Lucrarea lui Farneback este destul de concisă și simplă de urmat, așa că vă recomand să parcurgeți lucrarea dacă doriți o mai bună înțelegere a derivării sale matematice.

pentru implementarea OpenCV, calculează magnitudinea și direcția fluxului optic dintr-o matrice cu 2 canale de vectori de flux \((dx/dt, dy/dt)\), problema fluxului optic. Apoi vizualizează unghiul (direcția) fluxului în funcție de nuanță și distanța (magnitudinea) fluxului în funcție de valoarea reprezentării culorilor HSV. Rezistența HSV este întotdeauna setată la maximum 255 pentru o vizibilitate optimă. Documentația implementării metodei Farneback de către OpenCV prin calcOpticalFlowFarneback() poate fi găsită aici.

vizualizarea

și asta este! Deschideți terminalul și rulați

python dense-starter.py

pentru a testa implementarea fluxului optic dens. în cazul în care ați pierdut vreun cod, codul complet poate fi găsit în dense-solution.py.

fluxul optic folosind învățarea profundă

în timp ce problema fluxului optic a fost istoric o problemă de optimizare, abordările recente prin aplicarea învățării profunde au arătat rezultate impresionante. În general, astfel de abordări iau două cadre video ca intrare pentru ieșirea fluxului optic (imagine codificată în culori), care poate fi exprimată ca:

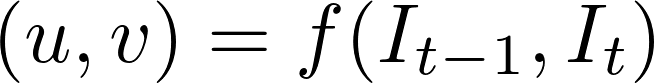
unde \(u\) este mișcarea în direcția \(x\), \(v\) este mișcarea în direcția \(y\), și \(f\) este o rețea neuronală care ia în două cadre consecutive \(i_{t-1}\) (frame at time = \(t-1)\) și \(i_t\) (frame at time = \(t)\) ca intrare.

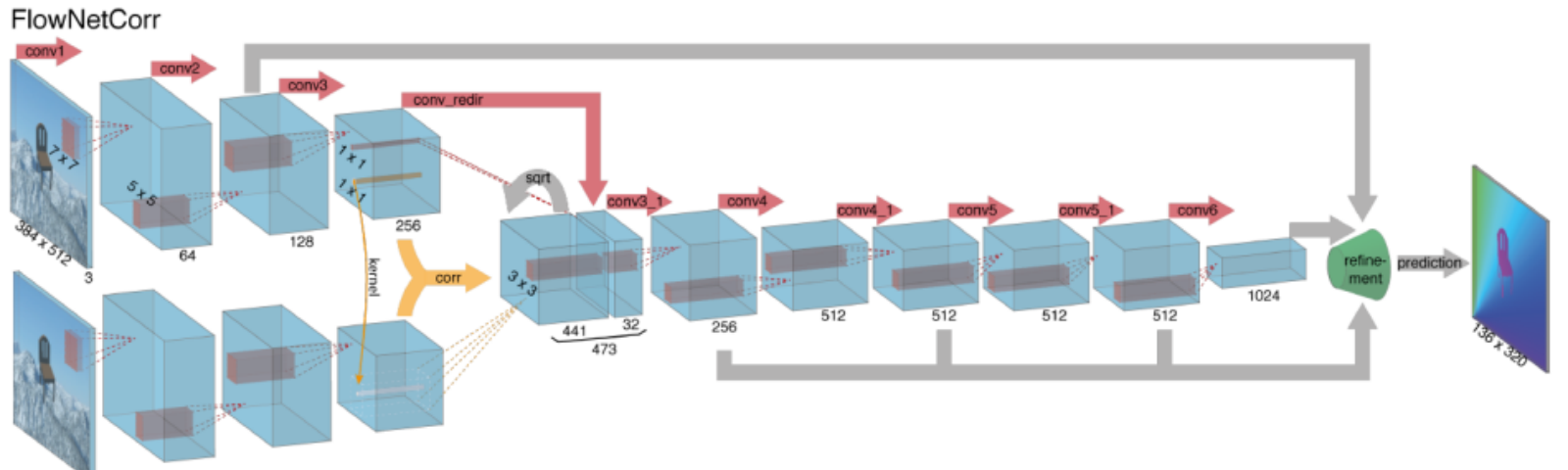
calculul fluxului optic cu rețele neuronale profunde necesită cantități mari de date de antrenament care sunt deosebit de greu de obținut. Acest lucru se datorează faptului că etichetarea înregistrărilor video pentru fluxul optic necesită determinarea exactă a mișcării exacte a fiecărui punct al unei imagini la precizia subpixelului. Pentru a aborda problema etichetării datelor de instruire, cercetătorii au folosit grafica computerizată pentru a simula lumi realiste masive. Deoarece lumile sunt generate de instrucțiuni, mișcarea fiecărui punct al unei imagini într-o secvență video este cunoscută. Câteva exemple de astfel de includ MPI-Sintel, un film CGI open-source cu etichetare a fluxului optic redat pentru diferite secvențe și scaune zburătoare, un set de date cu multe scaune care zboară pe fundaluri aleatorii, de asemenea, cu etichetare a fluxului optic.

rezolvarea problemelor de flux optic cu învățarea profundă este un subiect extrem de fierbinte în acest moment, cu variante de FlowNet, SPyNet, PwC-Net și multe altele care se depășesc reciproc pe diferite repere.

aplicarea fluxului optic: segmentarea semantică

câmpul fluxului optic este o vastă mină de informații pentru scena observată. Pe măsură ce tehnicile de determinare precisă a fluxului optic se îmbunătățesc, este interesant să vedem aplicații ale fluxului optic în joncțiune cu alte câteva sarcini fundamentale ale viziunilor computerului. De exemplu, sarcina segmentării semantice este de a împărți o imagine în serii de regiuni corespunzătoare claselor de obiecte unice, dar obiectele plasate îndeaproape cu texturi identice sunt adesea dificile pentru tehnicile de segmentare cu un singur cadru. Cu toate acestea, dacă obiectele sunt plasate separat, mișcările distincte ale obiectelor pot fi foarte utile în cazul în care discontinuitatea în câmpul dens de flux optic corespunde limitelor dintre obiecte.

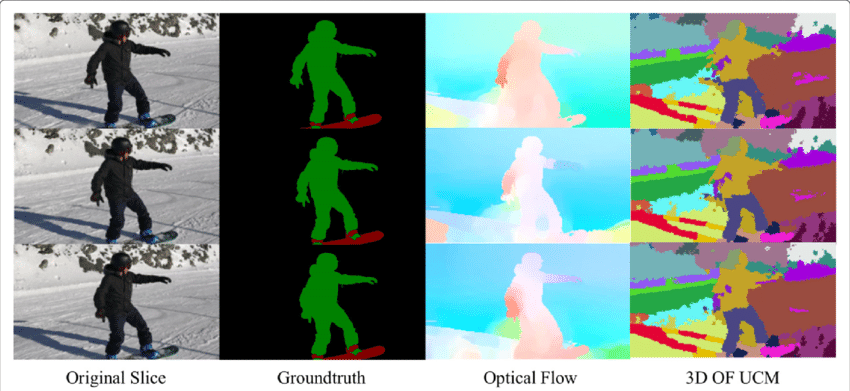
aplicarea fluxului optic: detectarea obiectelor& urmărirea

o altă aplicație promițătoare a fluxului optic poate fi detectarea și urmărirea obiectelor sau, într-o formă la nivel înalt, spre construirea sistemelor de urmărire a vehiculelor și de analiză a traficului în timp real. Deoarece fluxul optic rar utilizează urmărirea punctelor de interes, astfel de sisteme în timp real pot fi efectuate prin tehnici de flux optic bazate pe caracteristici, fie de la o cameră staționară, fie de la camere atașate vehiculelor.

concluzie

fundamental, vectorii de flux optic funcționează ca intrare la o multitudine de sarcini de nivel superior care necesită înțelegerea scenei secvențelor video, în timp ce aceste sarcini pot acționa în continuare ca blocuri de construcție pentru sisteme încă mai complexe, cum ar fi analiza expresiei faciale, navigarea autonomă a vehiculului și multe altele. Noile aplicații pentru fluxul optic încă de descoperit sunt limitate doar de ingeniozitatea designerilor săi.

leneș la cod, nu doriți să cheltuiți pe GPU-uri? Peste cap de la Nanonets și de a construi modele de viziune de calculator pentru drum liber!