AMS:: coloana caracteristică din AMS

postat iunie 2008.
geometria planimetrului
Teorema lui Guldin
rezultatul complet
Planimetrele și teorema lui Green
alte tipuri de planimetre
pentru a afla mai multe

postat iunie 2008.

a doua dintre cele două coloane despre matematica topografiei (prima este aici). …

Bill Casselman
Universitatea din British Columbia, Vancouver, Canada
cass la math.ubc.ca

John Eggers
Universitatea din California, San Diego
jeggers la ucsd.edu

e-Mail unui prieten

tipăriți acest articol

un planimetru este un instrument de masă pentru măsurarea zonelor, de obicei zonele regiunilor neregulate de pe o hartă sau fotografie. Acestea au fost odată comune, dar acum au fost în mare parte înlocuite cu instrumente digitale.

următoarea imagine oferă o idee despre configurare. Brațul stâlpului se rotește liber în jurul stâlpului, care este fixat pe masă. Brațul trasor se rotește în jurul pivotului, unde se alătură brațului polar. Urmăriți o curbă în sensul acelor de ceasornic cu trasorul și, pe măsură ce faceți acest lucru, roata de măsurare se rostogolește, iar distanța totală pe care o rulează este acumulată pe cadran. Roata de sprijin împiedică lucrul să se răstoarne. La sfârșit, citiți un număr de pe cadran și, după înmulțirea cu un factor care depinde doar de configurația particulară a planimetrului, obțineți zona din interiorul curbei.

următoarea figură vă oferă o imagine mai bună a mecanismului.

noi numim căruciorul ansamblul de roți, cadran, și pivot. În imaginea următoare veți obține o privire mai bună la ea, și se poate vedea unitatea vierme care face ca cadranul să se rotească ca se mișcă roata de măsurare.

Iată diagrama planimetrului original, din articolul lui Jakob Amsler care l-a introdus:

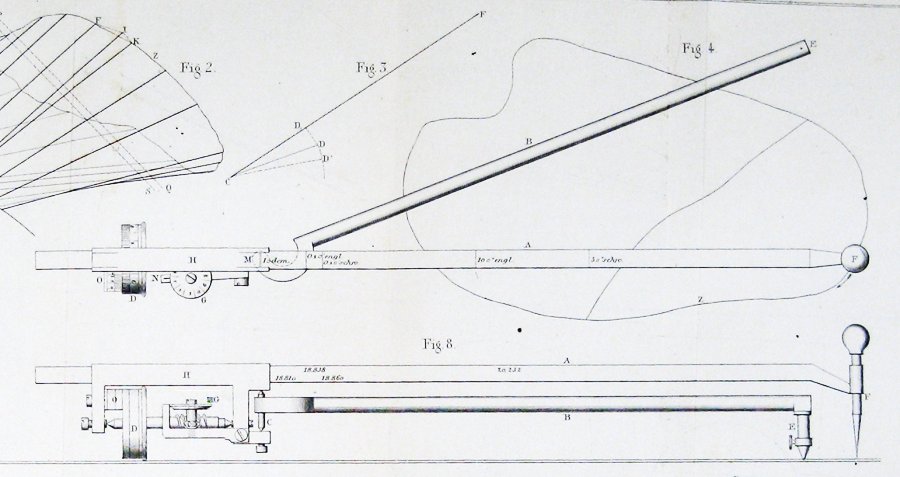
cum poate un lucru atât de simplu să măsoare zonele?

geometria planimetrului

mișcarea în sensul acelor de ceasornic a planimetrului este direcția opusă a ceea ce matematicienii au decis că ar trebui să fie rotația pozitivă. În loc să încălcăm această convenție, vom lucra de acum înainte cu un planimetru matematician, în care vă deplasați în sens invers acelor de ceasornic. Ca și fanteziile altor matematicieni, nu există pe planetă!

există câteva restricții cu privire la modul de plasare a planimetrului în raport cu curba pe care doriți să o urmăriți. Trăsura poate fi glisată de-a lungul brațului trasorului, dar în toate cazurile lungimea l a brațului trasorului este mai mică decât lungimea r a brațului stâlpului. Aceasta înseamnă că trasorul nu poate ajunge niciodată la o distanță r – l de pol. Pe de altă parte, atunci când este complet extins, trasorul nu poate ajunge niciodată dincolo de r + l. deci curba care trebuie urmărită trebuie să se afle în inelul dintre două cercuri, unul cu raza r – l, celălalt r + l.

de fapt, ar trebui să devină clar într-o clipă că brațele nu ar trebui niciodată extinse complet, astfel încât curba care trebuie urmărită trebuie să se afle complet în interiorul inelului. În plus, în mod normal, polul este plasat pe exteriorul curbei.

pentru un anumit punct din inel există exact două configurații posibile ale planimetrului care plasează trasorul pe acel punct. Alegerea unui punct sau a celuilalt înseamnă alegerea unui semn pentru o rădăcină pătrată. Numim aceasta alegerea unei orientări pentru planimetru. Este pozitiv dacă rădăcina pătrată este pozitivă. Odată aleasă o orientare, aceasta va rămâne aceeași, cu excepția cazului în care brațul este complet extins. Asta nu trebuie să se întâmple niciodată. Atâta timp cât curba dvs. este în întregime în interiorul inelului, configurațiile planimetrului vor varia lin și unic cu calea trasorului.

următorul lucru de făcut este să înțelegem câteva lucruri despre mișcarea roții de măsurare. După cum arată imaginea de mai jos, dacă roata se deplasează în linie dreaptă la o distanță C, roata se rotește printr-un unghi XQ = C/R unde R este raza sa.

deci, este adevărat că rotația roții și distanța parcursă de brațul trasorului au o relație între ele. Dar această relație este un pic subtilă. Dacă brațul se mișcă drept înainte la o distanță C, zona măturată va fi lC, dar dacă se deplasează paralel cu ea însăși, zona măturată va fi 0. În primul caz, un punct de pe circumferința roții se va deplasa la distanța C. În al doilea caz, roata nu se va mișca deloc. Și dacă brațul se traduce oblic, roata se va roti la o distanță egală cu altitudinea paralelogramului acoperit de braț. În toate cazurile în care brațul se traduce paralel cu el însuși, zona măturată de porțiunea brațului trasorului dintre pivot și trasor va fi egală cu lC, unde C este distanța măsurată prin rotația roții. Acesta este faptul de bază care leagă mișcarea brațului de mișcarea roții de măsurare.

modalitatea de a formula acest lucru este tocmai aceea că, indiferent de modul în care brațul se mișcă, distanța măsurată de roată este calea integrală

În cazul în arm în orice moment și T este Vectorul unitar îndreptat în direcția de deplasare (astfel încât, de exemplu, dacă brațul se mișcă paralel cu el însuși, produsul punct al lui N și T este 0).

Teorema lui Guldin

în continuare vom încerca să facem comportamentul planimetrului intuitiv clar, dar mai întâi vom privi un tip special de planimetru și, în acest caz, vom dovedi un rezultat mai general. Să presupunem că luăm un singur braț în mișcare liberă de lungime l și îi atașăm o roată de măsurare a razei R chiar în centrul său.

apoi mișcăm brațul în jurul avionului. În cazul în care roata de măsurare se rotește printr-un unghi total de radiani centimetrici pe măsură ce brațul se deplasează, distanța parcursă de un punct pe circumferință este c = ectr.Teorema lui Guldin. În această situație, suprafața totală măturată de braț este produsul lC.

zona de aici este interpretată cu un semn. Dacă brațul se rotește doar în jurul centrului său, o jumătate a brațului merge înainte și cealaltă înapoi, iar cele două se anulează.

am văzut deja că afirmația lui Guldin este valabilă în cazul în care brațul doar se traduce. Desigur, acest lucru nu se întâmplă întotdeauna – brațul se poate roti pe măsură ce se mișcă și se poate traduce. Dar putem vedea ce se întâmplă tăind zona măturată după cum urmează:

deoarece roata de măsurare se află în centrul brațului, pe măsură ce brațul se rotește, acesta strivește blocurile mici pe o parte pe măsură ce le extinde pe cealaltă. Aceste efecte se anulează reciproc exact.

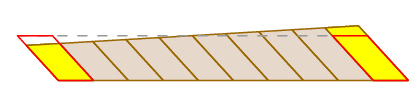
o dovadă complet riguroasă poate fi dată folosind formula pentru schimbarea variabilelor într-o integrală dublă și expresia pentru deplasarea roților ca integrală de cale.

acum să presupunem că roata este plasată în altă parte. Spuneți că poziția sa este c + v unde c este centrul brațului și v un vector de-a lungul brațului. Lungimea lui v va rămâne fixă, să zicem la hectar. Calea pe care o urmează roata este c(t) + v(t). Integrala de cale este acum

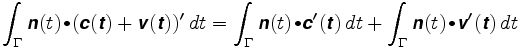
prima integrală este distanța pe care roata ar parcurge-o dacă ar fi în centrul brațului. În al doilea, vectorul v(t) este întotdeauna perpendicular pe n, iar v(t) are o lungime constantă. Vectorul v (t) se deplasează în jurul unui cerc de rază egal cu centimetrul. Prin urmare, produsul punct al lui n și v'(t) este doar lungimea semnată a lui v'(t), iar a doua integrală este egală cu de opt ori rotația totală a brațului. Prin urmare:

dacă roata se află la o distanță de la centrul brațului, distanța C pe care Roata o măsoară este C0 , distanța care ar fi măsurată dacă roata ar fi în centru, plus de la un unghi de la un unghi total de la un unghi de la un unghi total de la un unghi de la un unghi total de la un unghi total de la un unghi de rotație al brațului.

puteți vedea imediat un caz simplu de acest lucru prin rotirea brațului în jurul centrului său. Combinând acest lucru cu Teorema lui Guldin, vedem că în toate cazurile:

C = C0 + XV
zona măturată = l C0 = l C – l

rezultatul complet

formula lui Guldin oferă o zonă semnată – dacă măturați înapoi peste o zonă, roata merge înapoi și anulați zona pe care ați acoperit-o deja. Dacă aplicăm acest lucru în cazul în care brațul liber se întoarce exact de unde a început, vedem că lC este egal cu aria regiunii închise trasată de capătul drept al brațului minus cea a regiunii măturate de cea stângă.

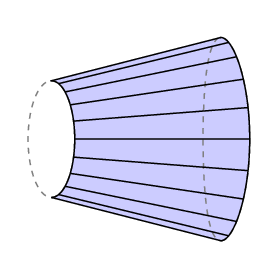
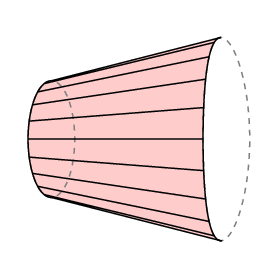
în cazul planimetrului polar, partea inferioară a brațului este limitată la un arc al cercului de rază r cu Centrul la pol, prin urmare l C este zona trasată de trasor. În plus, în mod normal, Polul se află în afara regiunii de măsurat și, în acest caz, cantitatea totală de rotație a brațului trebuie să fie 0. Deci, în acest caz avem

zona regiunii trasată = lC

iată figura inclusă de Jakob Amsler, inventatorul, în lucrarea sa originală despre instrumentul pe care l-a inventat:

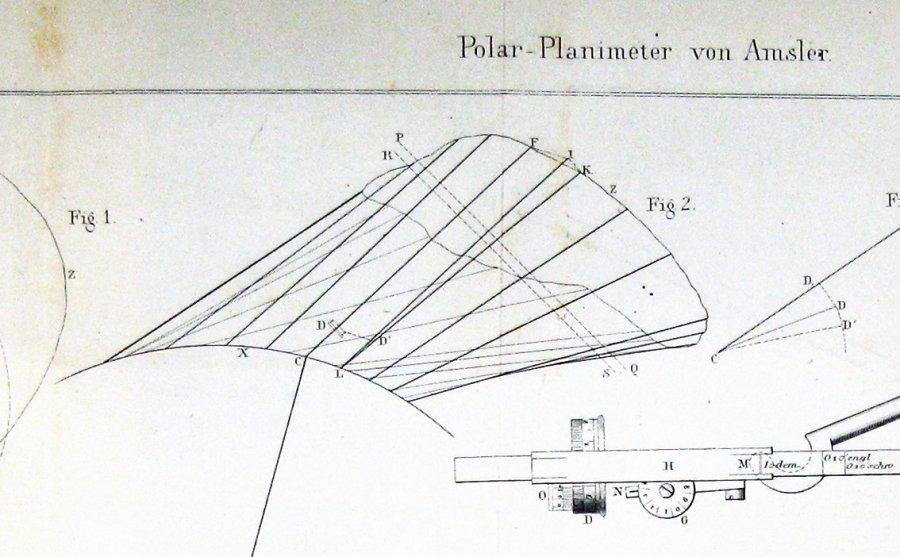
pare destul de clar din aceasta că Amsler și-a derivat construcția printr-o formă a teoremei lui Guldin.

Planimetrele și teorema lui Green

după cum am menționat deja, după ce am ales orientarea planimetrului, configurația planimetrului este o funcție continuă a poziției trasorului. Să zicem că alegem orientarea pozitivă. Apoi putem atașa la fiecare punct al inelului un vector unitar n, cel îndreptat în sens invers acelor de ceasornic și perpendicular pe brațul trasorului la trasor.

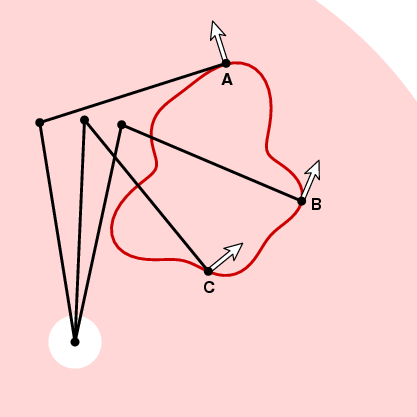
modul în care roata de măsurare va răspunde la mișcarea de-a lungul curbei în următoarea clipă depinde de unghiul dintre acest vector și vectorul unitate tangentă al curbei. La A din imaginea de mai sus, roata de măsurare nu se va mișca, deoarece mișcarea de-a lungul curbei este paralelă cu brațul trasorului. La B dacă trasorul se deplasează la o distanță mică ds, la fel și roata de măsurare. Și la C roata de măsurare se va deplasa o anumită distanță între 0 și ds. Pentru a fi mai precis, să presupunem că t este unitatea vector tangent la un moment dat al curbei. Dacă trasorul deplasează distanța ds de-a lungul curbei, în acel moment roata de măsurare va deplasa o distanță d ds, unde d = n . t, produsul punct al vectorilor unitari t și n. cu alte cuvinte, dacă ne deplasăm în jurul curbei XQ roata de măsurare se va deplasa la o distanță totală egală cu integrala lui n . t ds (dot product), sau

dar din moment ce fiecare punct al inelului corespunde unei configurații pozitive unice a planimetrului, putem atribui un vector n fiecărui punct interior al inelului și, prin urmare, definește un câmp vectorial. Curba de la A La Z este limita interiorului său de la A La Z, iar prin una dintre ipotezele noastre aceasta este conținută în întregime în regiunea în care n este definită. Teorema lui Green ne spune că integrala căii în jurul graniței acestei regiuni este, de asemenea, egală cu o anumită integrală peste hectar: Prin urmare

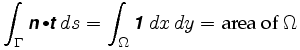
Mai exact, Teorema lui Green ne spune că

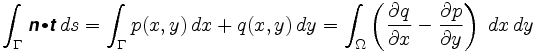
unde n = este câmpul vectorial implicat. Integrandul din integrala dublă se numește ondularea câmpului vectorial.

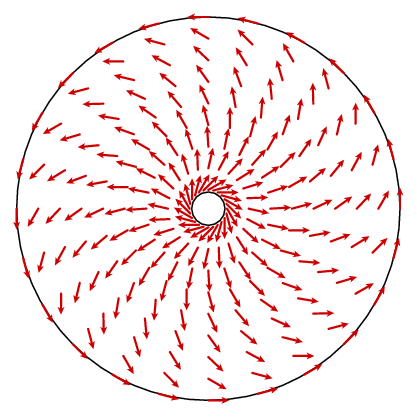
Acest lucru nu pare să ne ducă prea departe. Ceea ce ar trebui să se întâmple este că curl este o constantă 1. În principiu, am putea găsi o formulă pentru câmpul vectorial n și să-i calculăm ondularea, dar acest lucru nu este foarte edificator. Cu toate acestea, putem profita de un alt fapt. Câmpul vectorial are simetrie circulară, ceea ce înseamnă că este determinat de ceea ce este pe o rază. Legea cosinusului ne oferă o formulă simplă pentru componenta circumferențială.

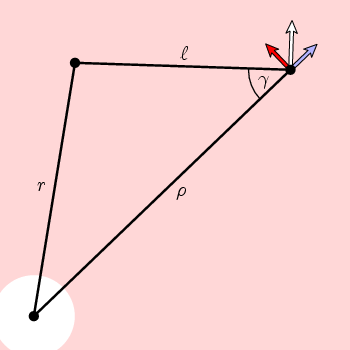
rezultă din geometria simplă din această figură că componenta circumferențială a lui n este

f(circulant) = cos(circulant) = (circulant 2 + l 2 – r 2)/(2 circulant l)

punctul real al teoremei lui Green este că, pentru a verifica dacă integrandul este 1, este suficient să se verifice dacă integrala căii în jurul unor la fel ca zona. Pentru aceasta, alegem regiunile noastre să fie ca aici:

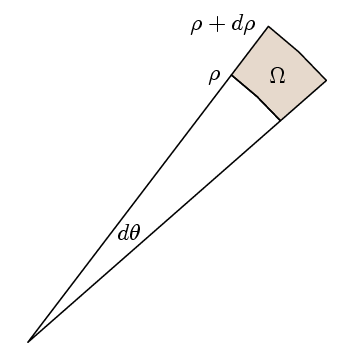
Apoi l ori integral calea este

l (ρ+dp)( f(ρ+dp)- f(ρ) ) dθ

(θ/2) ( (ρ + dp) 2 – ρ 2)

care este zona de regiune Ω.

alte tipuri de planimetre

Teorema lui Guldin implică faptul că mișcarea unei roți de măsurare vă va spune zona trasată de trasor ori de câte ori brațul cu o roată de măsurare pe ea trasează o curbă, dar are un capăt limitat la o curbă unidimensională. Acest lucru se întâmplă, de exemplu, cu planimetrul de rulare, în care pivotul este limitat la o linie dreaptă, fiind pe un cilindru de rulare.

pentru a afla mai multe

încă face și vinde planimetre.
volumul de calcul diferențial și Integral II, R. Courant, Blackie& Son, 1936. Secțiunea despre Formula lui Guldin (PP.294-298) oferă o explicație a modului în care funcționează planimetrul.articolul original al lui Amsler, Vierteljahresschrift der Naturforschenden Gesellschaft în Zuerich, 1856. Aici lipsesc diagramele, dar ele sunt aici:
- prima diagramă a lui Amsler
- a doua diagramă a lui Amsler
mulțumim Donnei Sammis de la Biblioteca Universității Stony Brook pentru localizarea articolului și soțului ei Robert pentru furnizarea de fotografii ale figurilor.

compania pe care Amsler a fondat-o a produs instrumente până în secolul 20. Această fotografie prezintă logo-ul, pe o versiune pantograf a planimetrului:
„despre Planimetre,” EngineerSupply. Compania a postat și un videoclip pe YouTube.