Franck-Condon-principen beskriver intensiteten hos vibroniska övergångar, eller absorptionen eller emissionen av en foton. Den säger att när en molekyl genomgår en elektronisk övergång, såsom jonisering, upplever molekylens kärnkonfiguration ingen signifikant förändring. Detta beror faktiskt på att kärnor är mycket mer massiva än elektroner och den elektroniska övergången sker snabbare än kärnorna kan svara. När kärnan anpassar sig till den nya elektroniska konfigurationen säger teorin att den måste genomgå en vibration.
om vi föreställer oss den vertikala övergången från jord till exciterat elektroniskt tillstånd som inträffar från en vibrationell vågfunktion som ger en sannolikhetsfördelning för att hitta kärnorna i ett geområde i rymden kan vi bestämma sannolikheten för en given vibrationsnivå från överlappningsintegralen \(s_{v’,v}\) som ger överlappningen av vibrationsvågfunktionen i marken och exciterat tillstånd. \ (V’\) kvantnummer hänvisar till marktillståndet och \(v\) kvantnummer hänvisar till det upphetsade tillståndet. Övergångssannolikheten kan separeras i elektroniska och nukleära delar med hjälp av Condon approximationen.
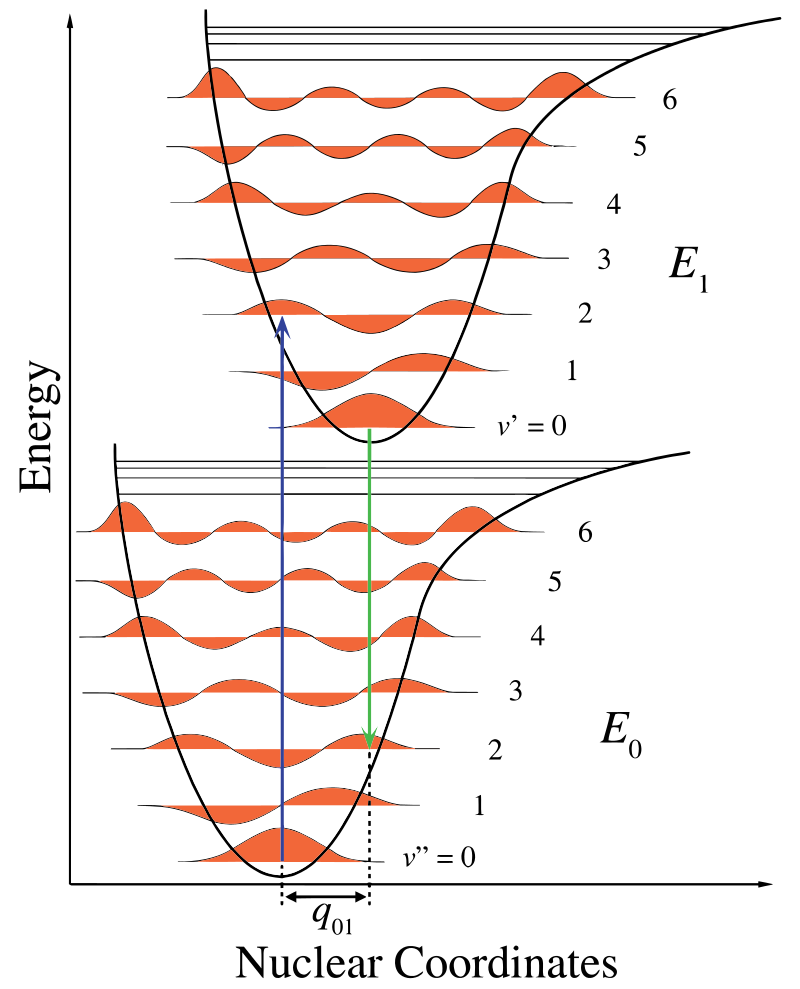
i Figur \(\PageIndex{1}\) visar kärnaxeln en följd av internukleär separation och den vibroniska övergången indikeras av de blå och gröna vertikala pilarna. Denna siffra visar tre saker:
- en absorption leder till ett högre energitillstånd,
- fluorescens leder till ett lägre energitillstånd och
- skiftet i kärnkoordinaterna mellan marken och det upphetsade tillståndet indikerar en ny jämviktsposition för kärninteraktionspotential. Det faktum att fluorescenspilen är kortare än absorptionen indikerar att den har mindre energi eller att dess våglängd är längre.
den klassiska Condon approximationen
Condon approximation är antagandet att den elektroniska övergången sker på en tidsskala kort jämfört med kärnrörelse så att övergångssannolikheten kan beräknas vid en fast kärnposition.
denna förändring i vibrationer upprätthålls under ett tillstånd som kallas snabb elektronisk excitation. De resulterande Coulombic krafterna producerar en jämvikt som visas i figuren för kärnorna som kallas en vändpunkt. Vändpunkten kan kartläggas genom att dra en vertikal linje från minsta nedre kurva till skärningspunkten för det högre elektroniska tillståndet. Denna procedur kallas en vertikal övergång och diskuterades tidigare i samband med fotoelektronspektroskopi (en annan elektronisk spektroscoy)..
Franck-Condon-principen förklarar de relativa intensiteterna för vibroniska övergångar genom att relatera sannolikheten för en vibrationell övergång till överlappningen av vibrationsvågfunktionerna. Det anges att sannolikheten för en vibrationsövergång som inträffar vägs av Franck-Condon-överlappningsintegralet:
\
inom Franck-Condon-approximationen anses kärnorna vara ”fasta” under elektroniska övergångar. Således kan elektroniska övergångar betraktas som vertikala övergångar på elektroniska potentiella energikurvor (vieriska övergångar i Figur \(\PageIndex{1}\)).
Quantum Franck-Condon-principen
Franck-Condon-principen har både en klassisk och Kvantapplikation. Klassiskt är Franck-Condon-principen approximationen att en elektronisk övergång sannolikt kommer att ske utan förändringar i kärnans positioner i molekylenheten och dess miljö. Det resulterande tillståndet kallas ett Franck-Condon-tillstånd, och övergången involverad, en vertikal övergång. Den kvantmekaniska formuleringen av denna princip är att intensiteten hos en vibronisk övergång är proportionell mot kvadraten av överlappningsintegralet mellan vibrationsvågfunktionerna i de två tillstånden som är involverade i övergången.
Franck-Condon-principen är baserad på Born-Oppenheimer-approximationen, som möjliggör separation av de elektroniska \(q\) och nukleära \(Q\) vågfunktionerna med tanke på den totala vågfunktionen.
\
eftersom övergångsoperatören, \(\hat{\mu}(q)\), endast är beroende av den elektroniska komponenten, kan kärnkomponenterna separeras från övergångsmomentets integral som dikterar sannolikheten för övergången:
&= \underbrace{ \langle \psi^{*}_{NUC, f} | \psi_{NUC, i} \rangle}_{\text{nukleär överlappning}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle \end{align}\]
om den nukleära överlappningsintegralen är noll för denna övergång, kommer övergången inte att observeras, oavsett storleken på den elektroniska faktorn.
\(S_{00}\) övergång utvärderad inom harmonisk Oscillatormodell
kärnöverlappningen för noll-nollövergången \(s_{00}\) kan beräknas helt enkelt med hjälp av definitionen av Gaussisk form av harmoniska oscillatorvågfunktioner.
nollpunktsvågfunktionen i det elektroniska jordtillståndet är
\
nollpunktsvågfunktionen i det upphetsade elektroniska tillståndet är
\
där
- \(\alpha = \dfrac{\sqrt{mk}}{\hbar}\)
- \(r_e\) är jämviktsbindningslängden i jordelektroniskt tillstånd
- \(q_e\) är jämviktsbindningslängden i det upphetsade elektroniska tillståndet
den nukleära överlappningsintegralen är
\
exponenten i ekvationen \(\ref{FC1}\) kan utökas som
\
och vi använder
\
och
\
för att ersätta och slutföra torget inuti integralet. Vi kan uttrycka
\.\ ]
således är integralen i ekvationen \(\ref{FC2}\)
\
integralen är en Gaussisk integral. Du kan visa att om vi låter \(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\) då \(dz = \sqrt{\alpha} dR\) och integralen blir
\
denna integral har redan lösts, från en tabell med integraler blir ekvation \(\ref{FC3}\)
\
Vi skulle följa samma procedur för att beräkna överlappningen av nollnivåvibrationen i marken till den första upphetsade vibrationsnivån i det upphetsade tillståndet: \(s_{01}\).
\(S_{01}\) övergång utvärderad inom harmonisk Oscillatormodell
för att beräkna överlappningen av zeroth marktillståndsnivå (\(v=0\)) med den första upphetsade tillståndsnivån (\(v’=1\)) använder vi Hermite polynom \(H_1(x) =2x\) för att beskriva den upphetsade tillståndsvågfunktionen (se här för en översyn av harmoniska oscillatorvågfunktioner). Här \(x = \ sqrt{\alpha} (R – Q_e)\).
\
med nollpunktsvågfunktionen i marken elektroniskt tillstånd är
\
den första upphetsade vågfunktionen i det upphetsade elektroniska tillståndet är
\
överlappningen av zeroth marktillståndsnivå med den första upphetsade tillståndsnivån (ekvation \(\ref{fc01}\)) är då
\
och
\
samma substitutioner kan göras som ovan så att integralen kan skrivas som (visas inte och att demonstreras i en läxa övningar) och slutresultatet är
\
Vi kunde fortsätta och beräkna den överlappningen av nollnivån i marktillståndet med alla högre vibrationsnivåer: \(S_{02}\), \(s_{03}\), etc. Varje term motsvarar en övergång med en annan energi eftersom vibrationsnivåerna har olika energier. Absorptionsbandet uppträder sedan av en progression (En Franck-Condon-progression) av övergångar mellan olika nivåer var och en med sin egen Sannolikhet.
Franck-Condon Progressions
för att förstå betydelsen av ovanstående formel för FC-faktorn, låt oss undersöka en mark och upphetsad tillståndspotential energiyta vid \(T = 0\) Kelvin. Nedan visas två tillstånd separerade med 8000 cm-1 i energi. Detta är energiseparation mellan botten av deras potentiella brunnar, men också mellan respektive nollpunktsenerginivåer. Låt oss anta att vågantalet för vibrationsläget är 1000 cm-1 och att bindningslängden ökas på grund av det faktum att en elektron avlägsnas från en bindningsbana och placeras i en antibindningsbana vid elektronisk excitation.
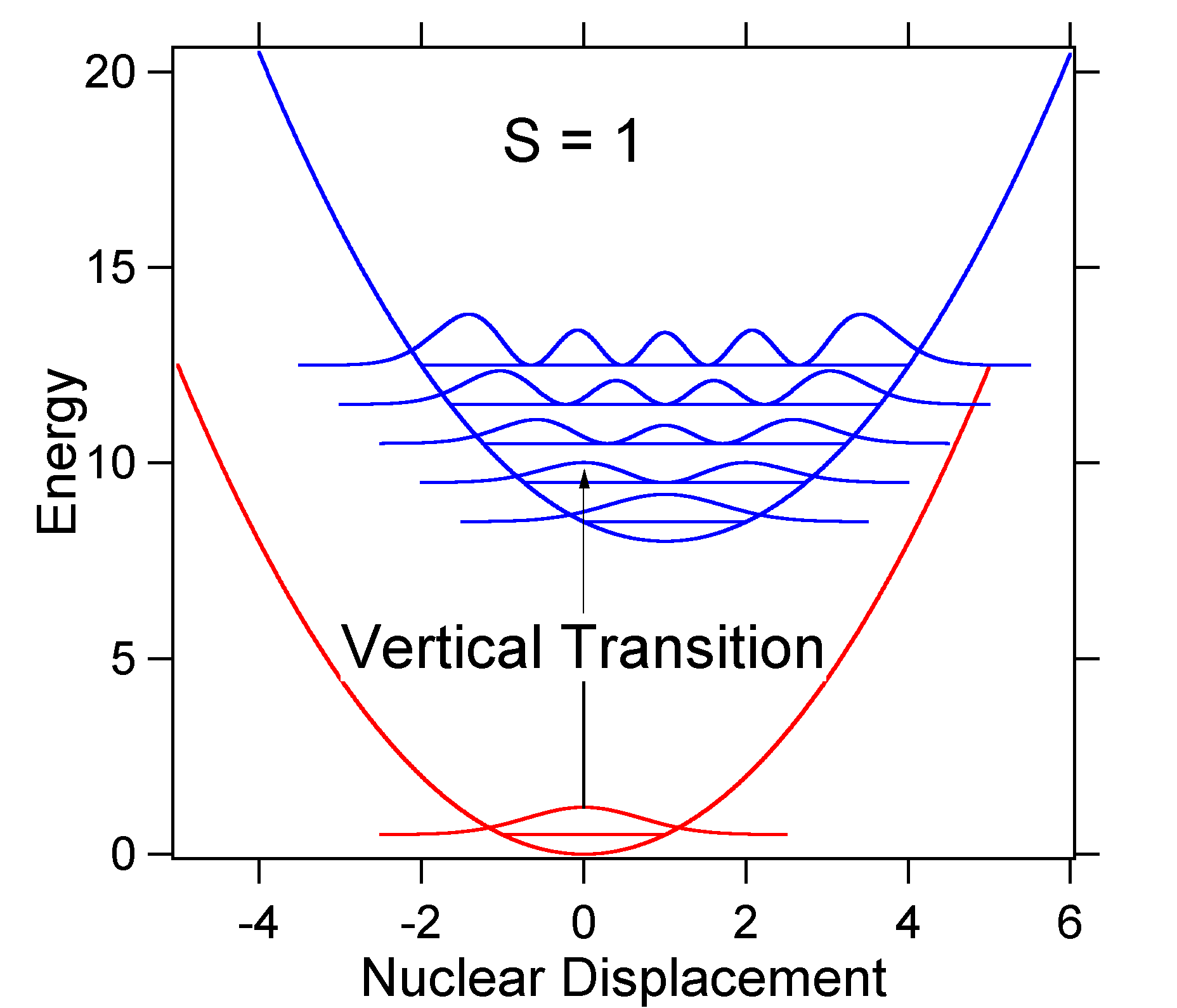
enligt ovanstående modell för Franck-Condon-faktorn skulle vi generera ett” stick ” – spektrum (figur \(\PageIndex{3}\)) där varje vibrationsövergång är oändligt smal och övergången kan bara ske när \(E = h\nu\) exakt. Till exempel gavs de potentiella energiytorna för S = 1 och övergångssannolikheten vid varje nivå ges av pinnarna (svart) i figuren nedan.
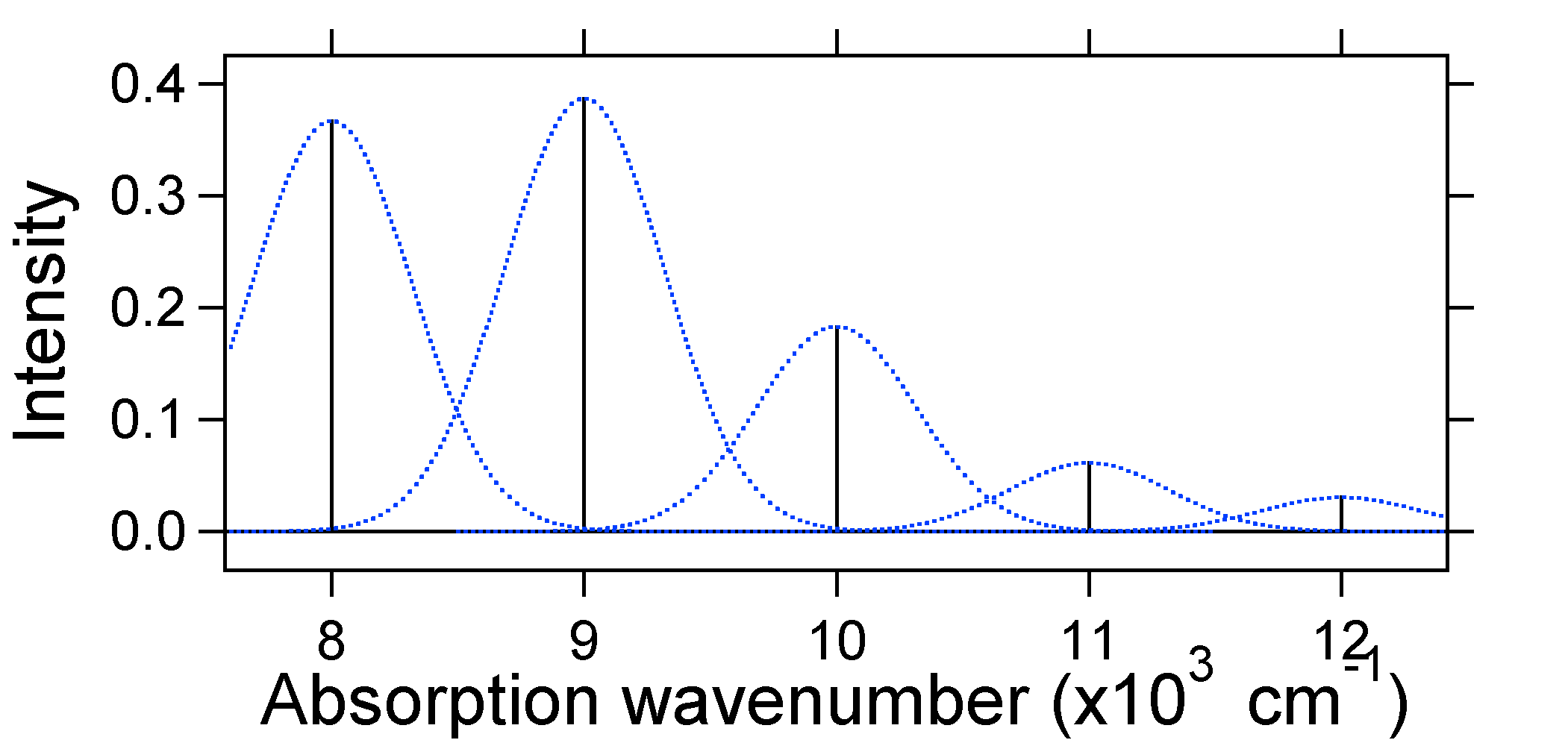
de prickade Gaussierna som omger varje pinne ger en mer realistisk bild av hur absorptionsspektret ska se ut. För det första kommer varje energinivå (pinne) att ges en viss bredd av det faktum att staten har en begränsad livslängd. Sådan breddning kallas homogen breddning eftersom den påverkar alla molekyler i ensemblen på ett liknande sätt. Det finns också breddning på grund av små skillnader i miljön för varje molekyl. Denna typ av breddning kallas inhomogen breddning. Oavsett ursprung skapades modellen ovan med hjälp av en Gaussisk breddning
kärnförskjutningen mellan marken och det upphetsade tillståndet bestämmer formen på absorptionsspektrumet. Låt oss undersöka både en mindre och en stor upphetsad tillståndsförskjutning. Om \(s = 0B) och de potentiella energiytorna i detta fall är:
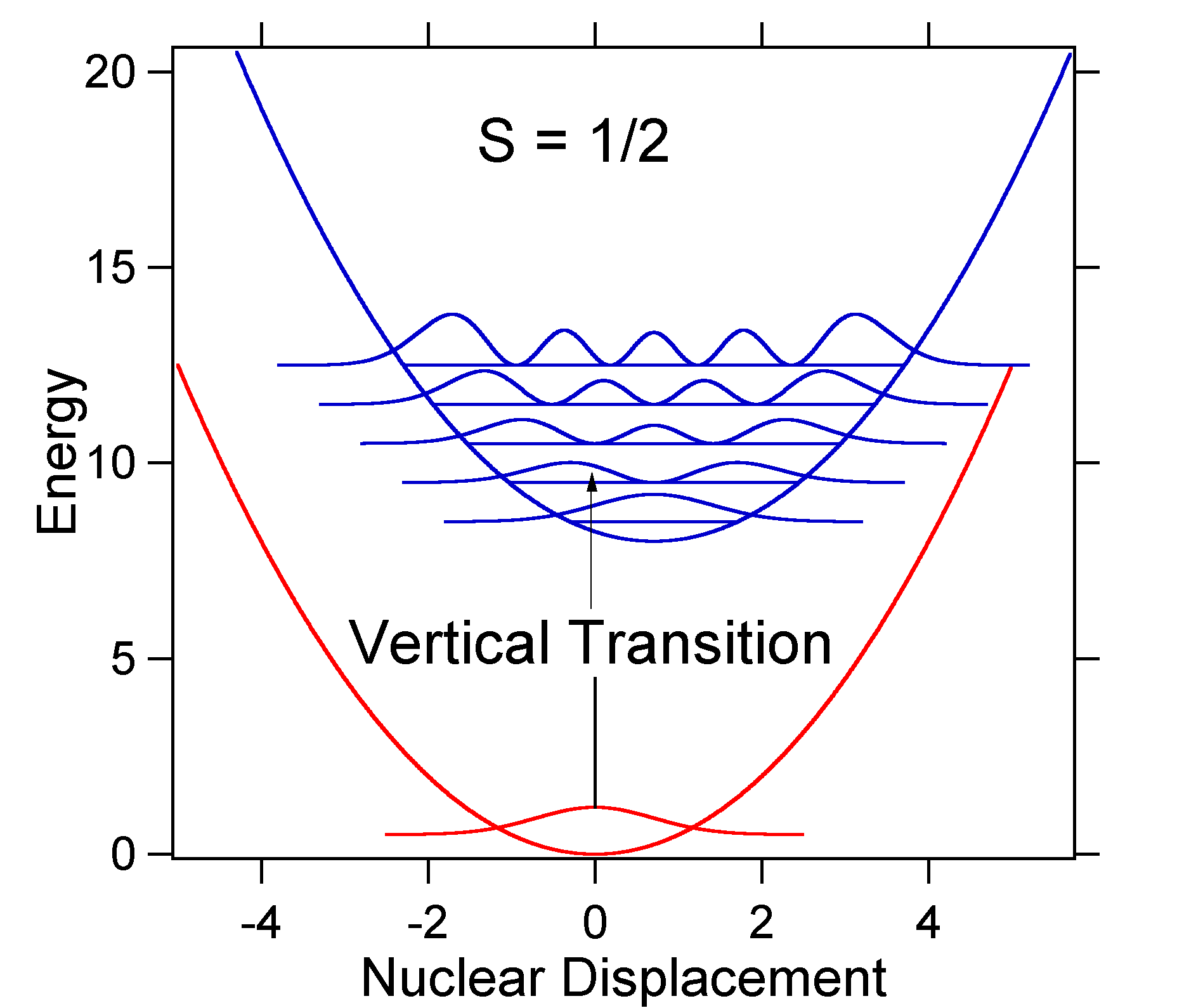
For this case the ”stick” spectrum has the appearance in Figure \(\PageIndex{5}\)
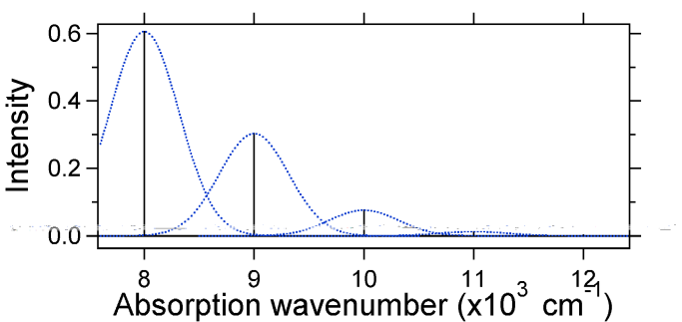
Observera att noll-noll eller \(s_{0,0}\) vibrationsövergång är mycket stor i det fall där förskjutningen är liten.
som en allmän tumregel ger \(S\) konstanten förhållandet mellan intensiteten för övergången \(v = 2\) till övergången \(v = 1\). I detta fall sedan \(S = 0,5\) är \(v=2\) övergången 0,5 intensiteten av \(v=1\) övergång.
som ett exempel på en större förskjutning visas dispositionen av de potentiella energiytorna för S = 2 nedan.
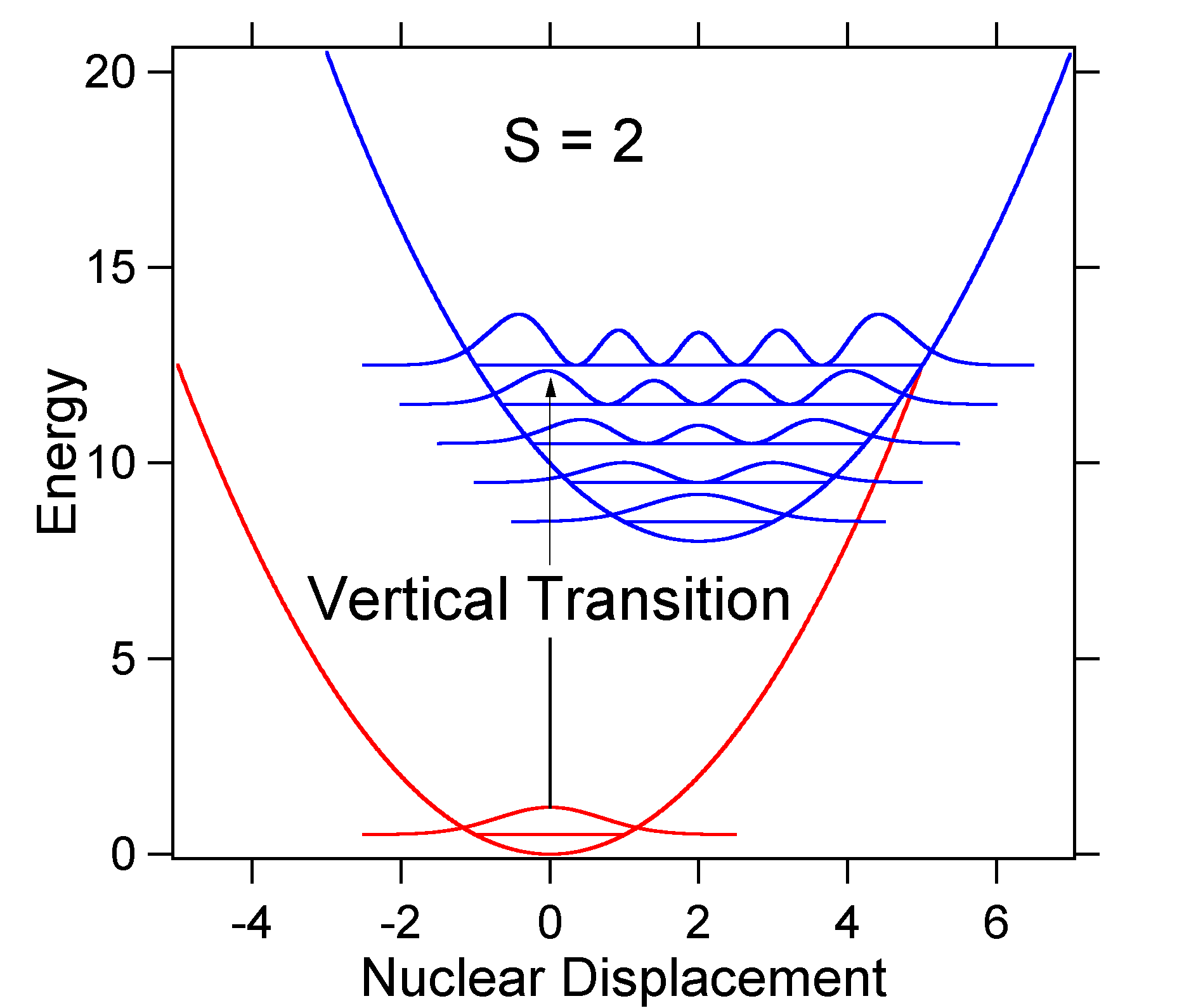
den större förskjutningen resulterar i minskad överlappning av marktillståndsnivån med V = 0-nivån i det upphetsade tillståndet. Den maximala intensiteten uppnås i högre vibrationsnivåer som visas i stickspektrumet.
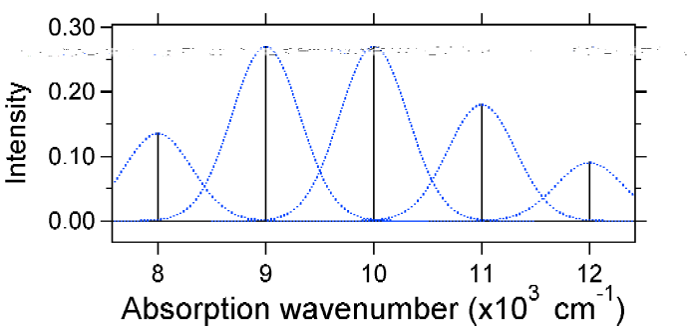
absorptionsspektra som plottas nedan har alla samma integrerade intensitet, men deras former förändras på grund av den olika graden av förskjutning av den exciterade tillståndets potentiella energiyta.
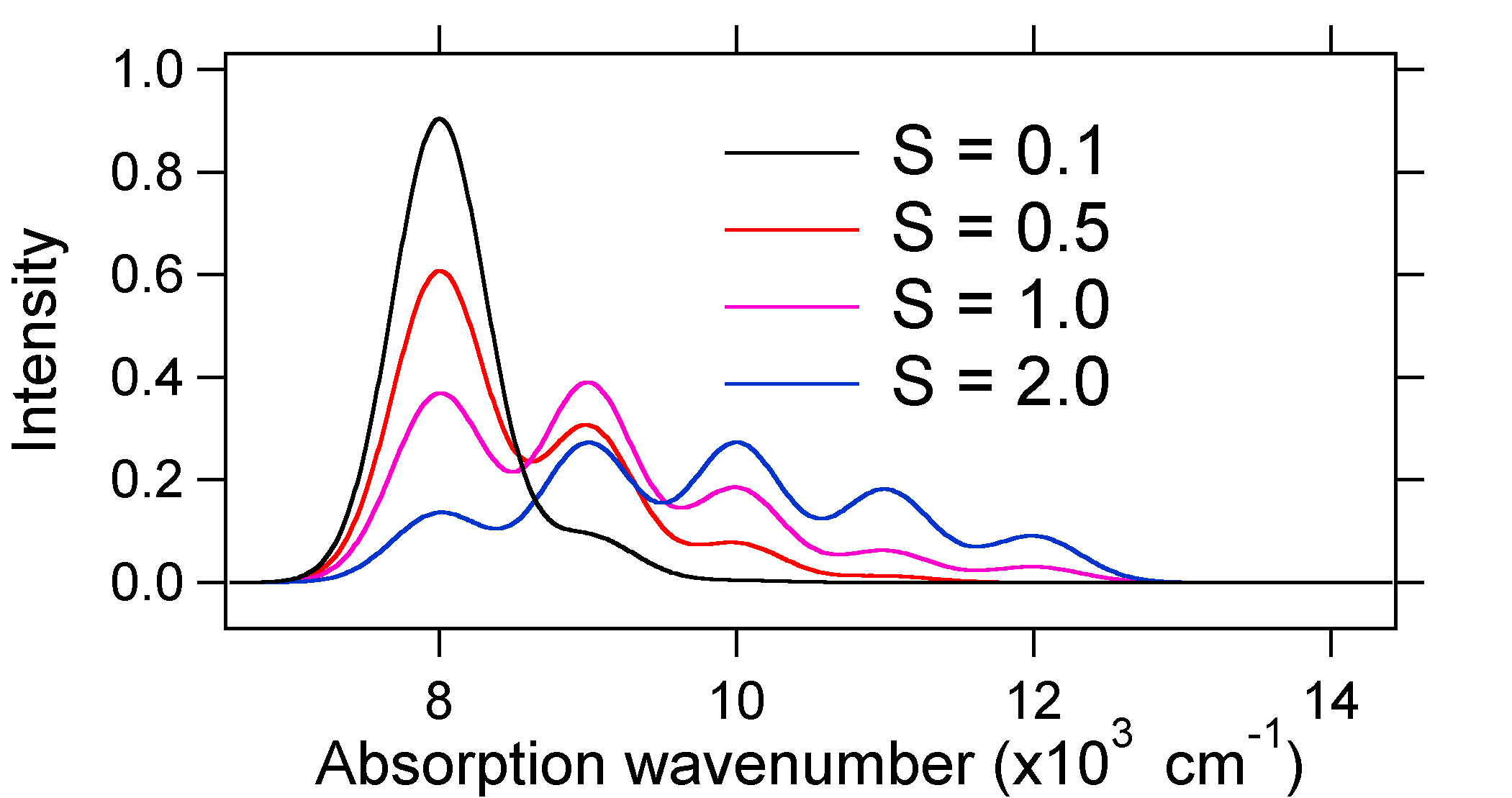
så naturen hos de relativa vibroniska bandintensiteterna kan berätta om det finns en förskjutning av jämviktskärnkoordinaten som åtföljde en övergång. När kommer det att öka bindningslängden (dvs \(Q_e > R_e\))? Detta inträffar när en elektron främjas från en bindningsmolekylär orbital till en icke-bindande eller antibindande molekylära orbitaler (dvs när bindningsordningen är mindre i exciterat tillstånd än marktillståndet).
- icke-bindande molekylär orbital \(\rightarrow\) bindning molekylär orbital
- Anti-bonding molekylär orbital \(\rightarrow\) bindning molekylär orbital
- Anti-bonding molekylär orbital \(\rightarrow\) icke-bindande molekylär orbital
kort sagt, när bindningsordningen är lägre i exciterat tillstånd än i marktillståndet, då \(Q_e> r_e\); en ökning av bindningslängden kommer att inträffa när detta händer.
- J. M. Luis, D. M. biskop, B. Kirtman. En annan metod för beräkning av Franck-Condon faktorer inklusive anharmonicitet. J. Chem. Phys., 120 (2004), s.813-822.
- Atkins, Peter och Julio de Paula. Fysikalisk kemi för biovetenskap. 2006. New York, NY: W. H. Freeman och företag. s. 563-564
- Franck-Condon princip. 1996, 68, 2243. IUPAC kompendium för kemisk terminologi 2: a upplagan (1997). www.iupac.org/goldbook/F02510.pdf
- E. Rabinowitch och Govindjee. Ljusabsorption och öde av Excitation av energi. 1969. Franck-Condon-Principen. http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
bidragsgivare
- Matthews Zi Ziering
-
Stefan Franzen (North Carolina State University)