
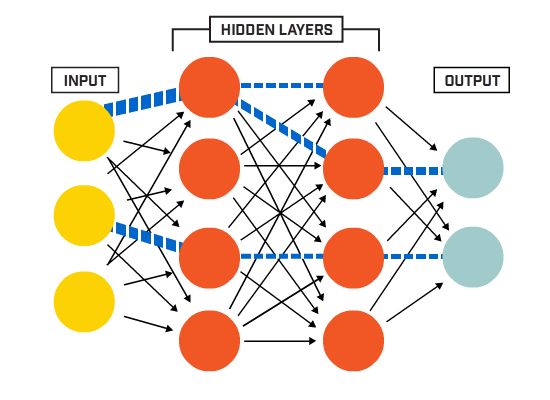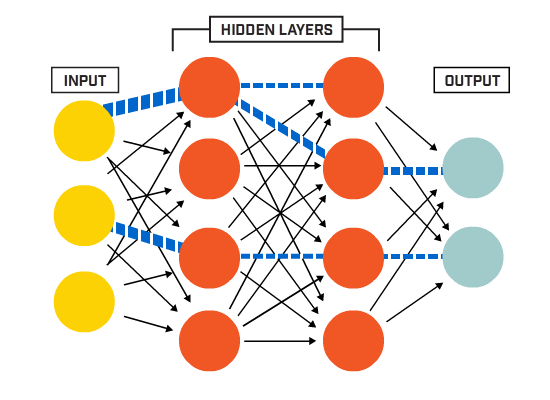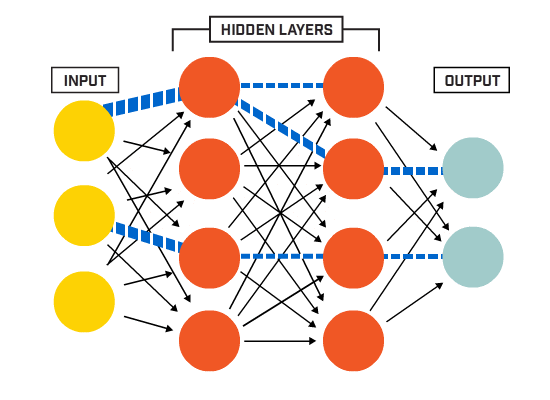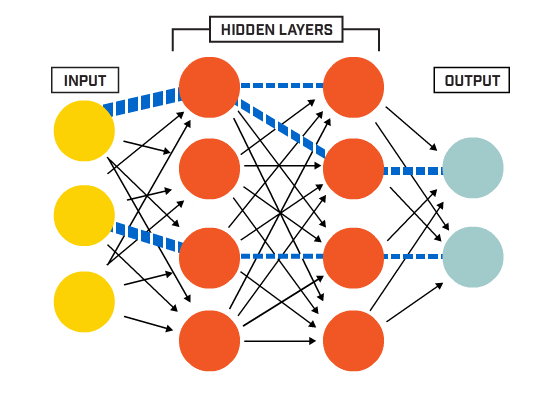
ett artificiellt neuralt nätverk (ann) är tillverkat av många sammankopplade neuroner:
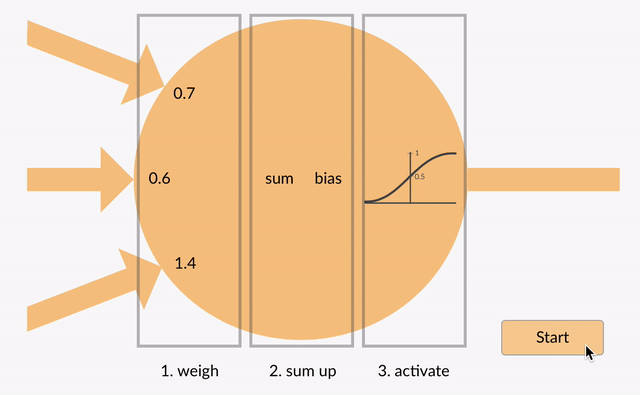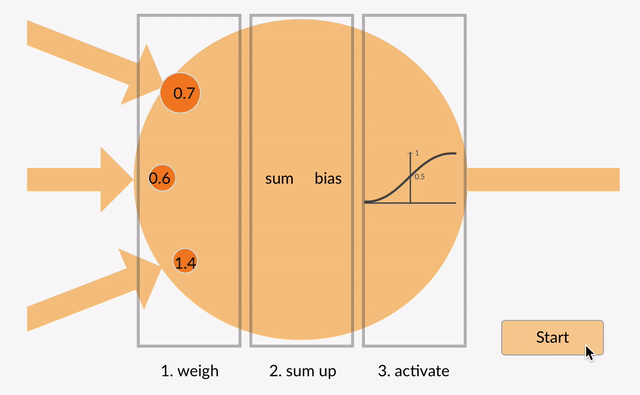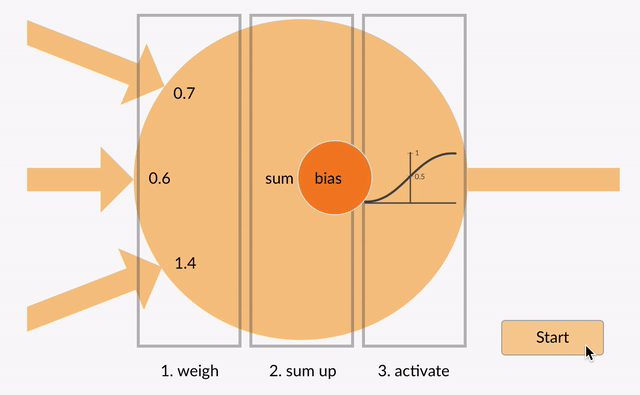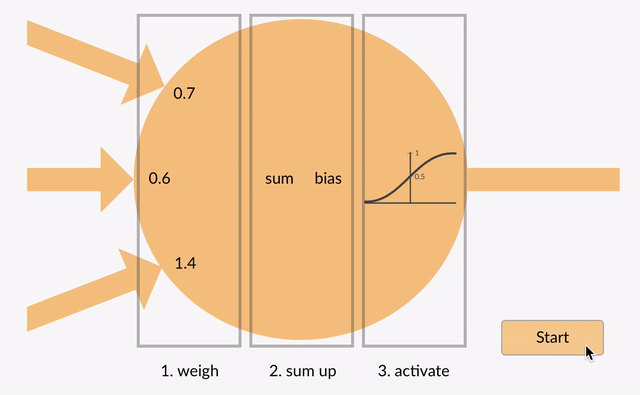
varje neuron tar in några flyttal (t.ex. 1.0, 0.5, -1.0) och multiplicerar dem med några andra flyttal (t. ex. 0,7, 0,6, 1,4) kända som vikter (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Vikterna fungerar som en mekanism för att fokusera på eller ignorera vissa ingångar.

vikter fungerar som mjuka grindar för att ignorera vissa funktioner (0) och fokusera på andra (+1) eller till och med hämma dem (-1)
de viktade ingångarna summeras sedan tillsammans (t. ex. 0.7 + 0.3 + -1.4 = -0.4) tillsammans med ett biasvärde (t.ex. -0.4 + -0.1 = -0.5).
det summerade värdet (x) omvandlas nu till ett utgångsvärde (y) enligt neurons aktiveringsfunktion(y = f (x)). Några populära aktiveringsfunktioner visas nedan:

t.ex. -0.5 om vi använder den läckande rektifierade linjära enheten (läckande Relu) aktiveringsfunktion: y = F(X) = F(-0.5) = max(0.1*-0.5, -0.5) = Max(-0.05, -0.5) = -0.05
neuronens utgångsvärde (t.ex. -0.05) är ofta en ingång för en annan neuron.
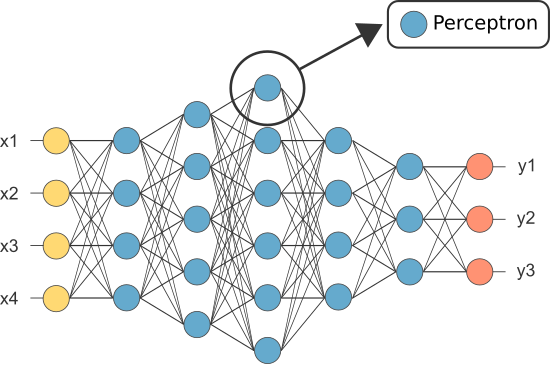
en av de första anns var dock känd som perceptronen och den bestod av av endast en enda neuron.

utgången från perceptronens (enda) neuron fungerar som den slutliga förutsägelsen.

låter koda vår egen Perceptron:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(Obs: vi har inte inkluderat någon inlärningsalgoritm i vårt exempel ovan — vi ska täcka inlärningsalgoritmer i en annan handledning)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

så varför behöver vi så många neuroner i en ANN om någon kommer att räcka (som klassificerare)?

tyvärr kan enskilda neuroner bara klassificera linjärt separerbara data.

men genom att kombinera neuroner tillsammans kombinerar vi i huvudsak deras beslutsgränser. Därför kan en ANN som består av många neuroner lära sig komplexa, icke-linjära beslutsgränser.

neuroner är kopplade ihop enligt en specifik nätverksarkitektur. Även om det finns olika arkitekturer, innehåller nästan alla lager. (OBS: Neuroner i samma lager ansluter inte till varandra)
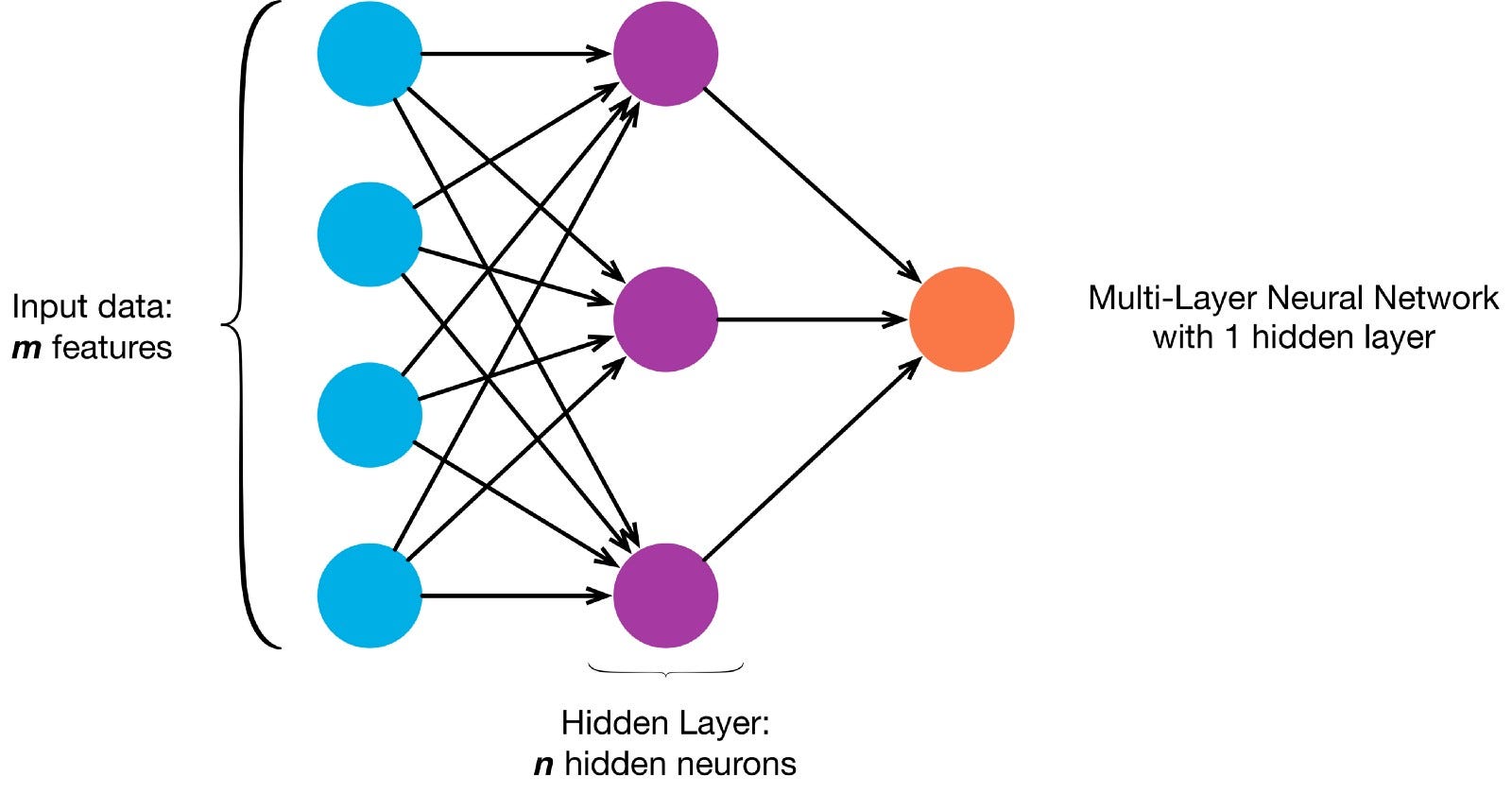
det finns vanligtvis ett ingångslager (innehållande ett antal neuroner ett utgångsskikt (innehållande ett antal neuroner lika med antalet klasser) och ett dolt lager (innehållande valfritt antal neuroner).

nät med mer än ett dolt lager anses vara ett djupt neuralt nät).
Låt oss bygga en djup NN för att måla den här bilden:

låter ladda ner bilden och ladda sina pixlar i en array
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
nu lär vi vår Ann att måla är en övervakad inlärningsuppgift, så vi måste skapa en märkt träningsuppsättning (våra träningsdata kommer att ha ingångar och förväntade utgångsetiketter för varje ingång). Träningsingångarna kommer att ha 2 värden (X,y-koordinaterna för varje pixel).
Med tanke på bildens enkelhet kan vi faktiskt närma oss detta problem på ett av två sätt. Ett klassificeringsproblem (där neurala nätet förutsäger om en pixel tillhör den” blå ”klassen eller den” grå ” klassen, med tanke på dess XY-koordinater) eller ett regressionsproblem (där neurala nätet förutsäger RGB-värden för en pixel med tanke på dess koordinater).
om du behandlar detta som ett regressionsproblem: träningsutgångarna kommer att ha 3 värden (de normaliserade R,g,b-värdena för varje pixel). – Låt oss använda den här metoden för nu.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
Nu kan vi skapa vår ANN:

- det ska ha 2 neuroner i ingångsskiktet (eftersom det finns 2 värden att ta in: x & Y — koordinater).
- Det ska ha 3 neuroner i utgångsskiktet (eftersom det finns 3 värden att lära sig: r, g, b).
- antalet dolda lager och antalet neuroner i varje dolt lager är två hyperparametrar att experimentera med (liksom antalet epoker vi kommer att träna det för, aktiveringsfunktionen etc) — jag använder 10 dolda lager med 100 neuroner i varje dolt lager (vilket gör detta till ett djupt neuralt nätverk)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
det utbildade nätverket kan nu förutsäga de normaliserade rgb-värdena för alla koordinater (t.ex. x, y = 1,1).
ann.predict(])
array(])
låter använda ANN för att förutsäga rgb — värdena för varje koordinat och låter visa de förutsagda rgb-värdena för hela bilden för att se hur bra det gjorde (kvalitativt-vi ska lämna utvärderingsmätningar för en annan handledning)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

försök ändra hyperparametrarna för att få bättre resultat.
om vi istället för att behandla detta som ett regressionsproblem behandlar vi detta som ett klassificeringsproblem, då kommer träningsutgångarna att ha 2 värden (sannolikheten för pixeln som tillhör var och en av de två klasserna: ”blå” och ”grå”)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
Vi kan bygga om vår ANN som en binär klassificerare med 2 neuroner i ingångsskiktet, 2 neuroner i utgångsskiktet och 100 neuroner i det dolda lagret (med 10 dolda lager)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
Vi kan nu använda den utbildade ann för att förutsäga klassen som varje pixel tillhör (0: ”grå” eller 1: ”Blå”). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: ”grey”)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

