Förstå Deep Rest Networks

Deep rest networks (ResNet) tog den djupa inlärningsvärlden med storm när Microsoft Research släppte Deep Rest Learning för bildigenkänning. Dessa nätverk ledde till 1: a plats vinnande poster i alla fem huvudspåren i ImageNet och COCO 2015-tävlingarna, som täckte bildklassificering, objektdetektering och semantisk segmentering. Resnets robusthet har sedan dess bevisats av olika visuella igenkänningsuppgifter och av icke-visuella uppgifter som involverar tal och språk. Jag använde också ResNet utöver andra djupinlärningsmodeller i min doktorsavhandling.

detta inlägg kommer att sammanfatta de tre papper nedan, som alla är skrivna eller samskrivna av Resnets uppfinnare Kaiming He, för jag tror att originalpapper ger den mest intuitiva och detaljerade förklaringen av modellen/nätverket. Förhoppningsvis kan det här inlägget hjälpa dig att få en bättre förståelse för kärnan i återstående nätverk.

• Deep Rest Learning för bildigenkänning
• identitetskort i Deep rest Networks
• aggregerad Resttransformation för Deep Neural Networks

Intuition på Deep Rest Network (stackoverflow ref)

ett restblock visas som följande:

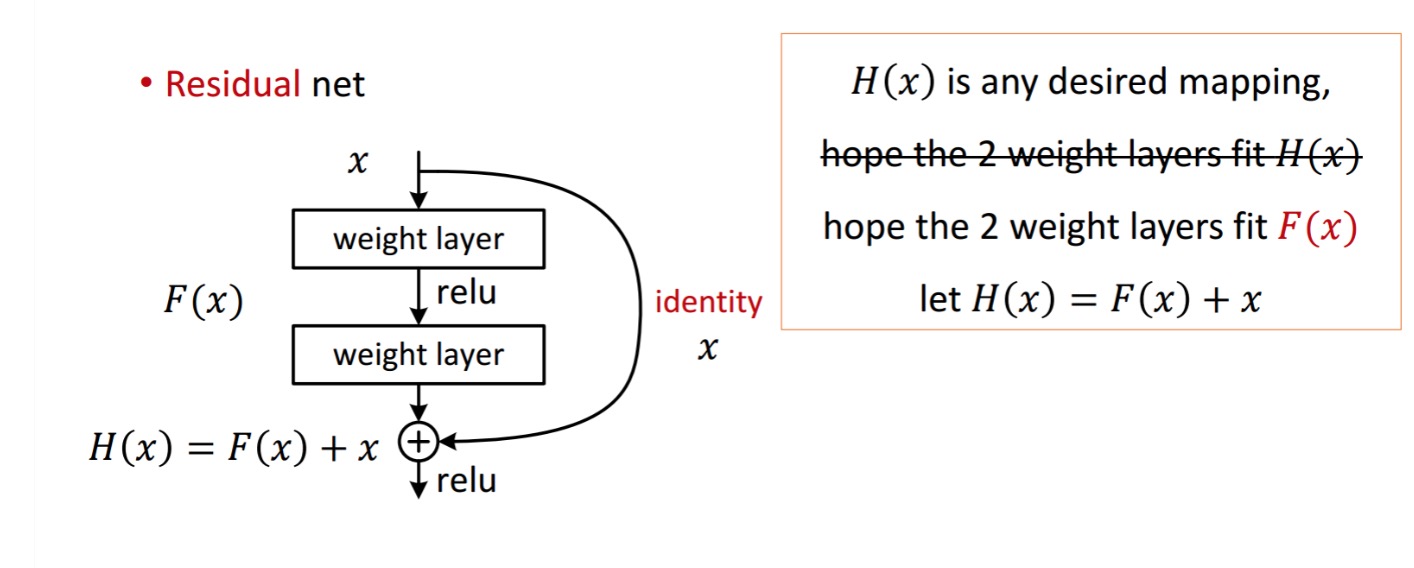
så den återstående enheten som visas erhålls genom bearbetning med två viktlager. Sedan lägger till för att erhålla . Antag nu att det är din ideala förutspådda produktion som matchar din mark sanning. Eftersom att få det önskade beror på att få det perfekta . Det betyder att de två viktlagren i restenheten faktiskt borde kunna producera det önskade , då blir idealet garanterat.

erhålls från följande.

erhålls från följande.

författarna antar att den återstående kartläggningen (dvs. ) kan vara lättare att optimera än . För att illustrera med ett enkelt exempel, anta att idealet . Då för en direkt kartläggning skulle det vara svårt att lära sig en identitetskartläggning eftersom det finns en stapel icke-linjära lager enligt följande.

så att approximera identitetskartläggningen med alla dessa vikter och ReLUs i mitten skulle vara svårt.

Nu, om vi definierar önskad kartläggning, behöver vi bara få enligt följande.

att uppnå ovanstående är lätt. Ställ bara in någon vikt till noll så får du en nollutgång. Lägg tillbaka och du får önskad kartläggning.

djup återstående inlärning för bildigenkänning

Problem

När djupare nätverk börjar konvergera har ett nedbrytningsproblem exponerats: när nätverksdjupet ökar blir noggrannheten mättad och försämras sedan snabbt.

se förnedrande i aktion:

Låt oss ta ett grunt nätverk och dess djupare motsvarighet genom att lägga till fler lager i det.

Worst case scenario: Deeper-modellens tidiga lager kan ersättas med grunt nätverk och de återstående lagren kan bara fungera som en identitetsfunktion (ingång lika med utgång).

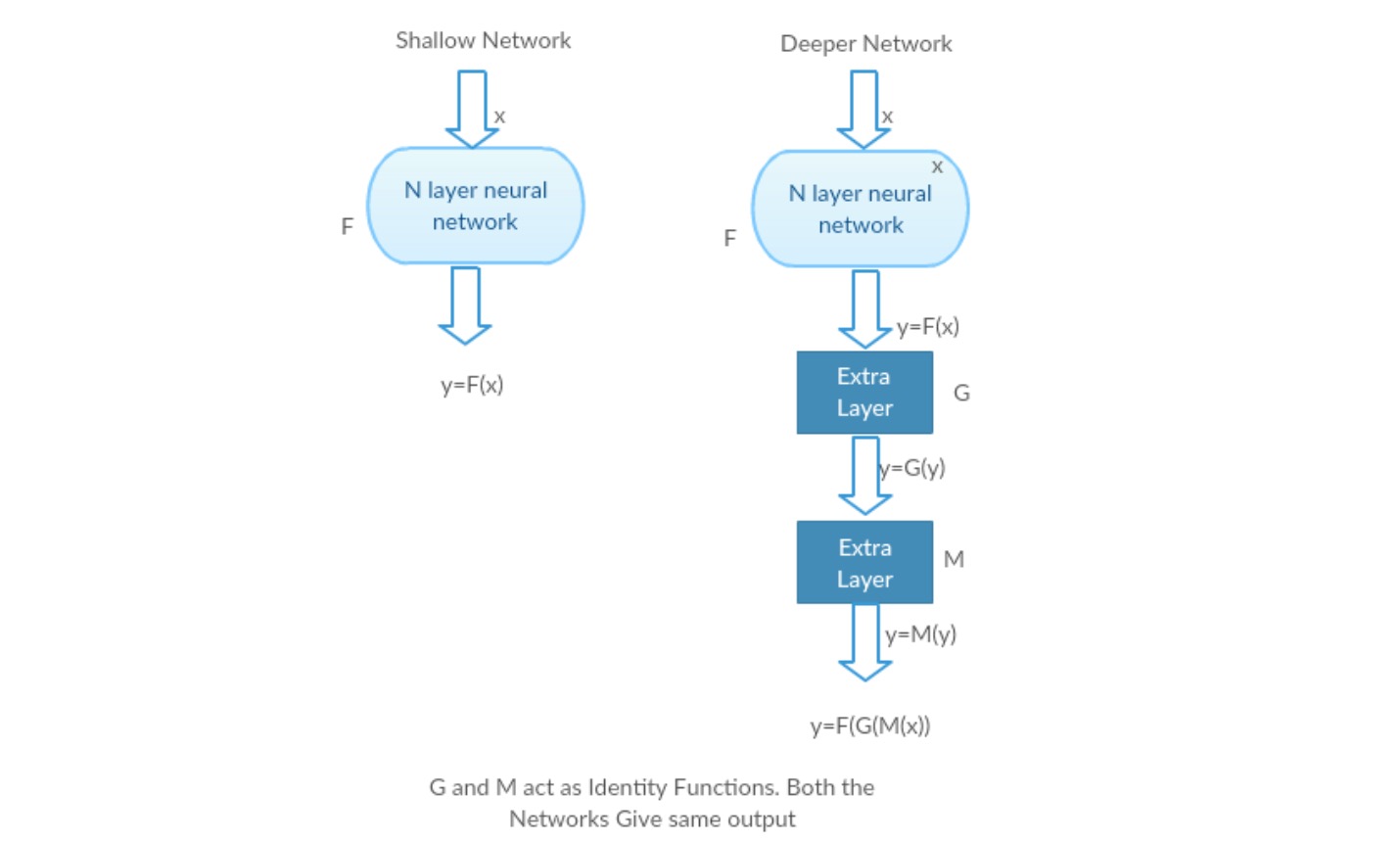
givande scenario: i det djupare nätverket approximerar de ytterligare lagren bättre kartläggningen än den är grundare motdel och minskar felet med en betydande marginal.

Experiment: I värsta fall bör både det grunda nätverket och den djupare varianten av det ge samma noggrannhet. I det givande scenariot bör den djupare modellen ge bättre noggrannhet än den är grundare motdel. Men experiment med våra nuvarande lösare avslöjar att djupare modeller inte fungerar bra. Så att använda djupare nätverk försämrar modellens prestanda. Dessa papper försöker lösa detta problem med hjälp av Deep Rest learning framework.

hur man löser?

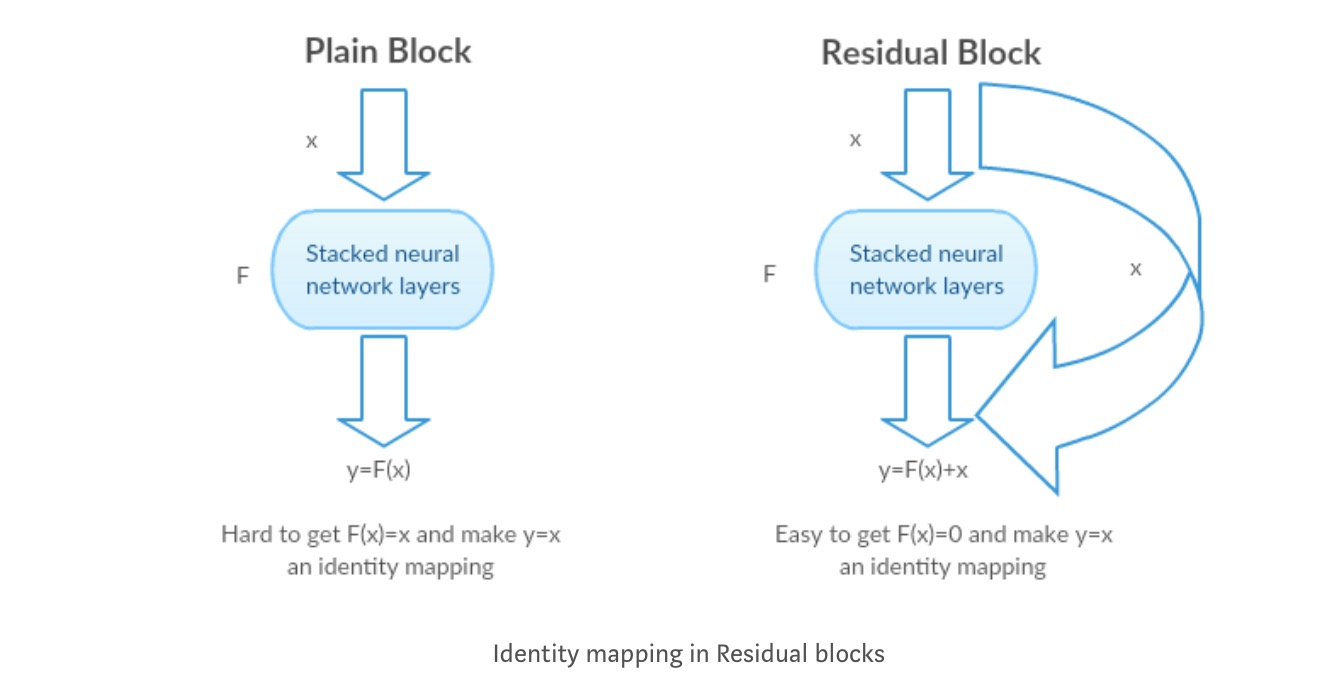
istället för att lära sig en direkt kartläggning av med en funktion (några staplade icke-linjära lager). Låt oss definiera restfunktionen med , som kan omformas till , var och representerar de staplade icke-linjära skikten och identitetsfunktionen(input=output) respektive.

författarens hypotes är att det är lätt att optimera den kvarvarande kartläggningsfunktionen än att optimera den ursprungliga, orefererade kartläggningen .

Intuition bakom Restblock:

Låt oss ta identitetskartläggningen som ett exempel (t.ex.). Om identitetskartläggningen är optimal kan vi enkelt trycka resterna till noll () än att passa en identitetskartläggning () med en stapel icke-linjära lager. På ett enkelt språk är det väldigt lätt att komma fram till en lösning som snarare än att använda stack av icke-linjära cnn-lager som funktion (Tänk på det). Så, den här funktionen är vad författarna kallade Restfunktion.

författarna gjorde flera tester för att testa sin hypotes. Låt oss titta på var och en av dem nu.

testfall:

ta ett vanligt nätverk (vgg kind 18 layer network) (Network-1) och en djupare variant av det (34-lager, nätverk-2) och Lägg till kvarvarande lager i nätverket-2 (34 lager med återstående anslutningar, nätverk-3).

designa nätverket:

1. Använd 3 * 3 Filter mestadels.
2. nedprovtagning med CNN-lager med steg 2.
3. Global average pooling layer och ett 1000-vägs helt anslutet lager med Softmax i slutet.

det finns två typer av återstående anslutningar:

I. identitetsgenvägarna () kan användas direkt när ingången () och utgången () har samma dimensioner.

II. när dimensionerna ändras, a) genvägen utför fortfarande identitetskartläggning, med extra nollposter vadderade med den ökade dimensionen. B) projektionsgenvägen används för att matcha dimensionen (gjord av 1*1 conv) med följande formel

resultat

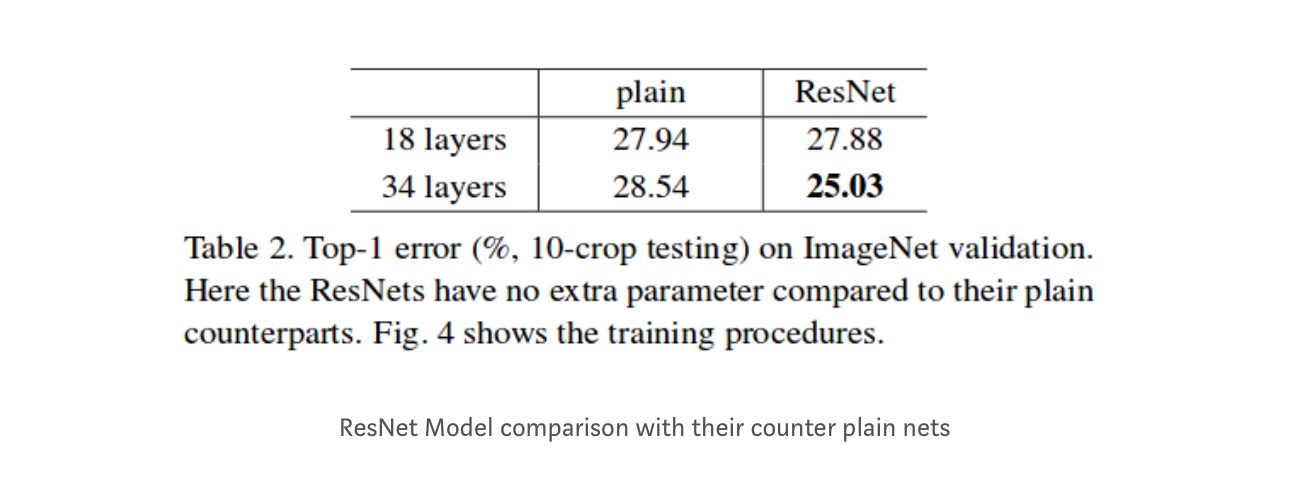
Även om 18-lagernätverket bara är delrummet i 34-lagernätverket, fungerar det fortfarande bättre. ResNet överträffar med en signifikant marginal om nätverket är djupare

djupare studier

dessutom studeras fler nätverk:

varje ResNet-block är antingen 2 lager djupt (används i små nätverk som resnet 18, 34) eller 3 lager djup( resnet 50, 101, 152).

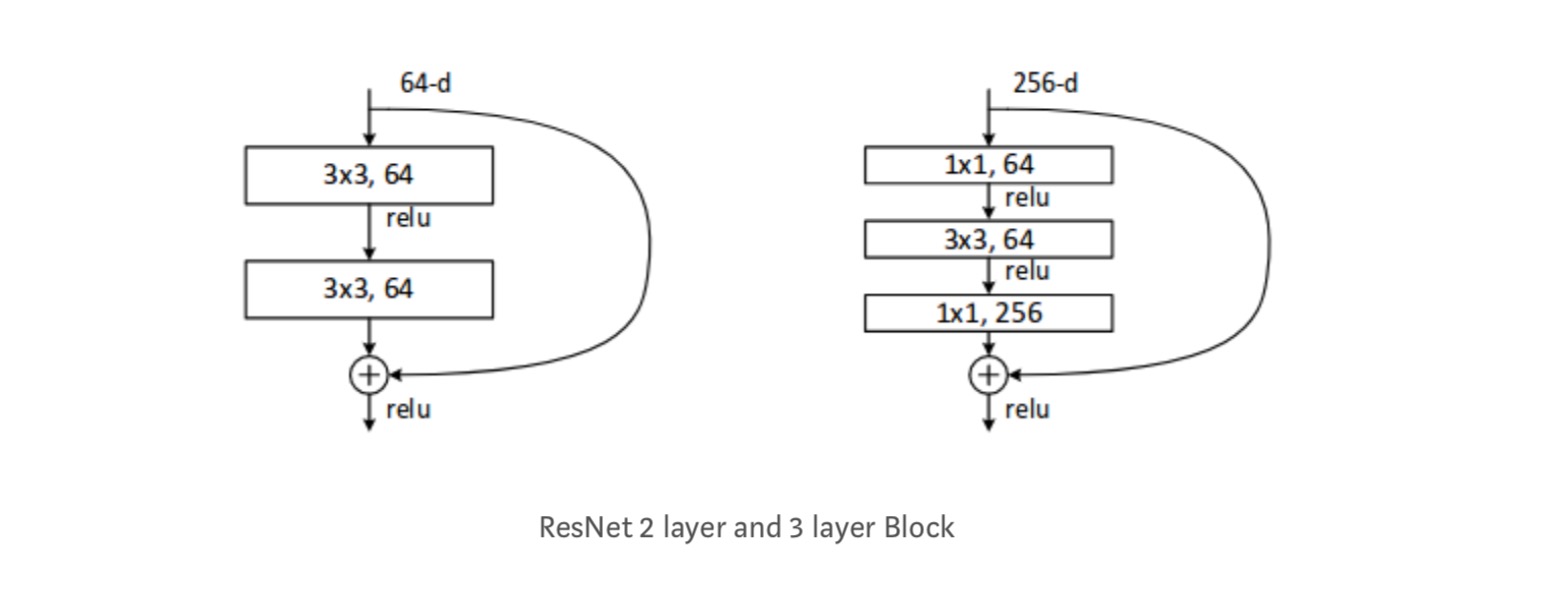
observationer

1. ResNet-nätverk konvergerar snabbare jämfört med vanlig motdel av det.
2. identitet vs projektion shorcuts. Mycket små inkrementella vinster med hjälp av projektionsgenvägar (ekvation-2) i alla lager. Så alla ResNet-block använder bara identitetsgenvägar med Projektionsgenvägar som endast används när dimensionerna ändras.
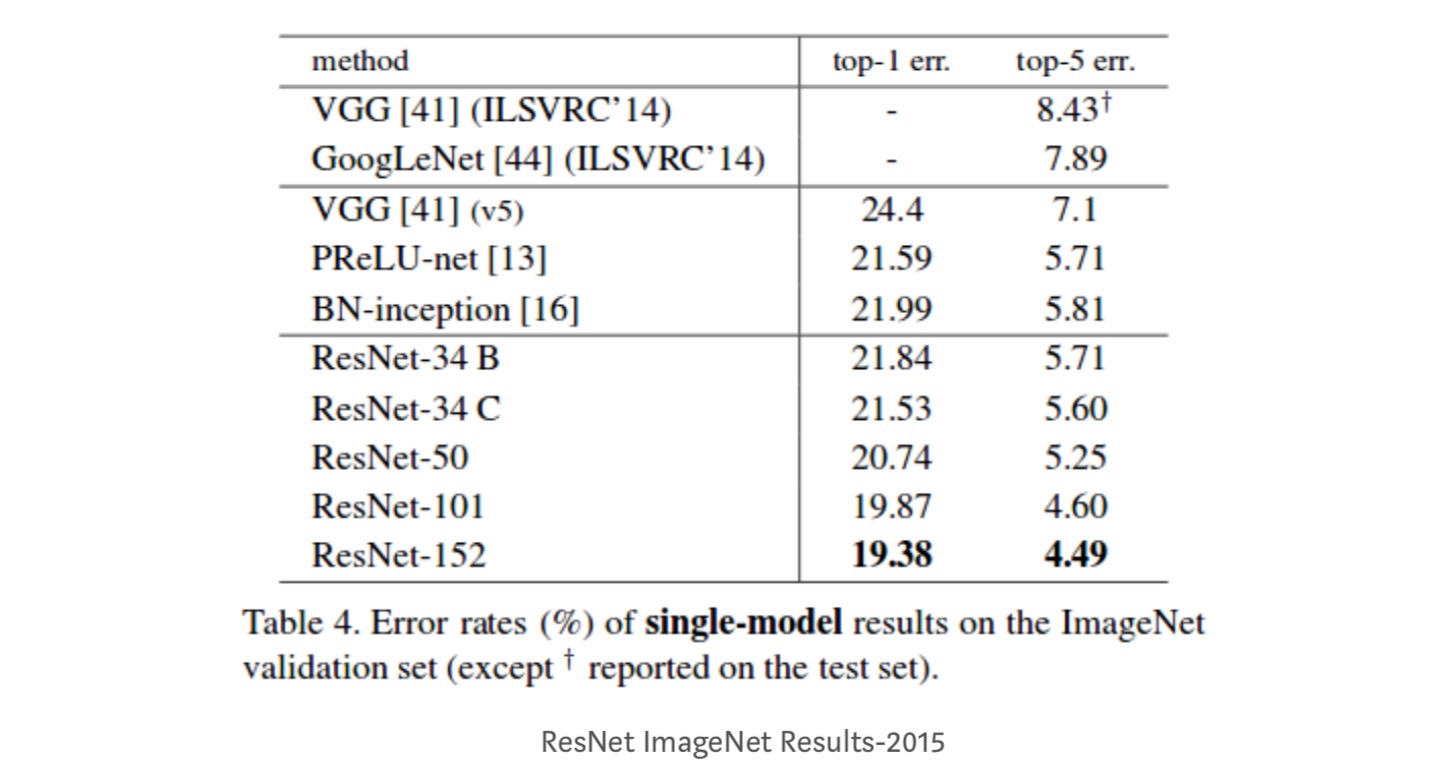
3. ResNet – 34 uppnådde ett top-5-valideringsfel på 5.71% bättre än BN-inception och VGG. ResNet – 152 uppnår ett top-5-valideringsfel på 4,49%. En ensemble med 6 modeller med olika djup uppnår ett top-5-valideringsfel på 3, 57%. Vinna 1: a plats i ILSVRC-2015

Identity mappings in Deep rest Networks

denna uppsats ger teoretisk förståelse för varför försvinnande gradientproblem inte finns i Restnätverk och rollen för hoppa över anslutningar (hoppa över anslutningar betyder ingången eller ) genom att ersätta Identitetskartläggning (x) med olika funktioner.

Inledning

djupa restnät består av många staplade ”Restenheter”. Varje enhet kan uttryckas i en allmän form:

där och är input och output av enheten, och är en restfunktion. I den sista papper, är en identitetskartläggning och är en ReLU funktion.

den centrala tanken med ResNets är att lära sig additiv restfunktion med avseende på, med ett nyckelval att använda en identitetskartläggning . Detta realiseras genom att bifoga en identitetshoppanslutning (”genväg”).

i detta dokument analyserar vi djupa kvarvarande nätverk genom att fokusera på att skapa en ”direkt” väg för att sprida information — inte bara inom en återstående enhet utan genom hela nätverket. Våra härledningar avslöjar att om båda och är identitetsmappningar, kan signalen direkt spridas från en enhet till andra enheter, både framåt och bakåt. Våra experiment visar empiriskt att träning i allmänhet blir lättare när arkitekturen är närmare ovanstående två förhållanden.

för att förstå rollen som hoppa över anslutningar analyserar och jämför vi olika typer av . Vi finner att identitetskartläggningen som valts i det senaste papperet uppnår den snabbaste felminskningen och lägsta träningsförlusten bland alla varianter som vi undersökte, medan hoppa över anslutningar av skalning, gating och 1 2CB 1-svängningar leder alla till högre träningsförlust och fel. Dessa experiment tyder på att det är bra att hålla en ”ren” informationsväg för att underlätta optimeringen.

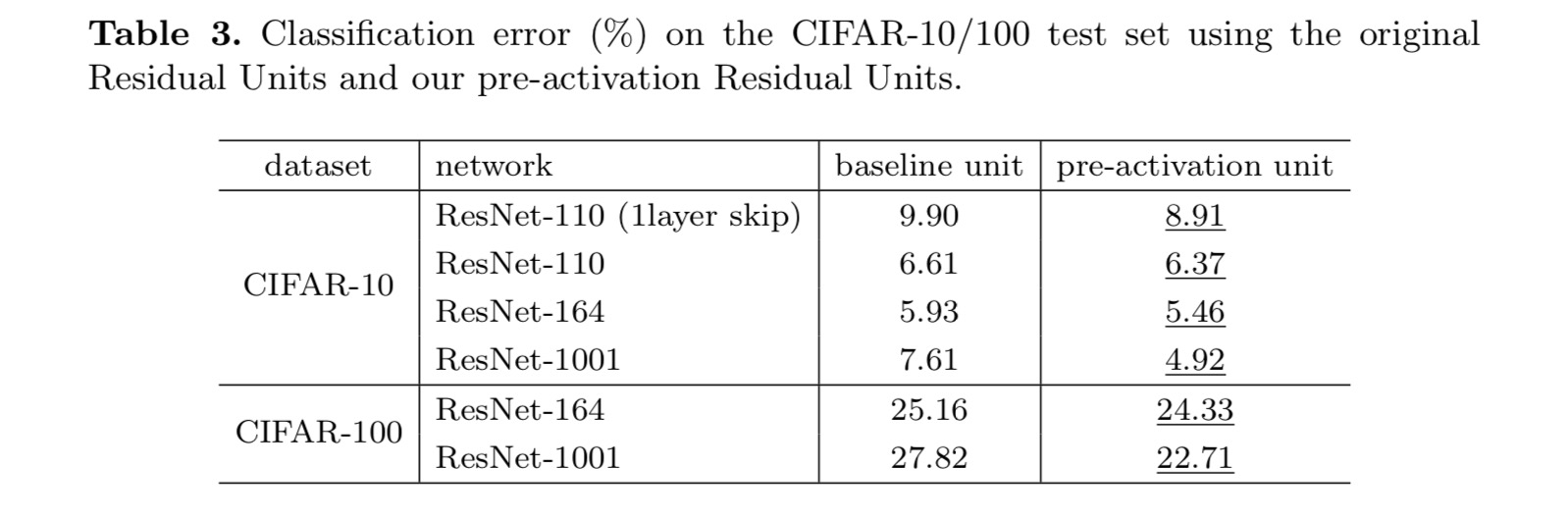
för att konstruera en identitetskartläggning ser vi aktiveringsfunktionerna (ReLU och BN) som ”föraktivering” av viktskikten, i motsats till konventionell visdom av ”postaktivering”. Denna synvinkel leder till en ny residualenhetsdesign, som visas i följande figur. Baserat på denna enhet presenterar vi konkurrenskraftiga resultat på CIFAR-10/100 med ett 1001-lagers ResNet, vilket är mycket lättare att träna och generaliserar bättre än det ursprungliga ResNet. Vi rapporterar vidare förbättrade resultat på ImageNet med ett 200-lagers ResNet, för vilket motsvarigheten till det sista papperet börjar överpassa. Dessa resultat tyder på att det finns mycket utrymme att utnyttja dimensionen av nätverksdjup, en nyckel till framgången för modern djupinlärning.

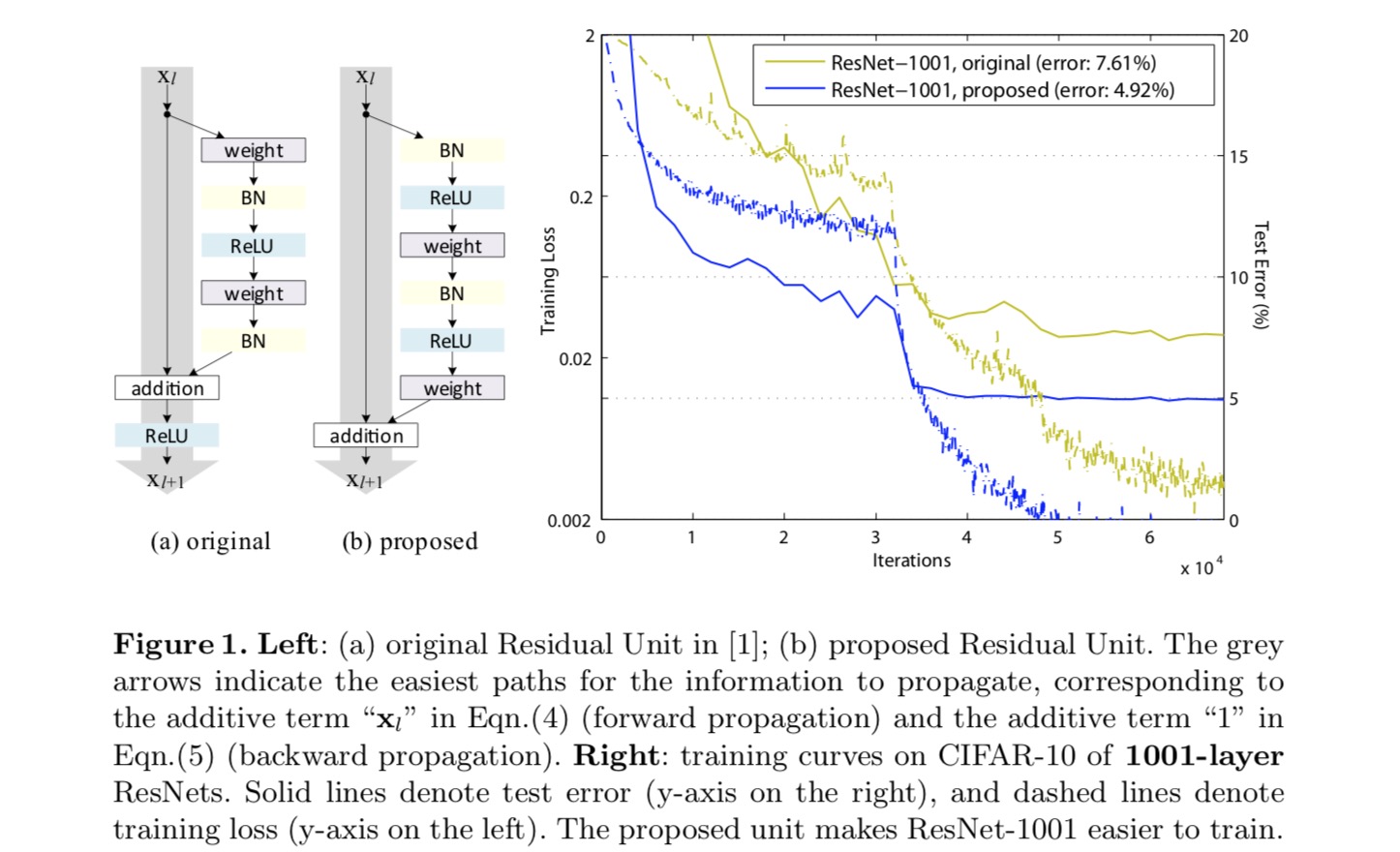
analys av djupa kvarvarande nätverk

Resnät som utvecklats i det senaste papperet är modulariserade arkitekturer som staplar byggstenar med samma anslutningsform. I detta papper kallar vi dessa block”återstående enheter”. Den ursprungliga Restenheten i det sista papperet utför följande beräkning:

Här är inmatningsfunktionen till den-TH Restenheten. är en uppsättning av vikter ( och fördomar) i samband med-Th Restenhet, och är antalet lager i en Restenhet (är 2 eller 3 i den sista papper). betecknar restfunktionen, e.g., en stapel med två 3 2CB 3 faltningslager i det sista papperet. Funktionen är operationen efter elementvis tillsats, och i det sista papperet är ReLU. Funktionen är inställd som en identitetskartläggning: .

om är också en identitetskartläggning:, vi kan få:

rekursivt vi kommer att ha:

för någon djupare enhet och någon grundare enhet . Denna ekvation uppvisar några trevligaegenskaper. (1) funktionen hos någon djupare enhet kan representeras som funktionen hos någon grundare enhet plus en restfunktion i en form av , vilket indikerar att modellen är i en rest mode mellan alla enheter och . (2) funktionen för varje djup enhet är summan av utgångarna från alla föregående restfunktioner (plus). Detta står i kontrast till ett ”vanligt nätverk” där en funktion är en serie matrisvektorprodukter, säger (ignorerar BN och ReLU).

ovanstående ekvation leder också till fina bakåtutbredningsegenskaper. Betecknar förlustfunktionen som, från kedjeregeln för backpropagation har vi:

ovanstående ekvation indikerar att gradienten kan sönderdelas i två additiva termer: en term som sprider information direkt utan att det rör sig om några viktlager, och en annan term som sprider sig genom viktlagren. Tillsatsperioden för säkerställer att informationen direkt sprids tillbaka till någon grundare enhet l. ovanstående ekvation antyder också att det är osannolikt att lutningen avbryts för en mini-sats, eftersom termen i allmänhet inte alltid kan vara -1 för alla prover i en mini-sats. Detta innebär att gradienten av ett lager Inte försvinner även när vikterna är godtyckligt små.

ovanstående två ekvationer antyder att signalen kan spridas direkt från vilken enhet som helst till en annan, både framåt och bakåt. Grunden för de första ovanstående två ekvationerna är två identitetsmappningar: (1) identitetshoppanslutningen och (2) villkoret som är en identitetskartläggning.

betydelsen av identity skip connections

låt oss överväga en enkel modifiering, , för att bryta identitetsgenvägen:

Var är en modulerande skalär (för enkelhetens skull antar vi fortfarande är identitet). Rekursivt tillämpa denna formulering får vi en ekvation som liknar den ovan:

där notationen absorberar skalärerna i restfunktionerna. På samma sätt har vi backpropagation av följande form:

Till skillnad från den tidigare ekvationen, i denna ekvation moduleras den första additiva termen med en faktor . För ett extremt djupt nätverk( är stort), om för alla kan denna faktor vara exponentiellt stor; om för alla kan denna faktor vara exponentiellt liten och försvinna , vilket blockerar den backpropagerade signalen från genvägen och tvingar den att strömma genom viktlagren. Detta resulterar i optimeringsproblem som vi visar genom experiment.

i ovanstående analys ersätts den ursprungliga identity skip-anslutningen med en enkel skalning . Om skip-anslutningen representerar mer komplicerade transformationer (såsom grinding och 1-1-omvälvningar), i ovanstående ekvation blir den första termen var är derivatet av . Denna produkt kan också hindra informationsförökning och hindra träningsförfarandet som bevittnat i följande experiment.

experiment på hoppa över anslutningar

vi experimenterar med 110-lagers ResNet på CIFAR-10. Denna extremt djupa ResNet – 110 har 54 Tvåskiktsrestenheter (bestående av 3 3-veckningslager i 3-skikt) och är utmanande för optimering. Olika typer av hoppanslutningar experimenteras. Se följande figur:

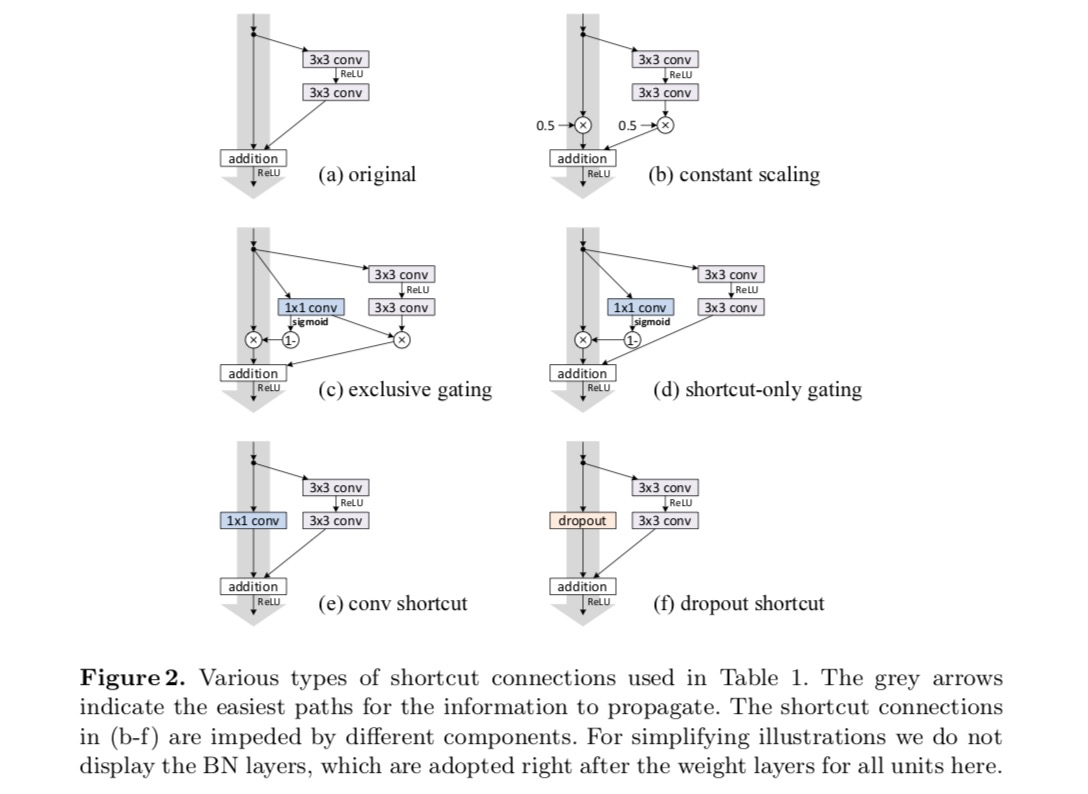
klassificeringsresultaten visas i följande tabell:

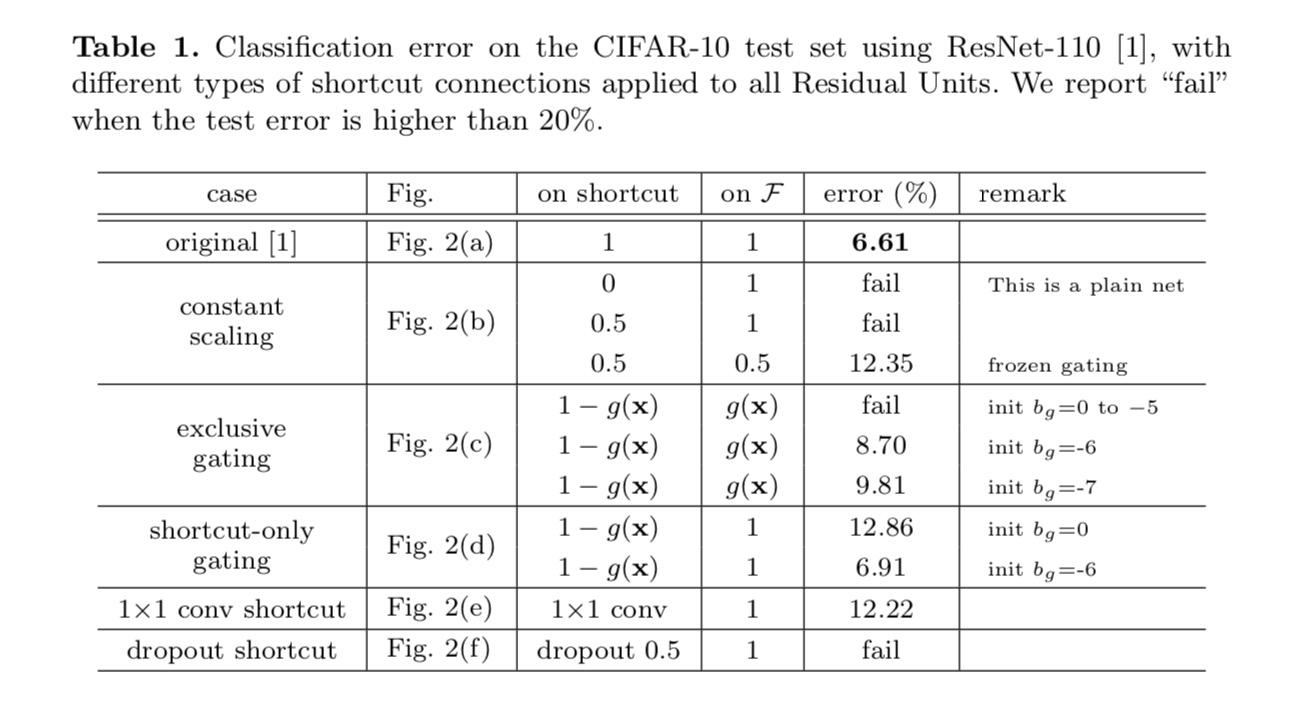
som indikeras av de grå pilarna i ovanstående figur är genvägsanslutningarna de mest direkta sökvägarna för informationen att sprida. Multiplikativa manipulationer (skalning, gating, 1-1-svängningar och bortfall) på genvägarna kan hämma informationsutbredning och leda till optimeringsproblem.

det är anmärkningsvärt att gating och 1 1 1 faltningsgenvägar införa fler parametrar, och bör ha starkare representations förmågor än identitetsgenvägar. I själva verket täcker genvägsgrinden och 1 2CB 1-faltningen lösningsutrymmet för identitetsgenvägar (dvs. de kan optimeras som identitetsgenvägar). Men deras träningsfel är högre än för identitetsgenvägar, vilket indikerar att nedbrytningen av dessa modeller orsakas av optimeringsproblem istället för representativa förmågor.

användning av Aktiveringsfunktioner

experiment i ovanstående avsnitt antas att eftertillsatsaktiveringen är identitetskartläggningen. Men i ovanstående experiment är ReLU som utformad i det första papperet. Därefter undersöker vi effekterna av .

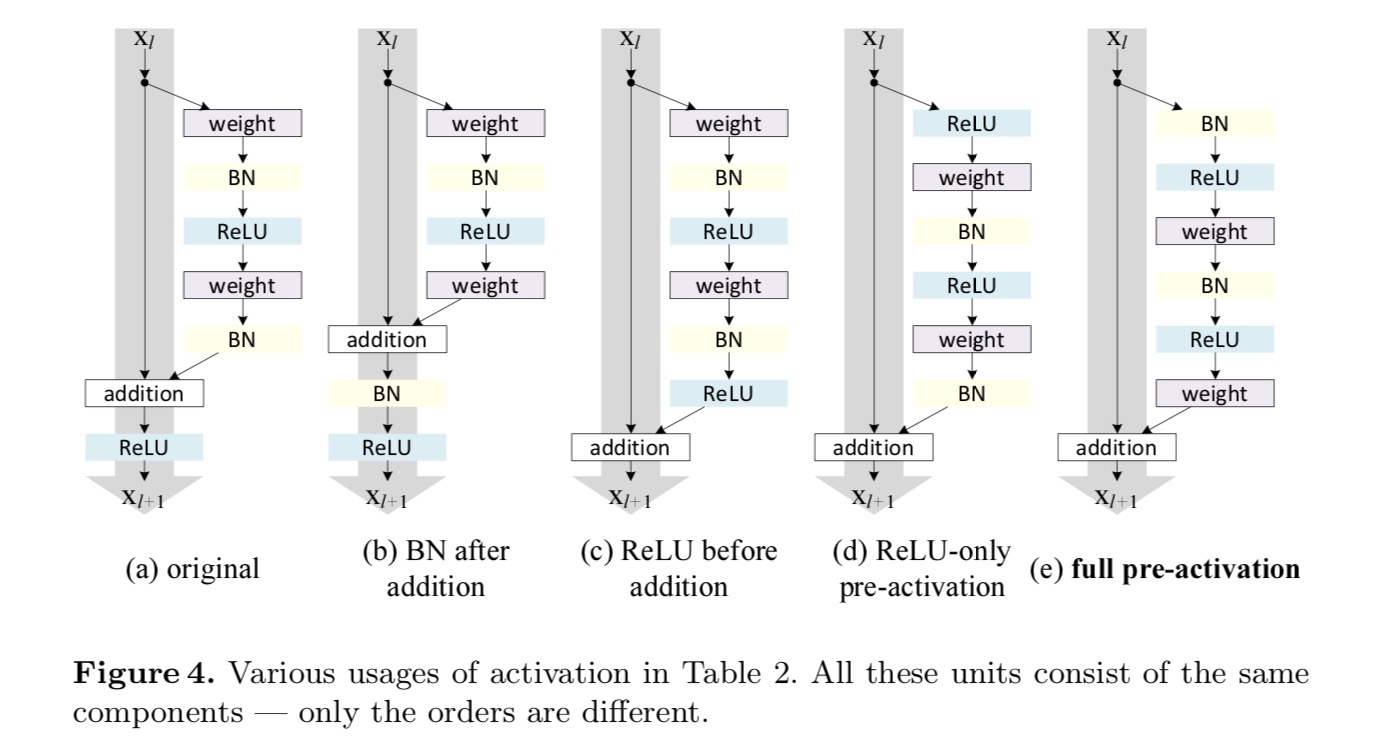
vi vill göra en identitetskartläggning, som görs genom att omorganisera aktiveringsfunktionerna (ReLU och/eller BN, batchnormalisering). I följande figur har den ursprungliga Restenheten i det sista papperet en form i Fig. 4 (a) – BN används efter varje viktlager, och ReLU antas efter BN förutom att den sista ReLU i en Restenhet är efter elementvis tillsats ( = ReLU). Fig. 4 (b-e) visa de alternativ vi undersökte.

experiment på aktivering

i det här avsnittet experimenterar vi med ResNet-110 och en 164-lagers Flaskhalsarkitektur (betecknad som ResNet-164). En flaskhalsrester består av ett lager på 1-1 1 för att minska dimensionen, ett lager på 3-3 och ett lager på 1-1 för att återställa dimensionen. Som utformad i den sista papper, är dess beräkningskomplexitet liknar de två-3 2CB 3 resterande enhet.

Efter aktivering eller föraktivering?

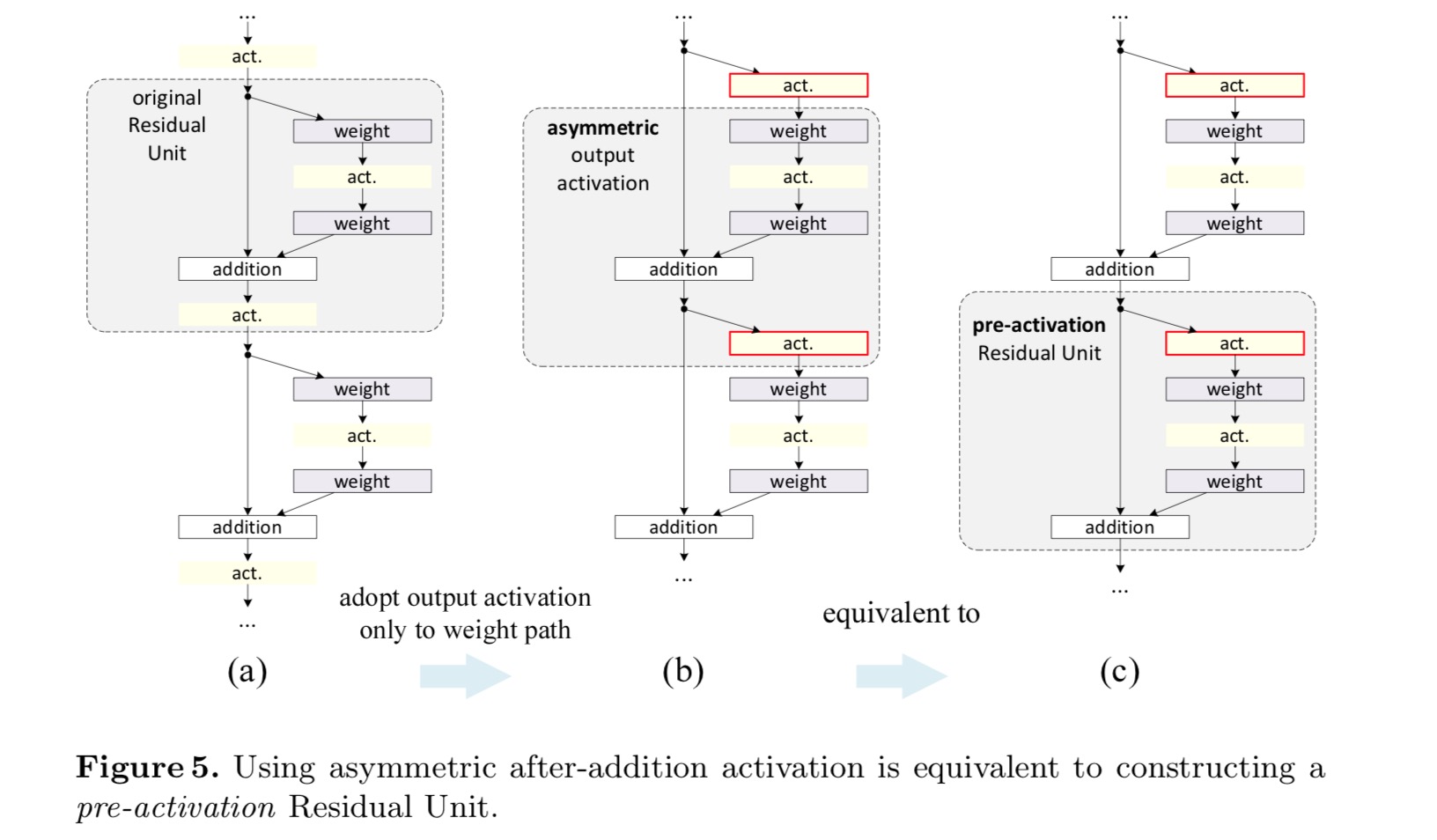
i den ursprungliga designen påverkar aktiveringen båda vägarna i nästa Restenhet: . Därefter utvecklar vi en asymmetrisk form där en aktivering endast påverkar sökvägen:, för någon . Genom att byta namn på notationerna har vi följande form:

för denna nya Restenhet som i ovanstående ekvation blir den nya eftertillsatsaktiveringen en identitetskartläggning. Denna design innebär att om en ny eftertillsatsaktivering är asymmetriskt antagen, motsvarar den omarbetning som föraktivering av nästa Restenhet. Detta illustreras i följande figur:

skillnaden mellan postaktivering/föraktivering orsakas av närvaron av det elementvisa tillägget. För ett vanligt nätverk som har N-lager finns det n – 1-aktiveringar (BN/ReLU), och det spelar ingen roll om vi tänker på dem som post-eller pre-aktiveringar. Men för grenade lager som slås samman genom tillägg är aktiveringspositionen viktig. De olika användningarna av aktivering visas i Figur 4.

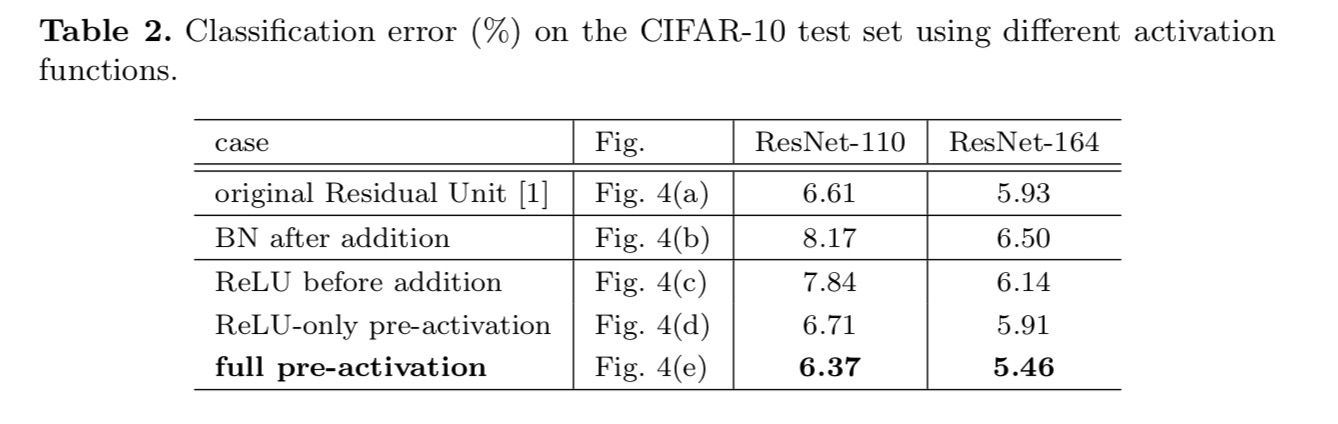
vi experimenterar med två sådana mönster: (1) ReLU-endast föraktivering och (2) full föraktivering där BN och ReLU båda antas före viktlager. På något sätt överraskande, när BN och ReLU båda används som föraktivering, förbättras resultaten med friska marginaler

vi finner att effekten av föraktivering är dubbelt. För det första underlättas optimeringen ytterligare (jämför med baslinjen ResNet) eftersom f är en identitetskartläggning. För det andra förbättrar användningen av BN som föraktivering regularisering av modellerna.

slutsats

denna uppsats undersöker utbredningsformuleringarna bakom anslutningsmekanismerna för djupa kvarvarande nätverk. Våra härledningar innebär att identitets genväg anslutningar och identitet efter tillsats aktivering är avgörande för att göra informationsutbredning smidig. Ablationsexperiment visar fenomen som överensstämmer med våra härledningar. Vi presenterar också 1000-lager djupa nätverk som lätt kan tränas och uppnå förbättrad noggrannhet.

aggregerad Resttransformation för djupa neurala nätverk

introduktion

forskning om visuell igenkänning genomgår en övergång från ”funktionsteknik” till ”nätverksteknik”. Mänsklig ansträngning har skiftats till att utforma bättre nätverksarkitekturer för inlärningsrepresentationer.

design av arkitekturer blir allt svårare med det växande antalet hyperparametrar, särskilt när det finns många lager. VGG-näten uppvisar en enkel men effektiv strategi för att bygga mycket djupa nätverk: stapla byggstenar av samma form. Denna strategi ärvs av ResNets som staplar moduler av samma topologi. Denna enkla regel minskar de fria valen av hyperparametrar, och djupet exponeras som en väsentlig dimension i neurala nätverk. Dessutom hävdar vi att enkelheten i denna regel kan minska risken för överanpassning av hyperparametrarna till en specifik dataset. Robustheten hos VGG-nät och Resnät har bevisats av olika visuella igenkänningsuppgifter och av icke-visuella uppgifter som involverar tal och språk.

Till skillnad från VGG-nets har familjen Inception-modeller visat att noggrant utformade topologier kan uppnå övertygande noggrannhet med låg teoretisk komplexitet. Startmodellerna har utvecklats över tiden, men en viktig gemensam egenskap är en split-transform-merge-strategi. I en Startmodul delas ingången upp i några lägre dimensionella inbäddningar (med 1 2 1 1 1 varv), transformerad av en uppsättning specialfilter (3 3 3 5 5 5, 5, etc.), och sammanfogas genom sammanfogning. Split-transform-merge-beteendet hos Startmoduler förväntas närma sig representationskraften hos stora och täta lager, men med en betydligt lägre beräkningskomplexitet.

trots god noggrannhet har förverkligandet av startmodeller åtföljts av en serie komplicerade faktorer. Även om noggranna kombinationer av dessa komponenter ger utmärkta neurala nätverksrecept är det i allmänhet oklart hur man anpassar Startarkitekturerna till nya dataset/uppgifter, särskilt när det finns många faktorer och hyperparametrar som ska utformas.

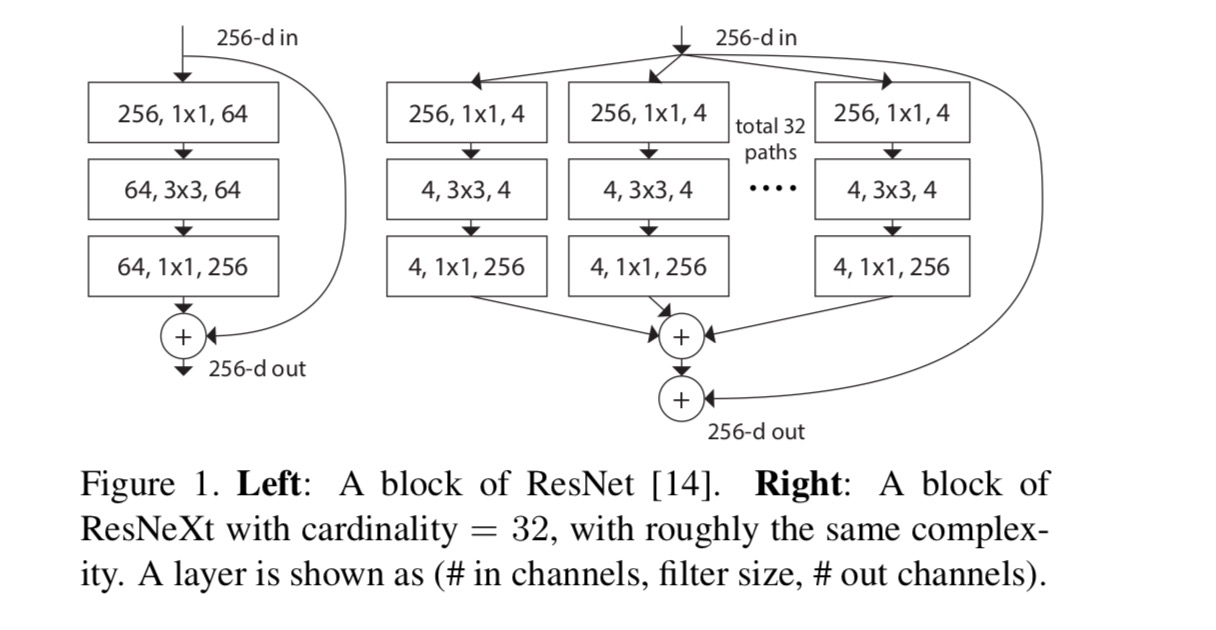
i detta dokument presenterar vi en enkel arkitektur som antar VGG/ResNets strategi att upprepa lager, samtidigt som man utnyttjar split-transform-merge-strategin på ett enkelt, utbyggbart sätt. En modul i vårt nätverk utför en uppsättning transformationer, var och en på en lågdimensionell inbäddning, vars utgångar aggregeras genom summering. Vi strävar efter en enkel realisering av den här tanken — de omvandlingar som ska aggregeras är alla av samma topologi. Denna design gör det möjligt för oss att utvidga till ett stort antal omvandlingar utan specialiserade mönster.

vi visar empiriskt att våra aggregerade transformationer överträffar den ursprungliga ResNet-modulen, även under det begränsade villkoret att upprätthålla beräkningskomplexitet och modellstorlek. Vi betonar att även om det är relativt lätt att öka noggrannheten genom att öka kapaciteten (gå djupare eller bredare), är metoder som ökar noggrannheten samtidigt som (eller minskar) komplexiteten sällsynta i litteraturen.

vår metod indikerar att kardinalitet (storleken på uppsättningen transformationer) är en konkret, mätbar dimension som är av central betydelse, utöver dimensionerna av bredd och djup. Experiment visar att ökande kardinalitet är ett mer effektivt sätt att få noggrannhet än att gå djupare eller bredare, särskilt när djup och bredd börjar ge minskande avkastning för befintliga modeller.

våra neurala nätverk, som heter ResNeXt (föreslår nästa dimension), överträffar ResNet-101/152, ResNet-200, Inception-v3 och Inception-ResNet-v2 på ImageNet-klassificeringsdataset. I synnerhet kan en 101-lagers ResNeXt uppnå bättre noggrannhet än ResNet-200 men har bara 50% komplexitet. Dessutom uppvisar ResNeXt betydligt enklare mönster än alla Inception-modeller.

metod

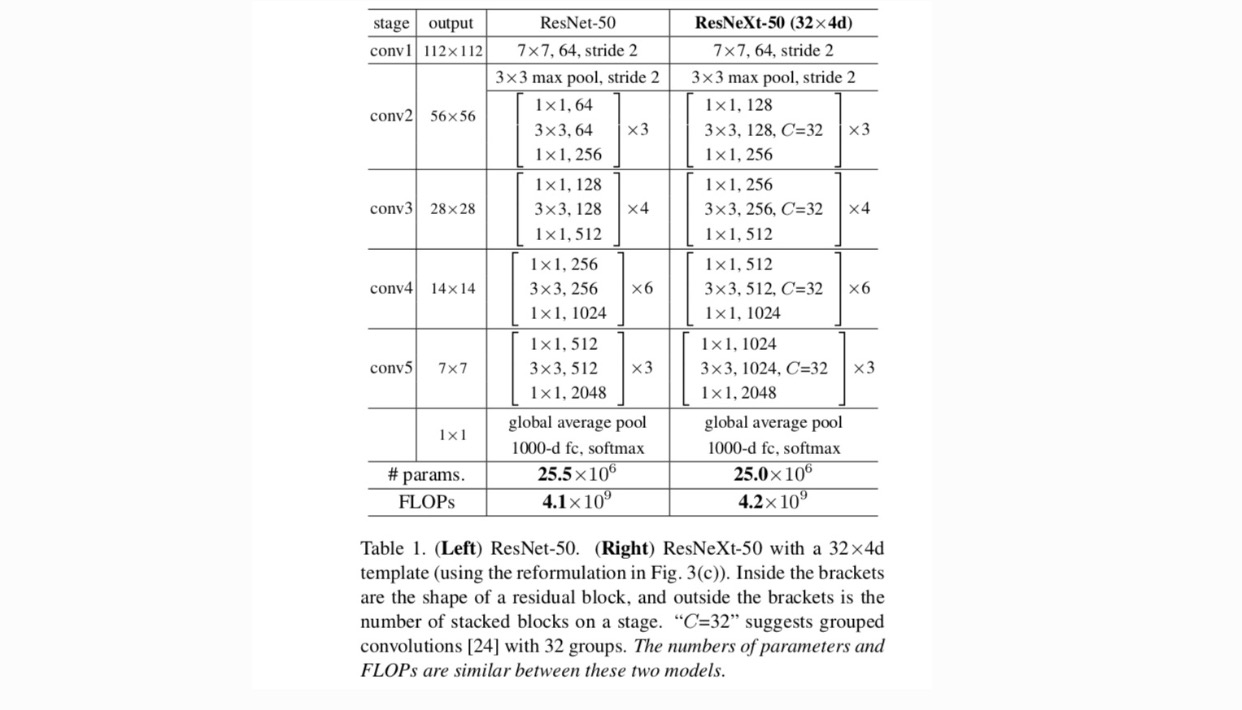
vi antar en mycket modulariserad design efter VGG / ResNets. Vårt nätverk består av en stapel kvarvarande block. Dessa block har samma topologi och är föremål för två enkla regler inspirerade av VGG/ResNets: (1) om de producerar rumsliga kartor av samma storlek delar blocken samma hyperparametrar (bredd och filterstorlekar) och (2) varje gång den rumsliga kartan nedsamplas med en faktor 2 multipliceras blockens bredd med en faktor 2. Den andra regeln säkerställer att beräkningskomplexiteten, när det gäller FLOPs (flytpunktsoperationer, i #av multiply-adds), är ungefär densamma för alla block.

med dessa två regler behöver vi bara designa en mallmodul, och alla moduler i ett nätverk kan bestämmas i enlighet därmed. Så dessa två regler begränsar kraftigt designutrymmet och tillåter oss att fokusera på några viktiga faktorer. De nätverk som konstrueras av dessa regler finns i Tabell 1.

de enklaste neuronerna i artificiella neurala nätverk utför inre produkt (viktad summa), vilket är den elementära omvandlingen som görs av helt anslutna och konvolutionella lager.

ovanstående operation kan omarbetas som en kombination av delning, transformering och aggregering. (1): delning: vektorn skivas som en lågdimensionell inbäddning, och i ovanstående är det en endimensionell delrum (2) transformering: den lågdimensionella representationen transformeras, och i ovanstående är den helt enkelt skalad: (3) aggregering: transformationerna i alla inbäddningar aggregeras av .

Med tanke på ovanstående analys av en enkel neuron överväger vi att ersätta den elementära transformationen (w_i, x_i) med en mer generisk funktion, som i sig också kan vara ett nätverk. Formellt presenterar vi aggregerade transformationer som:

där kan vara en godtycklig funktion. Analogt med en enkel neuron, bör projicera till en (eventuellt lågdimensionell) inbäddning och sedan omvandla den.

vi kallar kardinalitet. är i en position som liknar i, men behöver inte lika och kan vara ett godtyckligt tal. Vi visar genom experiment att kardinalitet är en väsentlig dimension och kan vara effektivare än dimensionerna av bredd och djup.

i denna uppsats anser vi ett enkelt sätt att utforma transformationsfunktionerna: alla har samma topologi. Detta utökar vgg-stilstrategin för att upprepa lager av samma form. Vi ställer in den individuella omvandlingen till den flaskhalsformade arkitekturen som illustreras i Fig. 1 (höger). I det här fallet producerar det första 1-skiktet 1-skiktet i varje lågdimensionell inbäddning.

den aggregerade transformationen i sista ekvationen fungerar som restfunktion:

Var är utgången.

relationerna mellan ResNeXt och Inception-ResNet / Grouped-Convolutions visas i följande figur:

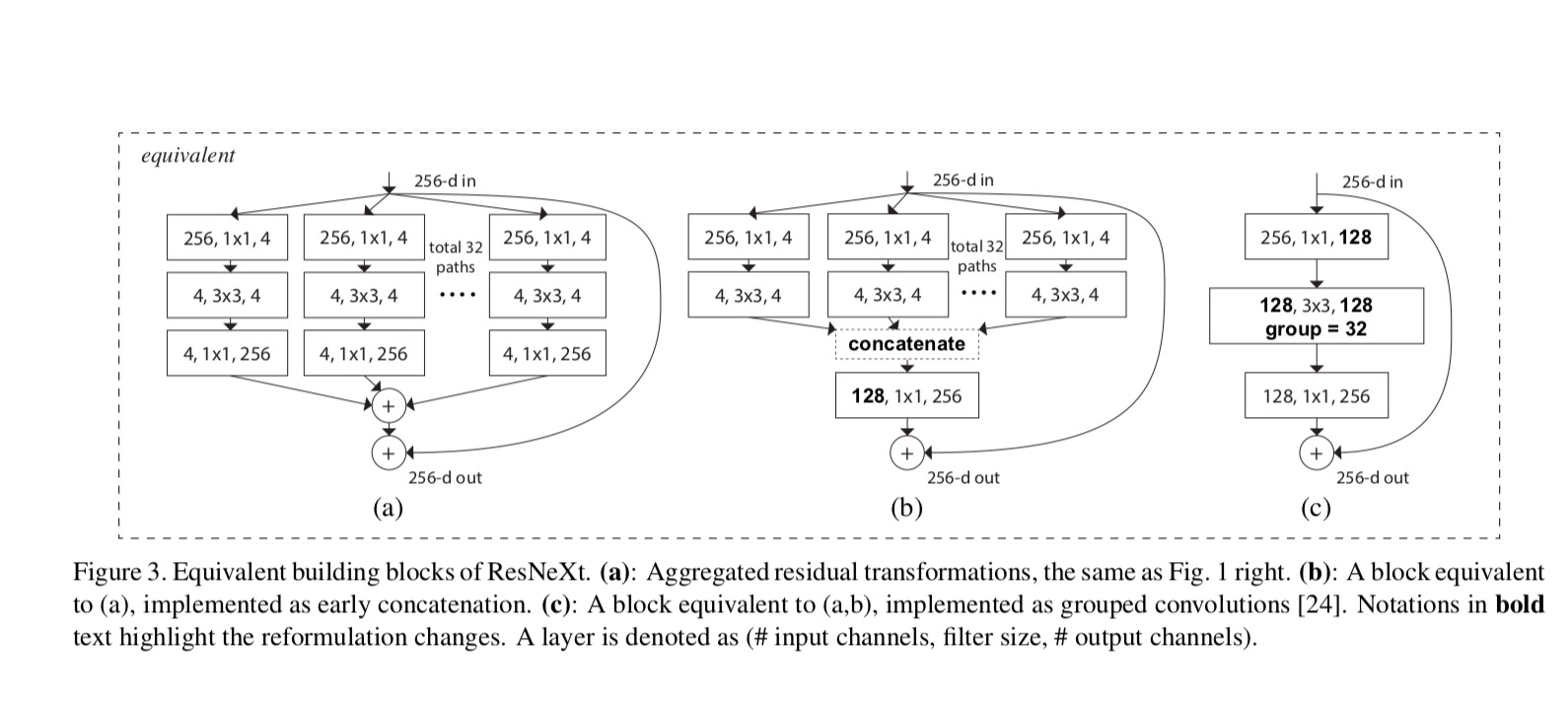
När vi utvärderar olika kardinaliteter samtidigt som vi bevarar komplexiteten vill vi minimera modifieringen av andra hyperparametrar. Vi väljer att justera flaskhalsens bredd(t.ex. 4-d i Fig 1 (höger)), eftersom den kan isoleras från blockets ingång och utgång. Denna strategi introducerar ingen förändring till andra hyper-parametrar (djup eller input/output bredd block), så är till hjälp för oss att fokusera på effekterna av kardinalitet.

i Fig. 1 (Vänster), den ursprungliga ResNet flaskhals blocket har parametrar och proportionella floppar (på samma funktion kartstorlek). Med flaskhalsbredd, vår mall i Fig. 1 (höger) har: parametrar och proportionella floppar. När och, detta nummer . Följande tabell visar förhållandet mellan kardinalitet och flaskhalsbredd .

experiment

kardinalitet vs. bredd. Vi utvärderar först avvägningen mellan kardinalitet och flaskhalsbredd, under bevarad komplexitet enligt Tabell 2. Tabell 3 visar resultaten. Jämfört med ResNet-50 har 32 4D resnext-50 ett valideringsfel på 22,2%, vilket är 1,7% lägre än ResNet-baslinjens 23,9%. Med kardinalitet som ökar från 1 till 32 samtidigt som komplexiteten bibehålls, fortsätter felfrekvensen att minska. Dessutom, 32×4d ResNeXt har också en mycket lägre utbildning fel än ResNet countetpart, vilket tyder på att vinster är inte från legalisering men från och med starkare representation.

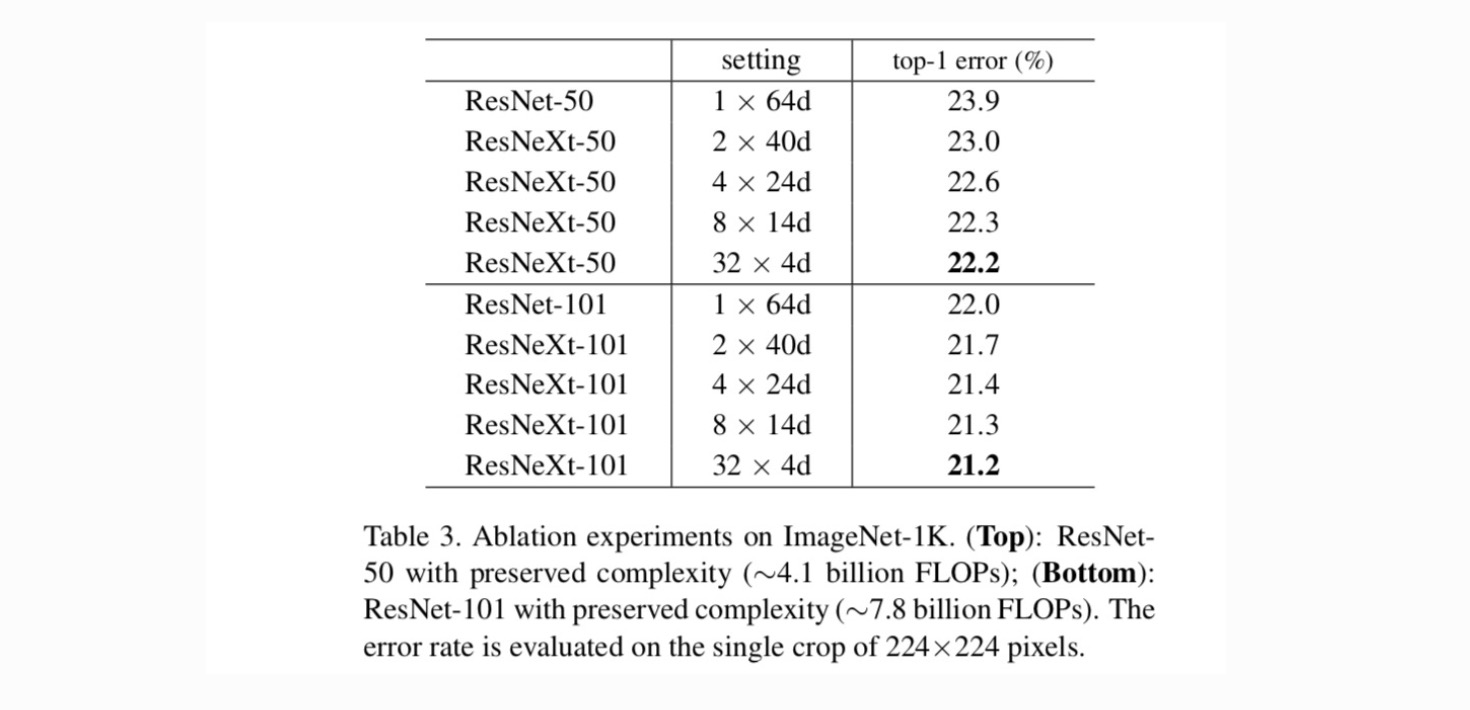
ökande kardinalitet vs. djupare/bredare.

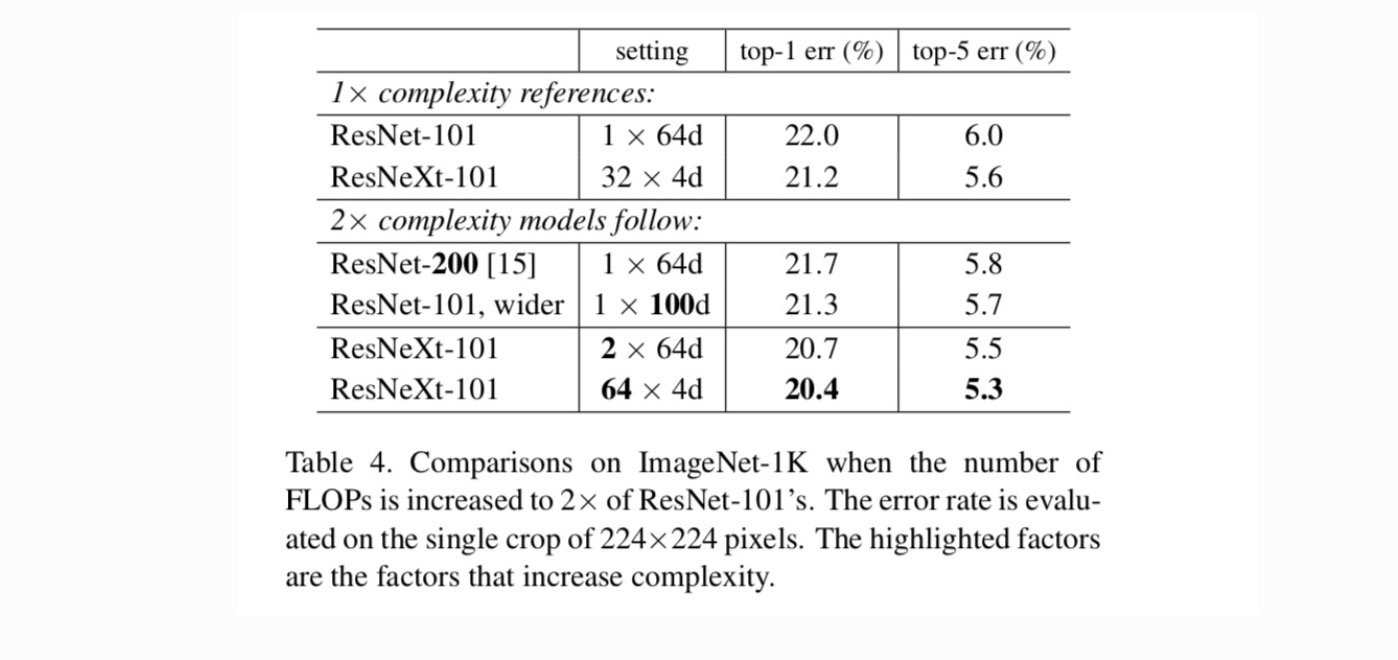
nästa Vi undersöker ökande komplexitet genom att öka kardinalitet C eller öka djup eller bredd. Vi jämför följande varianter (1) som går djupare till 200 lager. Vi antar ResNet-200. (2) gå bredare genom att öka flaskhalsbredden. (3) att öka kardinaliteten genom att fördubbla C.

tabell 4 visar att ökande komplexitet med 2 kcal konsekvent minskar felet jämfört med resnet-101-baslinjen (22,0%). Men förbättringen är liten när man går djupare (ResNet-200, med 0,3%) eller bredare (bredare ResNet-101, med 0,7%). Tvärtom visar ökande kardinalitet C mycket bättre resultat än att gå djupare eller bredare.

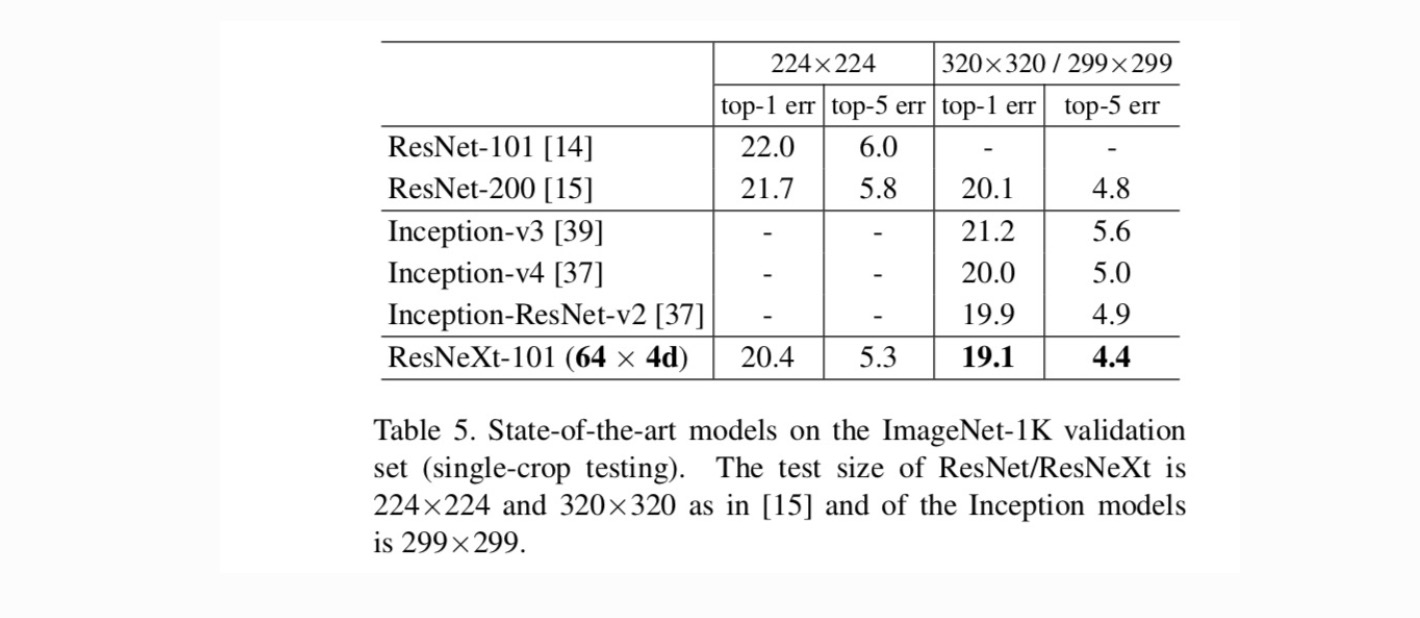
jämförelser med toppmoderna resultat. Tabell 5 visar fler resultat av testning med en gröda på ImageNet-valideringsuppsättningen. Våra resultat jämför sig positivt med ResNet, Inception-v3 / v4 och Inception-ResNet-v2, vilket ger en topp-5-felfrekvens på 4,4%. Dessutom är vår arkitekturdesign mycket enklare än alla Inception-modeller och kräver att betydligt färre hyperparametrar ställs in för hand.