i praktiken av maskin och djupinlärning är modellparametrar egenskaperna hos träningsdata som kommer att lära sig på egen hand under träning av klassificeraren eller annan ML-modell. Till exempel vikter och fördomar, eller delade punkter i beslutsträdet.
Modellhyperparametrar är istället egenskaper som styr hela träningsprocessen. De inkluderar variabler som bestämmer nätverksstrukturen (till exempel antal dolda enheter) och variablerna som bestämmer hur nätverket tränas (till exempel Inlärningsfrekvens). Modell hyperparametrar ställs in före träning (innan du optimerar vikterna och förspänningen).
här är till exempel några inbyggda konfigurationsvariabler för modeller :
- inlärningshastighet
- antal epoker
- dolda lager
- dolda enheter
- Aktiveringsfunktioner
Hyperparametrar är viktiga eftersom de direkt styr beteendet hos träningen algo, vilket har viktig inverkan på prestandan hos modellen under träning.
att välja lämpliga hyperparametrar spelar en nyckelroll i framgången för neurala nätverksarkitekturer, med tanke på påverkan på den lärda modellen. Till exempel, om inlärningshastigheten är för låg, kommer modellen att sakna de viktiga mönstren i data; omvänt, om den är hög kan den ha kollisioner.
att välja bra hyperparametrar ger två huvudfördelar:
- effektiv sökning över utrymmet för möjliga hyperparametrar; och
- enklare hantering av en stor uppsättning experiment för hyperparameterinställning.
Hyperparametrar kan grovt delas in i 2 kategorier:
1. Optimizer hyperparametrar,
2. Modellspecifika hyperparametrar
de är mer relaterade till optimerings-och träningsprocessen.
1.1. Inlärningsfrekvens:
om modellinlärningsgraden är alldeles för mindre än optimala värden, tar det mycket längre tid (hundratals eller tusentals) epoker för att nå ett idealiskt tillstånd. Å andra sidan, om inlärningshastigheten är mycket större än optimalt värde, skulle det överskrida det ideala tillståndet och algoritmen kanske inte konvergerar. En rimlig startinlärningsgrad = 0,001.
viktigt att tänka på att:
a) modellen kommer att ha hundratusentals parametrar var och en med sin egen felkurva. B) felkurvor är inte rena u-former; istället tenderar de att ha mer komplexa former med lokala minima.
1.2. Mini-Batch Storlek:
batchstorlek påverkar resurskraven för träningsprocessen, hastigheten och antalet iterationer på ett icke-trivialt sätt.
historiskt har det varit en debatt att göra stokastisk träning där du passar ett enda exempel på datasetet till modellen och, med bara ett exempel, utför ett framåtpass, beräkna felet / backpropagate & Ställ in justerade värden för alla hyperparametrar. Och gör sedan detta igen för varje exempel i datasetet.
eller, kanske bättre att mata hela data till träningssteget och beräkna lutningen med hjälp av felet som genereras genom att titta på alla exempel i datasetet. Detta kallas batchträning.
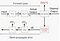
vanlig teknik idag är att ställa in en mini-batchstorlek. Stokastisk träning är när minibatch size =1, och Batch Training är när mini-batch size = antal exempel i träningsuppsättningen. Rekommenderade startvärden för experiment: 1, 2, 4, 8, 16, 32, 64, 128, 256.
en större mini-batchstorlek möjliggör beräkningsförstärkningar som använder matrismultiplikation i träningsberäkningarna . Det kommer dock på bekostnad av att behöva mer minne för träningsprocessen. En mindre mini-batchstorlek inducerar mer brus i felberäkningar, ofta mer användbart för att förhindra att träningsprocessen stannar vid lokala minima. Ett verkligt värde för mini-batch storlek= 32.
Så, medan beräkningsförstärkningen driver oss för att öka mini-batchstorleken, stimulerar denna praktiska algoritmiska fördel att faktiskt göra den mindre.
1.3. Antal epoker:
för att välja rätt antal epoker för träningssteget är det metriska vi bör uppmärksamma valideringsfelet.
det intuitiva manuella sättet är att ha modelltåget för så många antal iterationer så länge valideringsfelet fortsätter att minska.
det finns en teknik som kan användas med namnet Early Stop för att bestämma när man ska sluta träna modellen; det handlar om att stoppa träningsprocessen om valideringsfelet inte har förbättrats under de senaste 10 eller 20 epokerna.
2. Modell Hyperparametrar
de är mer involverade i modellens struktur:
2.1. Antal dolda enheter:
antal dolda enheter är en av de mer mystiska hyperparametrarna. Låt oss komma ihåg att neurala nätverk är universella funktionsproximatorer, och för att de ska lära sig att approximera en funktion (eller en förutsägelsesuppgift) måste de ha tillräckligt med kapacitet för att lära sig funktionen. Antalet dolda enheter är det viktigaste måttet på modellens inlärningskapacitet.
för en enkel funktion kan det behöva färre antal dolda enheter. Ju mer komplex funktionen är, desto mer inlärningskapacitet behöver modellen.
något mer antal enheter då optimalt antal är inte ett problem, men ett mycket större antal kommer att leda till överfitting (dvs. om du ger en modell med för mycket kapacitet, kan det tendera att overfit, försöker ”memorera” dataset, vilket påverkar kapaciteten att generalisera)
2.2. Första dolda lagret:
en annan heuristik som involverar det första dolda lagret är att inställningen av antalet dolda enheter som är större än antalet ingångar tenderar att möjliggöra bättre resultat i antal uppgifter, enligt empirisk observation.
2.3. Antal lager:
det är ofta så att 3-lagers neurala nät kommer att överträffa ett 2-lager. Men att gå ännu djupare hjälper sällan mycket mer. (undantag är Konvolutionella neurala nätverk, där ju djupare de är desto bättre presterar de).
optimeringstekniker för Hyperparametrar
processen att hitta de mest optimala hyperparametrarna i maskininlärning kallas hyperparameteroptimering.
vanliga algoritmer inkluderar:
- Grid Search
- slumpmässig sökning
- Bayesian optimering
Grid Search
Grid search är en traditionell teknik för att implementera hyperparametrar. Det handlar något om brute force alla kombinationer. Gridsökning kräver att skapatvå uppsättningar hyperparametrar:
- Inlärningsfrekvens
- antal lager
Grid search tränar algoritmen för alla kombinationer med hjälp av två uppsättningar hyperparametrar (inlärningsfrekvens och antal lager) och mäter prestanda med korsvalideringsteknik. Denna valideringsteknik säkerställer att den utbildade modellen får de flesta mönstren från datasetet (en av de bästa metoderna för att utföra validering genom att använda ”K-Fold Cross Validation” som hjälper till att ge gott om data för träning av modellen och gott om data för valideringar).
Rutnätsökningsmetoden är en enklare algoritm att använda men den lider om data har högt dimensionellt utrymme som kallas dimensionalitetens förbannelse.
slumpmässig sökning
slumpmässigt samplar sökutrymmet och utvärderar uppsättningar från en angiven sannolikhetsfördelning. Istället för att försöka kontrollera alla 100 000 prover kan vi till exempel kontrollera 1 000 slumpmässiga parametrar.
nackdelen med att använda den slumpmässiga sökalgoritmen är dock att den inte använder information från tidigare experiment för att välja nästa uppsättning. Dessutom är det svårt att förutsäga nästa experiment.

Bayesian optimering
hyperparameterinställning maximerar modellens prestanda på en valideringsuppsättning. ML algos kräver ofta finjustering av modellhyperparametrar. Tyvärr kallas den inställningen ofta ’svart funktion’ eftersom den inte kan skrivas in i en formel (derivat av funktionen är okända).
ett mer tilltalande sätt att optimera & finjustera hyperparametrar innebär att möjliggöra automatiserad modellinställning-till exempel genom att använda Bayesian optimering. Modellen som används för att approximera objektivfunktionen kallas surrogatmodell. En populär surrogatmodell för Bayesian optimering är Gaussian process (GP). Bayesian optimering fungerar vanligtvis genom att anta att den okända funktionen samplades från en Gaussisk Process (GP) och upprätthåller en bakre fördelning för denna funktion när observationer görs.
det finns två viktiga val att göra när man utför Bayesian optimering:
- Välj prior over-funktioner som kommer att uttrycka antaganden om funktionen som optimeras. För detta väljer vi Gaussisk Process före;
- Därefter måste vi välja en förvärvsfunktion som används för att konstruera en verktygsfunktion från modellen posterior, så att vi kan bestämma nästa punkt att utvärdera.
Gaussisk Process
en Gaussisk process definierar den tidigare fördelningen över funktioner som kan omvandlas till en bakre över funktioner när vi har sett vissa data. Den gaussiska processen använder Kovariansmatris för att säkerställa att värden som är nära varandra. Kovariansmatrisen tillsammans med en genomsnittlig funktion för att mata ut det förväntade värdet(x) definierar en Gaussisk process.
1. Gaussisk process kommer att användas som en prior för Bayesian inferens;
2. Beräkning av den bakre gör att den kan användas för att göra förutsägelser för osynliga testfall.

Acquisition Function
Introducing sampling data into the search space is done by acquisition functions. It helps to maximize the acquisition function to determine the next sampling point. Populära förvärvsfunktioner är
- maximal sannolikhet för förbättring (MPI)
- förväntad förbättring (EI)
- övre Konfidensbunden (UCB)
den förväntade förbättringen (EI) är en populär och definieras som:
EI(x)=https: / / p>
där Bisexuell(x) är den nuvarande optimala uppsättningen hyperparametrar. Maximering av hyperparametrarna kommer att förbättras på Aug.
