Introduktion till Rörelseuppskattning med optiskt flöde

I denna handledning dyker vi in i grunden för optiskt flöde, tittar på några av dess applikationer och implementerar dess två huvudvarianter (glesa och täta). Vi diskuterar också kortfattat nyare tillvägagångssätt med djupt lärande och lovande framtida riktningar.

nya genombrott i datorvisionsforskning har gjort det möjligt för maskiner att uppfatta sin omvärld genom tekniker som objektdetektering för att upptäcka instanser av objekt som tillhör en viss klass och semantisk segmentering för pixelvis klassificering.

för bearbetning av videoingång i realtid adresserar de flesta implementeringar av dessa tekniker emellertid endast relationer mellan objekt inom samma ram \((x, y)\) utan hänsyn till tidsinformation \((t)\). Med andra ord utvärderar de varje ram oberoende, som om de är helt orelaterade bilder, för varje körning. Men vad händer om vi behöver relationerna mellan på varandra följande ramar, till exempel vill vi spåra fordonets rörelse över ramar för att uppskatta dess nuvarande hastighet och förutsäga dess position i nästa ram?

eller, alternativt, vad händer om vi behöver information om mänskliga ställningsförhållanden mellan på varandra följande ramar för att känna igen mänskliga handlingar som Bågskytte, Baseboll och basket?

i denna handledning kommer vi att lära oss vad optiskt flöde är, hur man implementerar sina två huvudvarianter (glesa och täta) och får också en stor bild av nyare tillvägagångssätt som involverar djupt lärande och lovande framtida riktningar.

vad är optiskt flöde?
implementera gles optiskt flöde
implementera tätt optiskt flöde
djupt lärande och bortom

Vad är optiskt flöde?

Låt oss börja med en hög nivå förståelse för optiskt flöde. Optiskt flöde är rörelsen av objekt mellan på varandra följande sekvensramar, orsakad av den relativa rörelsen mellan objektet och kameran. Problemet med optiskt flöde kan uttryckas som:

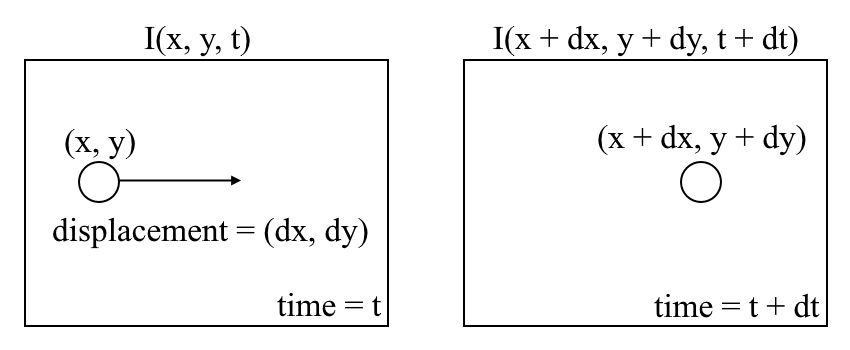
där mellan på varandra följande ramar kan vi uttrycka bildintensiteten \((i)\) som en funktion av rymden \((x, y)\) och tid \((t)\). Med andra ord, om vi tar den första bilden \(i(x, y, t)\) och flyttar dess pixlar med \((dx, dy)\) över \(t\) tid, får vi den nya bilden \(i(x + dx, y + dy, t + dt)\).

först antar vi att pixelintensiteter för ett objekt är konstanta mellan på varandra följande ramar.

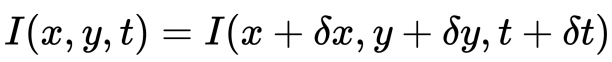
För det andra tar vi Taylor-serien Approximation av RHS och tar bort vanliga termer.

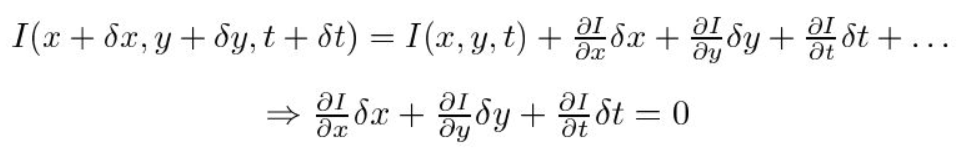
För det tredje delar vi med \(dt\) för att härleda den optiska flödesekvationen:

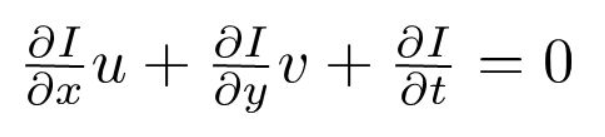
där \(u = dx/dt\) och \(v = dy/dt\).

\(dI/dx, dI/dy\) och \(dI / dt\) är bildgradienterna längs den horisontella axeln, den vertikala axeln och tiden. Därför avslutar vi med problemet med optiskt flöde, det vill säga att lösa \(u (dx/dt)\) och \(v (dy/dt)\) för att bestämma rörelse över tiden. Du kanske märker att vi inte direkt kan lösa den optiska flödesekvationen för \(u\) och \(v\) eftersom det bara finns en ekvation för två okända variabler. Vi kommer att implementera några metoder som Lucas-Kanade-metoden för att lösa problemet.

gles vs tät optiskt flöde

gles optiskt flöde ger flödesvektorerna för några ”intressanta funktioner” (säg några pixlar som visar kanterna eller hörnen på ett objekt) inom ramen medan tätt optiskt flöde, vilket ger flödesvektorerna för hela ramen (alla pixlar) – upp till en flödesvektor per pixel. Som du skulle ha gissat har tätt optiskt flöde högre noggrannhet till kostnaden för att vara långsam/beräkningsmässigt dyr.

implementera gles optiskt flöde

gles optiskt flöde väljer en gles funktionsuppsättning pixlar (t.ex. intressanta funktioner som kanter och hörn) för att spåra dess hastighetsvektorer (rörelse). De extraherade funktionerna passeras i den optiska flödesfunktionen från RAM till ram för att säkerställa att samma punkter spåras. Det finns olika implementeringar av gles optiskt flöde, inklusive Lucas–Kanade–metoden, Horn–Schunck-metoden, Buxton-Buxton-metoden och mer. Vi kommer att använda Lucas-Kanade-metoden med OpenCV, ett open source-bibliotek med datorsynalgoritmer, för implementering.

ställa in din miljö

om du inte redan har OpenCV installerat, öppna Terminal och kör:

pip install opencv-python

klona nu handledningsförvaret genom att köra:

git clone https://github.com/chuanenlin/optical-flow.git

nästa, öppna sparse-starter.py med din textredigerare. Vi kommer att skriva all kod i denna Python-fil.

konfigurera OpenCV för att läsa en video och ställa in parametrar

Shi-Tomasi Corner Detector – välja pixlar för att spåra

för implementering av gles optiskt flöde spårar vi bara rörelsen för en funktionsuppsättning pixlar. Funktioner i bilder är intressanta platser som presenterar rik bildinnehållsinformation. Sådana funktioner kan till exempel vara punkter i bilden som är oföränderliga för översättning, skala, rotation och intensitetsförändringar som hörn.shi-Tomasi Corner Detector är mycket lik den populära Harris Corner Detector som kan implementeras med följande tre procedurer:

1. Bestäm fönster (små bildpatchar) med stora gradienter (variationer i bildintensitet) när de översätts i både \(x\) och \(y\) riktningar.
2. för varje fönster, beräkna en poäng \(R\).
3. beroende på värdet på \(R\) klassificeras varje fönster som en platt, kant eller hörn.

Om du vill veta mer om en steg-för-steg matematisk förklaring av Harris Corner Detector, Känn dig fri att gå igenom dessa bilder.Shi och Tomasi gjorde senare en liten men effektiv modifiering av Harris Corner Detector i sina papper bra funktioner att spåra.

modifieringen är till ekvationen där score \(R\) beräknas. I Harris Corner Detector ges poängfunktionen av:

$$
\begin{array}{c}{R=\operatorname{det} M-k(\operatorname{trace} M)^{2}}\newline \
{\operatorname{det} M=\lambda_{1} \lambda_{2}}\newline \
{\operatorname{trace} M=\lambda_{1}+\lambda_{2}}\end{array}
$$

istället föreslog shi-Tomasi poängfunktionen som:

$$
r=\min \vänster(\lambda_{1}, \lambda_{2}\höger)
$$

vilket i princip betyder att om \(R\) är större än ett tröskelvärde klassificeras det som ett hörn. Följande jämför scoringfunktionerna för Harris (vänster) och Shi-Tomasi(höger) i \(8-2\) Utrymme.

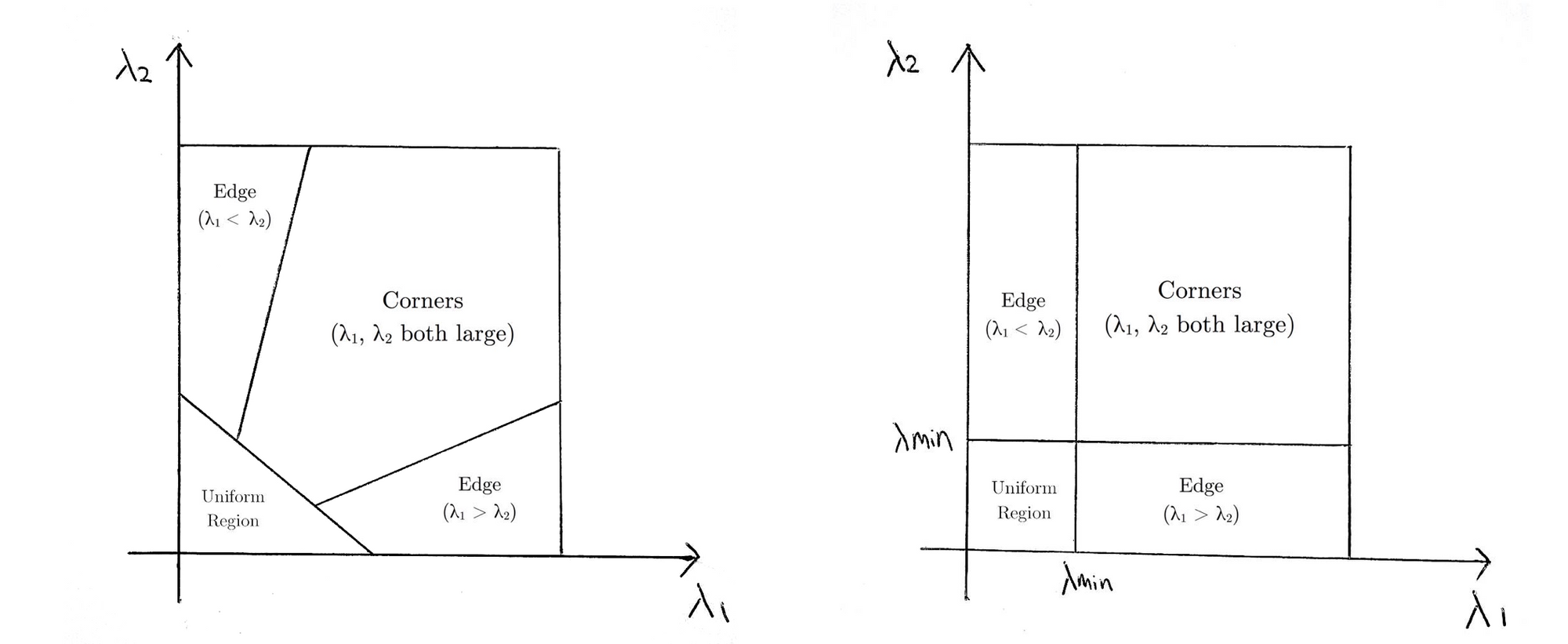
För Shi-Tomasi är fönstret endast klassificerat som ett hörn när \(1\) och \(2\) ligger över en minimitröskel \(2\).

dokumentationen av Opencvs implementering av Shi-Tomasi via goodFeaturesToTrack() kan hittas här.

spåra specifika objekt

det kan finnas scenarier där du bara vill spåra ett specifikt objekt av intresse (säg att spåra en viss person) eller en kategori av objekt (som alla 2 wheeler-fordon i trafik). Du kan enkelt ändra koden för att spåra pixlarna för objektet/objekten du vill ha genom att ändra variabeln prev.

Du kan också kombinera objektdetektering med den här metoden för att bara uppskatta flödet av pixlar i de upptäckta avgränsningsrutorna. På så sätt kan du spåra alla objekt av en viss typ/kategori i videon.

Lucas-Kanade: gles optiskt flöde

Lucas och Kanade föreslog en effektiv teknik för att uppskatta rörelsen av intressanta funktioner genom att jämföra två på varandra följande ramar i deras papper en iterativ Bildregistreringsteknik med en applikation för Stereosyn. Lucas – Kanade-metoden fungerar under följande antaganden:

1. två på varandra följande ramar separeras med en liten tidsökning (\(dt\)) så att objekt inte förskjuts avsevärt (med andra ord fungerar metoden bäst med långsamma objekt).
2. en ram skildrar en” naturlig ” scen med texturerade föremål som uppvisar gråtoner som förändras smidigt.

först, under dessa antaganden, kan vi ta ett litet 3×3-fönster (grannskap) runt de funktioner som upptäckts av Shi-Tomasi och antar att alla nio punkter har samma rörelse.

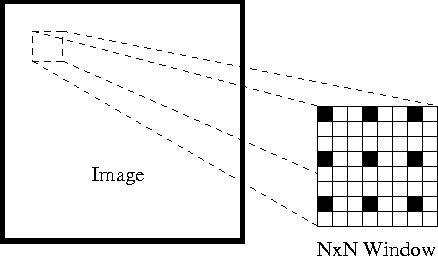
detta kan representeras som

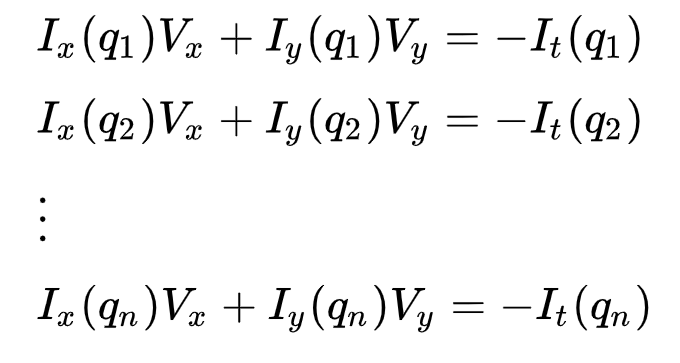
där \(q_1, q_2, …, q_n\) betecknar pixlarna inuti fönstret (t.ex. \(n\) = 9 för ett 3×3-fönster) och \(i_x(q_i)\), \(i_y(q_i)\) och \(i_t(q_i)\) betecknar de partiella derivaten av bilden \(i\) med avseende på Position \((X, Y)\) och tid \(T\), för pixel \(q_i\) vid den aktuella tiden.

detta är bara den optiska Flödesekvationen (som vi beskrev tidigare) för var och en av n-pixlarna.

uppsättningen ekvationer kan representeras i följande matrisform där \(av = b\):

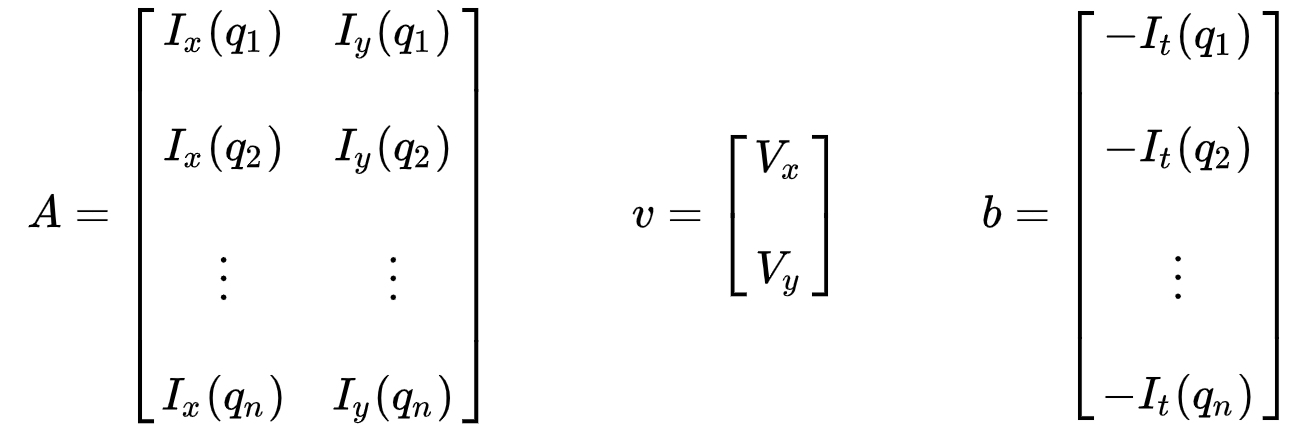
notera att tidigare (se ”vad är optiskt flöde?”avsnitt) stod vi inför frågan om att behöva lösa för två okända variabler med en ekvation. Vi måste nu lösa två okända (\(V_x\) och \(V_y\)) med nio ekvationer, som är överbestämda.

För det andra, för att ta itu med det överbestämda problemet, tillämpar vi minsta kvadrater som passar för att erhålla följande två-ekvation-två-okänt problem:

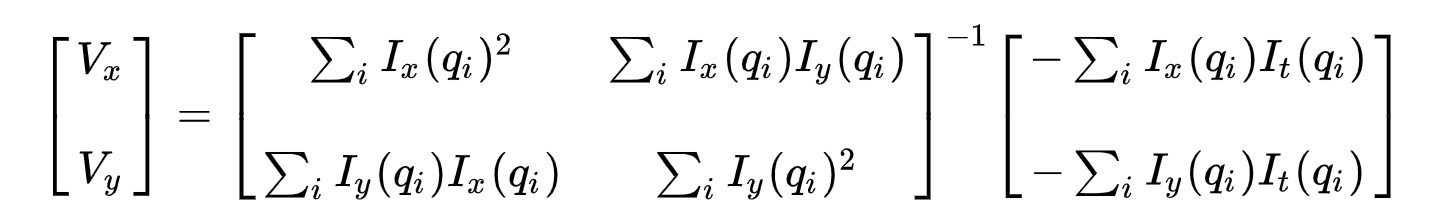
där \(VX = u = DX/dt\) betecknar rörelsen av \(X\) över tiden och \(vy = v = dy/dt\) betecknar rörelsen av Y över tiden. Att lösa för de två variablerna fullbordar det optiska flödesproblemet.

i ett nötskal identifierar vi några intressanta funktioner för att spåra och iterativt beräkna de optiska flödesvektorerna för dessa punkter. Att anta Lucas-Kanade-metoden fungerar dock bara för små rörelser (från vårt ursprungliga antagande) och misslyckas när det finns stor rörelse. Därför antar OpenCV-implementeringen av Lucas-Kanade-metoden pyramider.

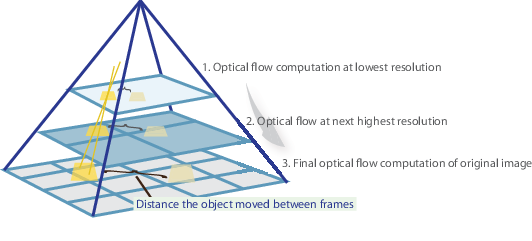
i en vy på hög nivå försummas små rörelser när vi går upp i pyramiden och stora rörelser reduceras till små rörelser-vi beräknar optiskt flöde tillsammans med skalan. En omfattande matematisk förklaring av Opencvs implementering finns i Bouguets anteckningar och dokumentationen av Opencvs implementering av Lucas-Kanade-metoden via calcOpticalFlowPyrLK() finns här.

visualisera

och det är det! Öppna Terminal och kör

python sparse-starter.py

för att testa din glesa optiska flödesimplementering.

om du har missat någon kod kan den fullständiga koden hittas i sparse-solution.py.

implementera tätt optiskt flöde

Vi har tidigare beräknat det optiska flödet för en gles funktionsuppsättning pixlar. Tätt optiskt flöde försöker beräkna den optiska flödesvektorn för varje pixel i varje ram. Medan en sådan beräkning kan vara långsammare, ger det ett mer exakt resultat och ett tätare resultat som är lämpligt för applikationer som inlärningsstruktur från rörelse och videosegmentering. Det finns olika implementeringar av tätt optiskt flöde. Vi kommer att använda Farneback-metoden, en av de mest populära implementeringarna, med att använda OpenCV, ett open source-bibliotek med datorvisionsalgoritmer, för implementering.

ställa in din miljö

om du inte redan har gjort det, Följ steg 1 för att implementera gles optical flow för att ställa in din miljö.

nästa, öppna dense-starter.py med din textredigerare. Vi kommer att skriva all kod i denna Python-fil.

konfigurera OpenCV för att läsa en video

Farneback Optical Flow

Gunnar Farneback föreslog en effektiv teknik för att uppskatta rörelsen av intressanta funktioner genom att jämföra två på varandra följande ramar i hans papper två-Frame Motion Estimation baserat på polynom Expansion.

För det första approximerar metoden windows (se Lucas Kanade-avsnittet för gles optisk flödesimplementering för mer information) av bildramar av kvadratiska polynom genom polynomexpansionstransformering. För det andra, genom att observera hur polynomet transformeras under översättning (rörelse), definieras en metod för att uppskatta förskjutningsfält från polynomutvidgningskoefficienter. Efter en serie förfiningar beräknas tätt optiskt flöde. Farnebacks papper är ganska kortfattat och enkelt att följa så jag rekommenderar starkt att gå igenom papperet om du vill ha en större förståelse för dess matematiska härledning.

För Opencvs implementering beräknar den storleken och riktningen för optiskt flöde från en 2-kanals uppsättning flödesvektorer \((dx/dt, dy/dt)\), det optiska flödesproblemet. Det visualiserar sedan vinkeln (riktning) av flödet med nyans och avståndet (magnitud) av flödet med värdet av HSV-färgrepresentation. Styrkan hos HSV är alltid inställd på maximalt 255 för optimal synlighet. Dokumentationen av Opencvs implementering av Farneback-metoden via calcOpticalFlowFarneback() kan hittas här.

visualisera

och det är det! Öppna Terminal och kör

python dense-starter.py

för att testa din täta optiska flödesimplementering.

om du har missat någon kod kan den fullständiga koden hittas i dense-solution.py.

optiskt flöde med Deep Learning

medan problemet med optiskt flöde historiskt har varit ett optimeringsproblem, har de senaste metoderna genom att tillämpa deep learning visat imponerande resultat. I allmänhet tar sådana tillvägagångssätt två videoramar som ingång för att mata ut det optiska flödet( färgkodad bild), vilket kan uttryckas som:

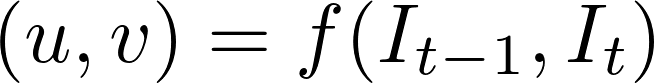
där \(u\) är rörelsen i \(x\) riktningen, \(v\) är rörelsen i \(y\) riktningen och \(f\) är ett neuralt nätverk som tar in två på varandra följande ramar \(i_{t-1}\) (ram vid tiden = \(t-1)\) och \(I_t\) (RAM vid tiden = \(t)\) som input.

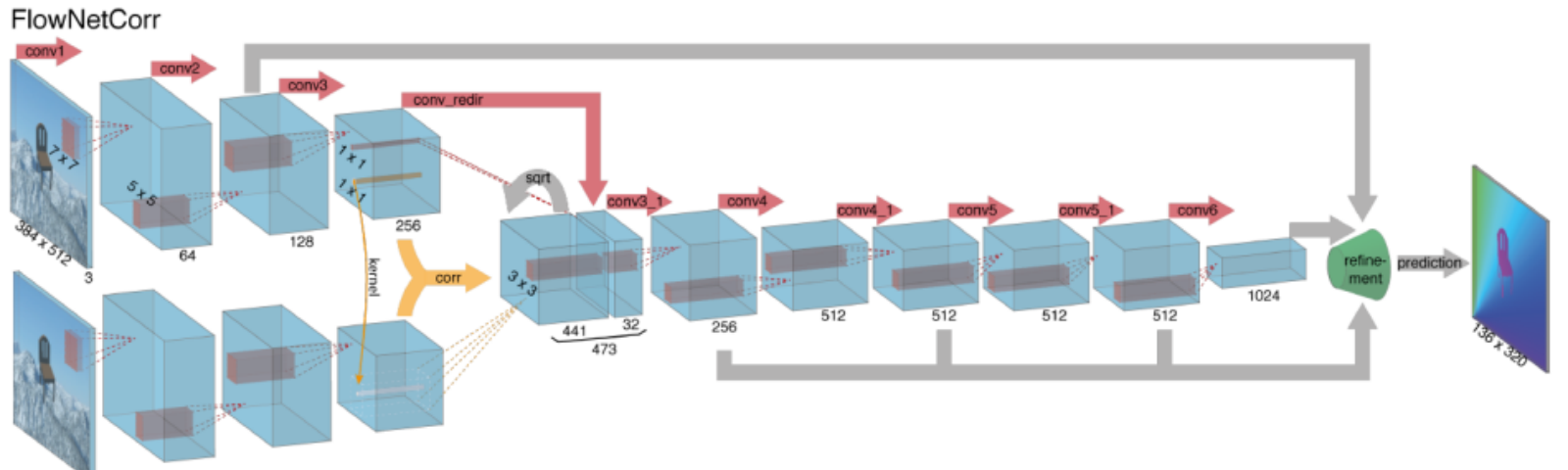
beräkning av optiskt flöde med djupa neurala nätverk kräver stora mängder träningsdata vilket är särskilt svårt att erhålla. Detta beror på att märkning av videofilmer för optiskt flöde kräver exakt att man bestämmer den exakta rörelsen för varje punkt i en bild till subpixelnoggrannhet. För att ta itu med frågan om märkning av träningsdata använde forskare datorgrafik för att simulera massiva realistiska världar. Eftersom världarna genereras genom instruktion är rörelsen för varje punkt i en bild i en videosekvens känd. Några exempel på sådana inkluderar MPI-Sintel, en CGI-film med öppen källkod med optisk flödesmärkning gjord för olika sekvenser och flygande stolar, en dataset av många stolar som flyger över slumpmässiga bakgrunder också med optisk flödesmärkning.

att lösa optiska flödesproblem med djupt lärande är ett extremt hett ämne just nu, med varianter av FlowNet, SPyNet, PWC-Net och mer som överträffar varandra på olika riktmärken.

optiskt flöde ansökan: semantisk segmentering

det optiska flödesfältet är en stor gruva av information för den observerade scenen. Eftersom teknikerna för exakt bestämning av optiskt flöde förbättras är det intressant att se tillämpningar av optiskt flöde i korsning med flera andra grundläggande datorvisionsuppgifter. Till exempel är uppgiften för semantisk segmentering att dela upp en bild i serier av regioner som motsvarar unika objektklasser, men nära placerade objekt med identiska texturer är ofta svåra för segmenteringstekniker med en ram. Om objekten placeras separat kan emellertid objektens distinkta rörelser vara till stor hjälp där diskontinuitet i det täta optiska flödesfältet motsvarar gränserna mellan objekt.

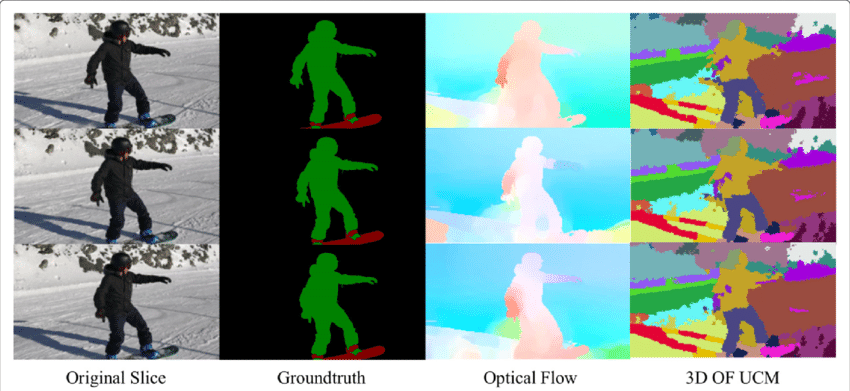
optisk Flödesapplikation: objektdetektering& spårning

en annan lovande tillämpning av optiskt flöde kan vara med objektdetektering och spårning eller, i en högnivåform, mot att bygga fordonsspårnings-och trafikanalyssystem i realtid. Eftersom sparsamt optiskt flöde använder spårning av intressanta platser kan sådana realtidssystem utföras med funktionsbaserade optiska flödestekniker från antingen från en stationär kamera eller kameror anslutna till fordon.

slutsats

i grund och botten fungerar optiska flödesvektorer som inmatning till en myriad av högre nivåuppgifter som kräver scenförståelse av videosekvenser medan dessa uppgifter ytterligare kan fungera som byggstenar till ännu mer komplexa system som ansiktsuttrycksanalys, autonom fordonsnavigering och mycket mer. Nya applikationer för optiskt flöde som ännu inte upptäckts begränsas endast av dess designers uppfinningsrikedom.

lat för att koda, vill du inte spendera på GPU: er? Gå över till Nanonets och bygg datorvisionsmodeller gratis!