Magic of the Sobel Operator

slutligen, det ögonblick du alla har väntat på, nästa i vår unsupervised Bayesian inference Series: vår (inte så) djupdykning i Sobel-operatören.

en verkligt magisk kantdetekteringsalgoritm, det möjliggör extraktion på låg nivå och dimensioneringsreduktion, vilket väsentligen minskar bruset i bilden. Det har varit särskilt användbart i ansiktsigenkänningsapplikationer.

1968 kärleksbarn av Irwin Sobel och Gary Feldman (Stanford Artificial Intelligence Laboratory), denna algoritm var inspiration för många moderna kantdetekteringstekniker. Genom att sammanfoga två motsatta kärnor eller masker över en given bild (t. ex. se nedan-vänster) (var och en kan upptäcka antingen horisontella eller vertikala kanter), kan vi skapa en mindre bullrig, utjämnad representation (se nedan-höger).

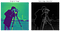
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel värden (vanligtvis luminans) genom att differentiera skillnaden mellan varje pixel (ankarpixeln) och dess omgivande pixlar (i huvudsak approximera derivatet av en bild).

detta resulterar i utjämning av originalbilden och ger en lägre dimension, där geometriska funktioner på låg nivå kan ses tydligare. Dessa utgångar kan sedan användas som ingångar till mer komplexa klassificeringsalgoritmer, eller som exempel som används för oövervakad probabilistisk kluster via Kullback-Leibler divergens (KLD) (som ses i min senaste blogg på LBP).

att generera vår lägre dimensionsutgång kräver att vi tar derivatet av bilden. Först beräknar vi derivatet i både X-och y-riktningarna. Vi skapar två 3×3-kärnor (se matriser), med nollor längs mitten av motsvarande axel, två i mittrutorna vinkelrätt mot den centrala nollan och de i var och en av hörnen. Var och en av icke-nollvärdena bör vara positiva ovanpå/till höger om nollorna (beroende på axel) och negativa på motsvarande sida. Dessa kärnor heter Gx och Gy.

dessa visas i formatet:

dessa kärnor kommer sedan att kretsa över vår bild och placera den centrala pixeln i varje kärna över varje pixel i bilden. Vi använder matrismultiplikation för att beräkna intensitetsvärdet för en ny motsvarande pixel i en utgångsbild för varje kärna. Därför slutar vi med två utgångsbilder (en för varje kartesisk riktning).

målet är att hitta skillnaden / förändringen mellan pixeln i bilden och alla pixlar i gradientmatrisen (kärnan) (Gx och Gy). Mer matematiskt kan detta uttryckas som.

sidoanteckning:

Vi är tekniskt inte convolving något. Även om vi vill hänvisa till ’omvälvningar’ i AI-och maskininlärningscirklar, skulle en omvälvning innebära att man vänder originalbilden. Matematiskt sett, när vi hänvisar till omvälvningar, beräknar vi verkligen korskorrelationen mellan varje 3×3-område i ingången och masken för varje pixel. Utmatningsbilden är den totala kovariansen mellan masken och ingången. Så här upptäcks kanterna.

tillbaka till vår sobel förklaring…

de beräknade värdena för varje matrismultiplikation mellan masken och 3×3-delen av ingången summeras för att producera det slutliga värdet för pixeln i utgångsbilden. Detta genererar en ny bild som innehåller information om förekomsten av vertikala och horisontella kanter som finns i originalbilden. Detta är en geometrisk funktionsrepresentation av originalbilden. Vidare, eftersom denna operatör är garanterad att producera samma utgång varje gång, möjliggör denna teknik stabil kantdetektering för bildsegmenteringsuppgifter.

från dessa utgångar kan vi beräkna både gradientstorleken och gradientriktningen (med hjälp av arctangent-operatören) vid en given pixel (x, y):

från detta kan vi konstatera att de pixlar med stora storheter är mer benägna att vara en kant i bilden,medan riktningen informerar oss om kantorienteringen (även om riktningen inte behövs för att generera vår produktion).

en enkel implementering:

Här är en enkel implementering av sobel-operatören i python (med NumPy) för att ge dig en känsla för processen (för alla er spirande kodare där ute).

denna implementering är en python-variant av Wikipedia pseudokodsexemplet, som syftar till att visa hur du kan implementera denna algoritm, samtidigt som du visar de olika stegen i processen.

varför bryr vi oss?

Även om gradient approximationen som produceras av denna operatör är relativt rå, ger den en extremt beräkningseffektiv metod för beräkning av kanter, hörn och andra geometriska egenskaper hos bilder. I sin tur har det banat väg för ett antal dimensioneringsreducerings-och funktionsextraktionstekniker, till exempel lokala binära mönster (se min andra blogg för mer information om denna teknik).

att förlita sig på uteslutande geometriska funktioner riskerar att förlora viktig information under kodningen av våra data, men avvägningen är det som möjliggör snabb förbehandling av data och i sin tur snabb träning. Därför är denna teknik särskilt användbar i scenarier där textur och geometriska egenskaper kan anses vara mycket viktiga för att definiera ingången. Det är därför ansiktsigenkänning kan slutföras med en relativt hög grad av noggrannhet med hjälp av sobel-operatören. Denna teknik kan dock inte vara det bästa valet om man försöker klassificera eller gruppera ingångar som använder färg som sin huvudsakliga differentierande faktor.

denna metod är fortfarande extremt effektiv för att få en lågdimensionell representation av geometriska egenskaper och en utmärkt utgångspunkt för dimensionalitet och brusreducering, före användning av andra klassificerare eller för användning i Bayesianska inferensmetoder.