postat juni 2008.
den andra av två kolumner på matematiken för mätning (den första är här). …
Bill Casselman
University of British Columbia, Vancouver, Kanada
cass at math.ubc.ca
John Eggers
University of California, San Diego
jaggare vid ucsd.edu
 e-post till en vän e-post till en vän |
 skriv ut den här artikeln skriv ut den här artikeln |
en Planimeter är ett Bordsinstrument för mätning av områden, vanligtvis områden med oregelbundna regioner på en karta eller ett fotografi. De var en gång vanliga, men har nu till stor del ersatts av digitala verktyg.
följande bild ger en uppfattning om installationen. Polarmen roterar fritt runt polen, som är fixerad på bordet. Spårarmen roterar runt pivoten, det är där den ansluter sig till polararmen. Du spårar en kurva medurs med spåraren, och när du gör det rullar mäthjulet längs, och det totala avståndet det rullar ackumuleras på ratten. Stödhjulet hindrar saken från att floppa över. I slutet läser du av ett nummer från ratten, och efter multiplikation med en faktor beroende endast på planimeterns speciella konfiguration får du området inuti kurvan.

nästa figur ger dig en bättre bild av mekanismen.

vi kallar Vagnen montering av hjul, ratt och pivot. I nästa bild får du en bättre titt på den och kan se maskdrivningen som får ratten att rotera när mäthjulet rör sig.

här är diagrammet för den ursprungliga planimetern, från artikeln av Jakob Amsler som introducerade den:
hur kan en så enkel sak mäta områden?
Planimeterns geometri
planimeterns medurs rörelse är riktningen motsatt vad matematiker har bestämt bör vara positiv rotation. I stället för att bryta mot denna konvention kommer vi från och med nu att arbeta med en matematiker planimeter, där du rör dig moturs. Liksom andra matematikers fantasier finns det ingen på planeten!
det finns vissa begränsningar för hur du placerar planimetern med avseende på kurvan du vill spåra. Vagnen kan skjutas längs spårarmen, men i alla fall är längden l på spårarmen mindre än längden r på polarmen. Detta innebär att spåraren aldrig kan komma inom ett avstånd r – l av Polen. Å andra sidan, när den är helt utsträckt, kan spåraren aldrig nå bortom r + l. så kurvan som ska spåras måste ligga inom ringen mellan två cirklar, en med radie r – l, den andra r + l.

faktum är att det i ett ögonblick bör bli klart att armarna aldrig ska förlängas helt, så kurvan som ska spåras måste ligga helt inuti ringen. Dessutom placeras normalt Polen på utsidan av kurvan.

För en given punkt i ringen finns det exakt två möjliga konfigurationer av planimetern som placerar spåraren på den punkten. Att välja en punkt eller det andra betyder att man väljer ett tecken för en kvadratrot. Vi kallar detta att välja en orientering för planimetern. Det är positivt om kvadratroten är positiv. När en orientering har valts kommer den att förbli densamma om inte armen är helt utsträckt. Detta får aldrig hända. Så länge din kurva är helt inom ringen, kommer planimeterns konfigurationer att variera smidigt och unikt med spårarens väg.
nästa sak att göra är att förstå några saker om mäthjulets rörelse. Som följande bild visar, om hjulet färdas i en rak linje ett avstånd C, hjulet roterar genom en vinkel Asia = C / R där R är dess radie.

så det är verkligen sant att hjulets rotation och avståndet som reste av spårarmen har något förhållande till varandra. Men det här förhållandet är lite subtilt. Om armen bara rör sig rakt fram ett avstånd C, området sopas ut kommer att vara lC, men om det skiftar parallellt med sig själv området sopas ut kommer att vara 0. I det första fallet kommer en punkt på hjulets omkrets att flytta avstånd C. I det andra fallet kommer hjulet inte att röra sig alls. Och om armen översätter snett, roterar hjulet ett avstånd som är lika med höjden på parallellogrammet som täcks av armen. I alla fall där armen översätts parallellt med sig själv, kommer området som sveps ut av delen av spårarmen mellan pivoten och spåraren att vara lika med lC, där C är avståndet mätt genom hjulets rotation. Detta är det grundläggande faktum som relaterar armens rörelse till mäthjulets rörelse.

sättet att uttrycka detta exakt är att oavsett hur armen rör sig, är avståndet som mäts av hjulet vägen integral

där exporten är den väg som reste av den punkt på armen där mäthjulet är fäst, n är enhetsvektorn vinkelrätt mot mäthjulet arm när som helst, och T är enhetsvektorn som pekar i färdriktningen (så att till exempel om armen rör sig parallellt med sig är punktprodukten av n och T 0).
Guldin ’ s Theorem
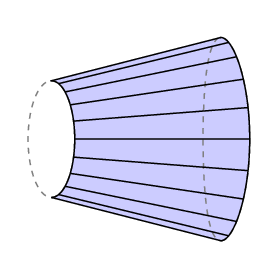
nästa ska vi försöka göra planimeterns beteende intuitivt klart, men först ska vi titta på en speciell typ av planimeter, och i detta fall bevisa ett mer allmänt resultat. Antag att vi tar en enda fritt rörlig arm med Längd l och fäster ett mäthjul med radie R mitt i centrum.

sedan flyttar vi armen runt på planet. Om mäthjulet roterar genom en total vinkel på radianer i enlighet med den hastighet som armen rör sig runt, är avståndet som en punkt på omkretsen rör sig C = i enlighet med den.
Guldins Sats. I denna situation är det totala området som sveps ut av armen produkten lC.
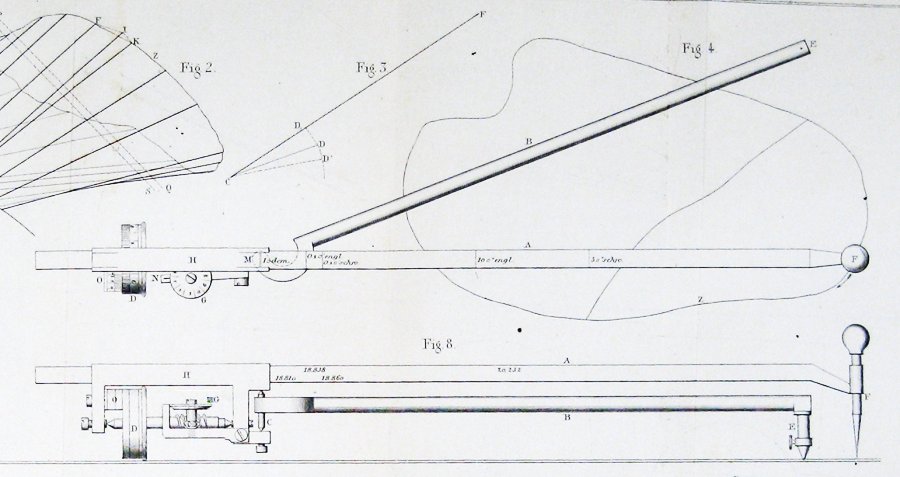
område här tolkas med ett tecken. Om armen bara roterar runt sitt centrum, går den ena halvan av armen framåt och den andra bakåt, och de två avbryter.
Vi har redan sett att Guldins påstående är giltigt i det fall armen bara översätter. Naturligtvis händer detta inte alltid – armen kan rotera när den rör sig och översätta. Men vi kan se vad som händer genom att hugga upp det svepade området enligt följande:

eftersom mäthjulet är i mitten av armen, när armen roterar, klämmer den de små blocken på ena sidan när den expanderar dem på den andra. Dessa effekter avbryter varandra exakt.
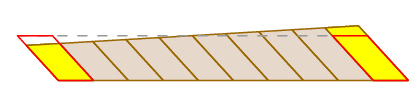
ett fullständigt rigoröst bevis kan ges genom att använda formeln för ändring av variabler i en dubbel integral och uttrycket för hjulresor som en vägintegral.
Antag nu att hjulet är placerat någon annanstans. Säg att dess position är c + v där c är armens mitt och v en vektor längs armen. Längden på v kommer att förbli fast, säg vid XXL. Vägen som hjulet följer är c(t) + v (t). Vägintegralet är nu
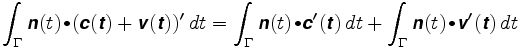
den första integralen är avståndet som hjulet skulle resa om det var i mitten av armen. I det andra är vektorn v(t) alltid vinkelrätt mot n och v(t) har konstant längd. Vektorn v (t) rör sig runt på en cirkel med radie som är lika med XXL. Därför är punktprodukten av n och v'(t) bara den signerade längden på v'(t), och den andra integralen är lika med 20 gånger armens totala rotation. Därför:
om hjulet befinner sig på avstånd från mitten av armen, är avståndet C hjulmåtten C0, avståndet som skulle mätas om hjulet var i mitten, plus att det är flera gånger den totala vinkeln som armen roterar.
Du kan omedelbart se ett enkelt fall av detta genom att rotera armen runt dess centrum. Genom att kombinera detta med Guldins Sats ser vi att i alla fall:
c = C0 + OC i
område sopas ut = l C0 = L C – l OC i
det fullständiga resultatet
guldins formel ger ett signerat område-om du sveper bakåt över ett område går hjulet bakåt och du avbryter område du redan har täckt. Om vi tillämpar detta på fallet där den fria armen kommer tillbaka exakt där den började ser vi att lC är lika med området i det stängda området som spåras ut av armens högra ände minus det i regionen som sveps ut av den vänstra.
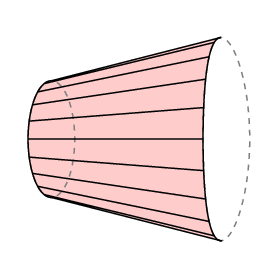

När det gäller den polära planimetern är armens botten begränsad till en båge i radiecirkeln r med centrum vid Polen, varför l C är området spåras ut av spåraren. Dessutom ligger Polen normalt utanför det område som ska mätas, och i detta fall måste armens totala rotation vara 0. Så i det här fallet har vi
area of the region traced = lC
här är figuren som ingår av Jakob Amsler, uppfinnaren, i sitt ursprungliga papper på instrumentet han uppfann:
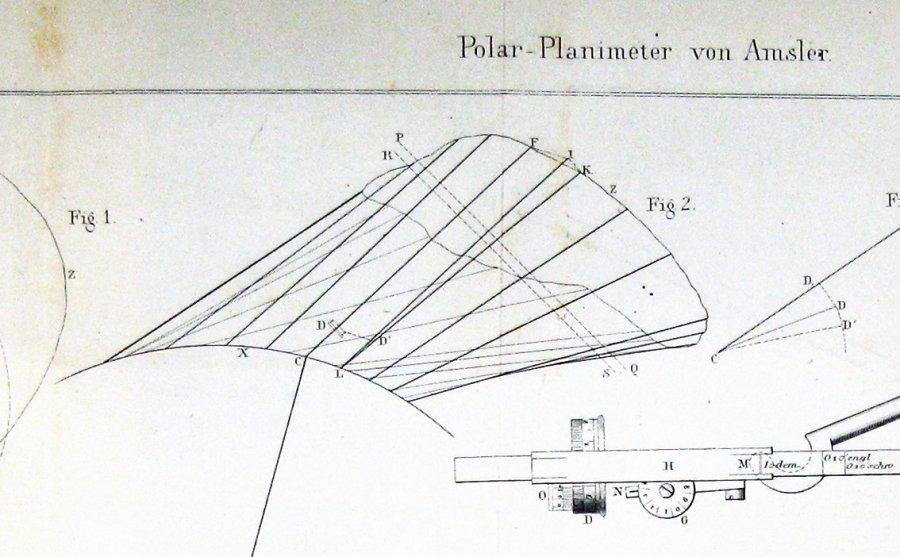
det verkar ganska tydligt av detta att Amsler härledde sin konstruktion genom någon form av Guldins teorem.
Planimetrar och Greens teorem
som vi redan har nämnt, efter att ha valt planimeterns orientering, är planimeterkonfigurationen en kontinuerlig funktion av spårpositionen. Säg att vi väljer den positiva inriktningen. Sedan kan vi fästa vid varje punkt i ringen en enhetsvektor n, den som pekar moturs och vinkelrätt mot spårarmen vid spåraren.
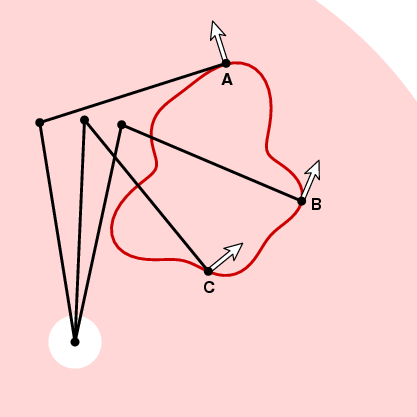
hur mäthjulet kommer att reagera på rörelse längs kurvan i nästa ögonblick beror på vinkeln mellan denna vektor och kurvens tangentvektor. Vid A på bilden ovan kommer mäthjulet inte att röra sig eftersom rörelsen längs kurvan är parallell med spårarmen. Vid B om spåraren flyttar ett litet avstånd ds, så kommer mäthjulet. Och vid C kommer mäthjulet att flytta ett avstånd mellan 0 och ds. För att vara exakt, anta att t är enhetens tangentvektor vid någon punkt i kurvan. Om spåraren flyttar avstånd ds längs kurvan, kommer mäthjulet vid den punkten att flytta ett avstånd d ds, där d = n . t, punktprodukten av enhetsvektorerna t och n. med andra ord, om vi rör oss runt kurvan Bisexuell mäthjulet kommer att flytta ett totalt avstånd lika med integralen av n . t ds (dot product), eller

men eftersom varje punkt i ringen motsvarar en unik positiv konfiguration av planimetern, kan vi tilldela en vektor n till varje inre punkt i ringen, och det definierar därför ett vektorfält. Kurvan är gränsen för dess inre, och enligt en av våra antaganden finns detta helt i den region där n definieras. Greens Sats berättar för oss att vägen integral runt gränsen för denna region också är lika med en viss integral över: Därför
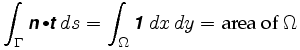
mer exakt berättar Greens sats att
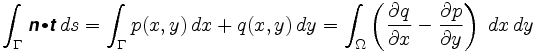
där n = är vektorfältet involverat. Integrand i den dubbla integralen kallas vektorfältets krullning.
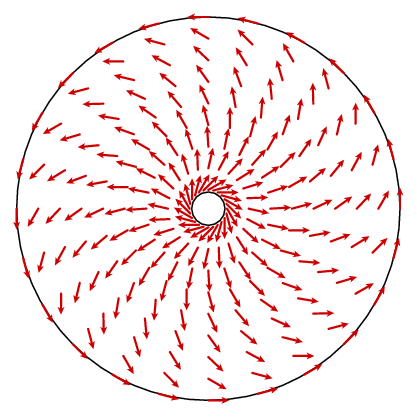
detta verkar inte få oss så långt. Vad som borde hända är att curl är en konstant 1. I princip kunde vi hitta en formel för vektorfältet n och beräkna dess krullning, men det är inte särskilt upplysande. Vi kan dock dra nytta av ett annat faktum. Vektorfältet har cirkulär symmetri, vilket innebär att det bestäms av vad det är på en radie. Cosinuslagen ger oss en enkel formel för den perifera komponenten.
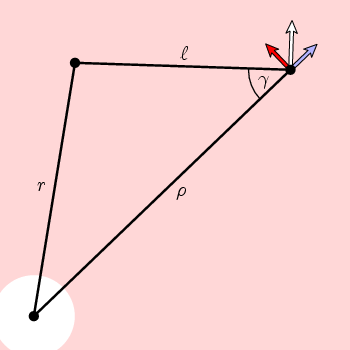
det följer av enkel geometri i denna figur att periferikomponenten i n är
f(kub) = cos(kub) = (2 + 2 + 2 – r 2)/(2 kg l)
den verkliga punkten i Greens sats är att för att verifiera att integandet är 1 räcker det att verifiera att banan är integrerad runt lämplig små stigar är desamma som området. För detta väljer vi våra regioner att vara som här:
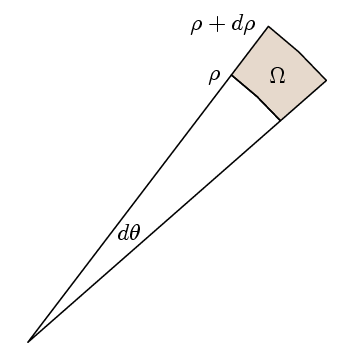
Sedan l gånger path integral är
l (ρ+dp)( f(ρ+dp)- f(ρ) ) dθ
eller
(θ/2) ( (ρ + dp) 2 – ρ 2)
vilket är det område i regionen Ω.
andra typer av planimetrar
Guldins Sats innebär att rörelsen hos ett mäthjul kommer att berätta det område som spåras ut av spåraren när armen med ett mäthjul på det spårar ut en kurva men har en ände begränsad till en endimensionell kurva. Detta händer till exempel med den rullande planimetern, där pivoten är begränsad till en rak linje genom att vara på en rullande cylinder.

för att ta reda på mer
-
 tillverkar och säljer fortfarande planimetrar.
tillverkar och säljer fortfarande planimetrar. - Differential och integrerad kalkyl Volym II, R. Courant, Blackie & Son, 1936. Avsnittet Om Guldins Formel (s. 294-298) ger en förklaring av hur planimetern fungerar.
- Amslers ursprungliga artikel, Vierteljahresschrift der Naturforschenden Gesellschaft i Zuerich, 1856. Detta saknar diagrammen, men de är här:
- Amslers första diagram
- Amslers andra diagram
vårt tack till Donna Sammis Från Stony Brook University Library för att hitta artikeln och till hennes man Robert för att leverera fotografier av figurerna.
företaget som Amsler grundade producerade instrument långt in på 20-talet. Detta fotografi visar logotypen på en strömavtagarversion av planimetern:

- ”Om Planimetrar,” EngineerSupply. Företaget har också lagt upp en video på YouTube.
Bill Casselman
University of British Columbia, Vancouver, Kanada
cass at math.ubc.ca
John Eggers
University of California, San Diego
jeggers at ucsd.edu
de som kan komma åt JSTOR kan hitta några av de papper som nämns ovan där. För dem med tillgång, American Mathematical Society ’ s MathSciNet kan användas för att få ytterligare bibliografisk information och recensioner av vissa dessa material. Några av objekten ovan kan nås via ACM-portalen, som också tillhandahåller bibliografiska tjänster.