i dagens artikel kommer vi att titta på rolling and expanding windows.
i slutet av inlägget kommer du att kunna svara på dessa frågor:
- Vad är ett rullande fönster?
- Vad är ett expanderande fönster?
- Varför är de användbara?
Vad är ett rullande eller expanderande fönster?

här är ett normalt fönster.
vi använder vanliga fönster eftersom vi vill ha en glimt av utsidan, ju större fönstret desto mer av utsidan får vi se.
också som en allmän tumregel, Ju större fönster på någons hus, desto bättre gjorde deras aktieportfölj …
precis som riktiga fönster erbjuder datafönster oss också en liten inblick i något större.
ett rörligt fönster tillåter oss att undersöka en delmängd av våra data.
rullande fönster
ofta vill vi veta en statistisk egenskap av våra tidsseriedata, men eftersom alla tidsmaskiner är låsta i Roswell kan vi inte beräkna en statistik över hela provet och använda det för att få insikt.
det skulle introducera look-ahead bias i vår forskning.
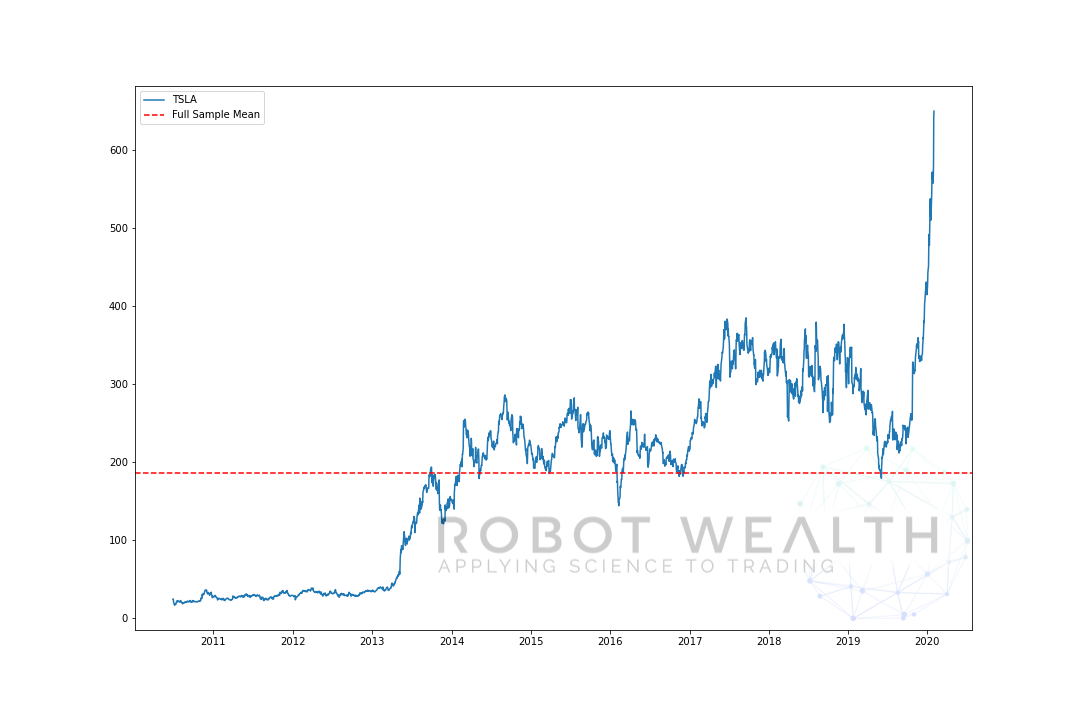
Här är ett extremt exempel på det. Här har vi ritat TSLA-priset och dess medelvärde över hela provet.
import pandas as pdimport matplotlib.pyplot as plt #Load TSLA OHLC df = pd.read_csv('TSLA.csv')#Calculate full sample meanfull_sample_mean = df.mean()#Plotplt.plot(df,label='TSLA')plt.axhline(full_sample_mean,linestyle='--',color='red',label='Full Sample Mean')plt.legend()plt.show()
i det här fallet, om vi bara köpte TSLA när priset var under medelvärdet och sålde det över medelvärdet, skulle vi ha gjort ett dödande, väl åtminstone fram till 2019…
men problemet är att vi inte skulle ha känt medelvärdet vid den punkten i tid.
så det är ganska uppenbart varför vi inte kan använda hela provet, men vad kan vi göra då? Ett sätt vi kan närma oss detta problem är att använda rullande eller expanderande fönster.
om du någonsin har använt ett enkelt glidande medelvärde, så grattis-du har använt ett rullande fönster.
hur fungerar rullande fönster?
låt oss säga att du har 20 dagars lagerdata och du vill veta medelpriset på aktien för de senaste 5 dagarna. Vad gör du?
du tar de senaste 5 dagarna, summerar dem och delar med 5.
men vad händer om du vill veta genomsnittet av de föregående 5 dagarna för varje dag i din datamängd?
det är här rullande fönster kan hjälpa.
i det här fallet skulle vårt fönster ha en storlek på 5, vilket betyder för varje tidpunkt det innehåller medelvärdet av de senaste 5 datapunkterna.
låt oss visualisera ett exempel med ett rörligt fönster i storlek 5 steg för steg.
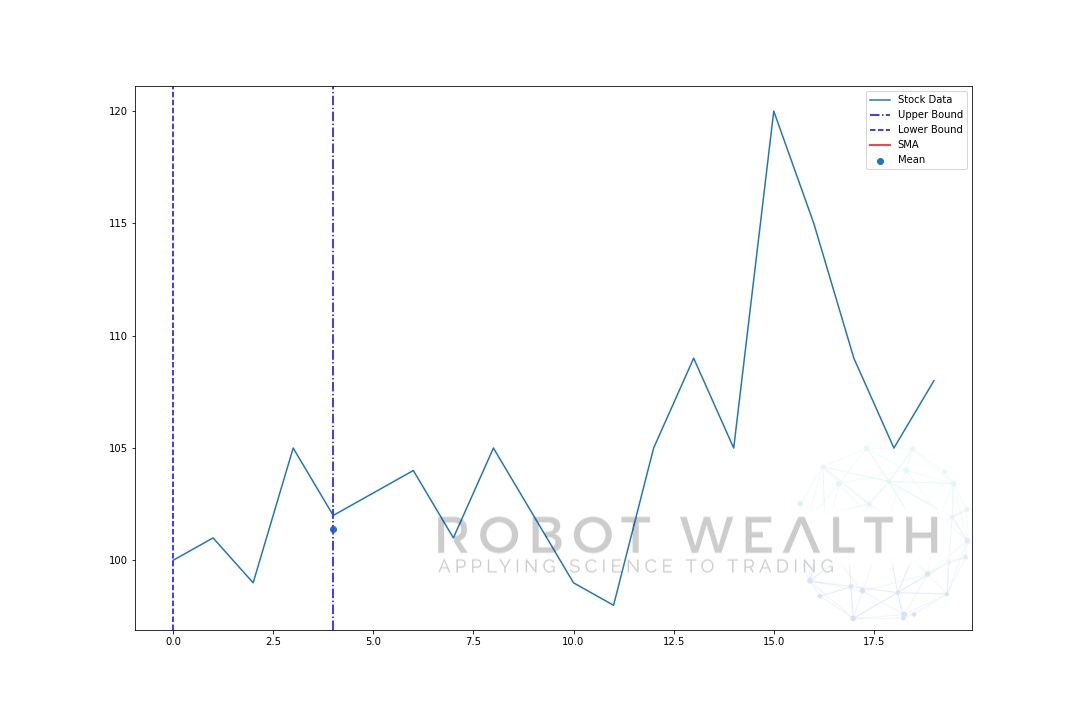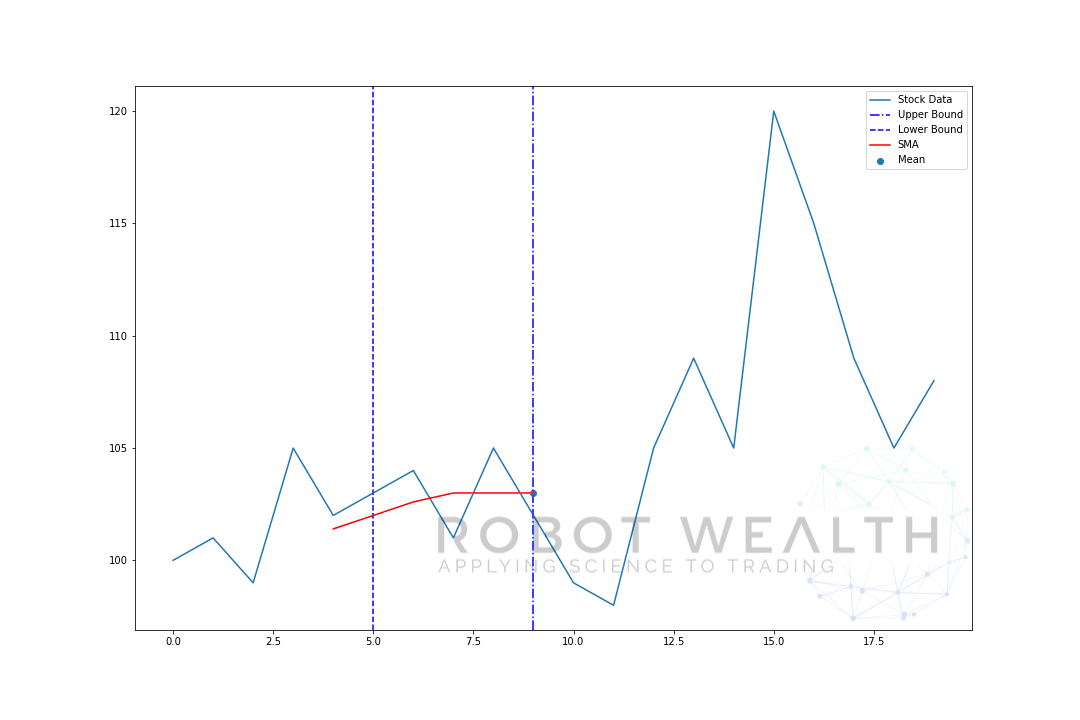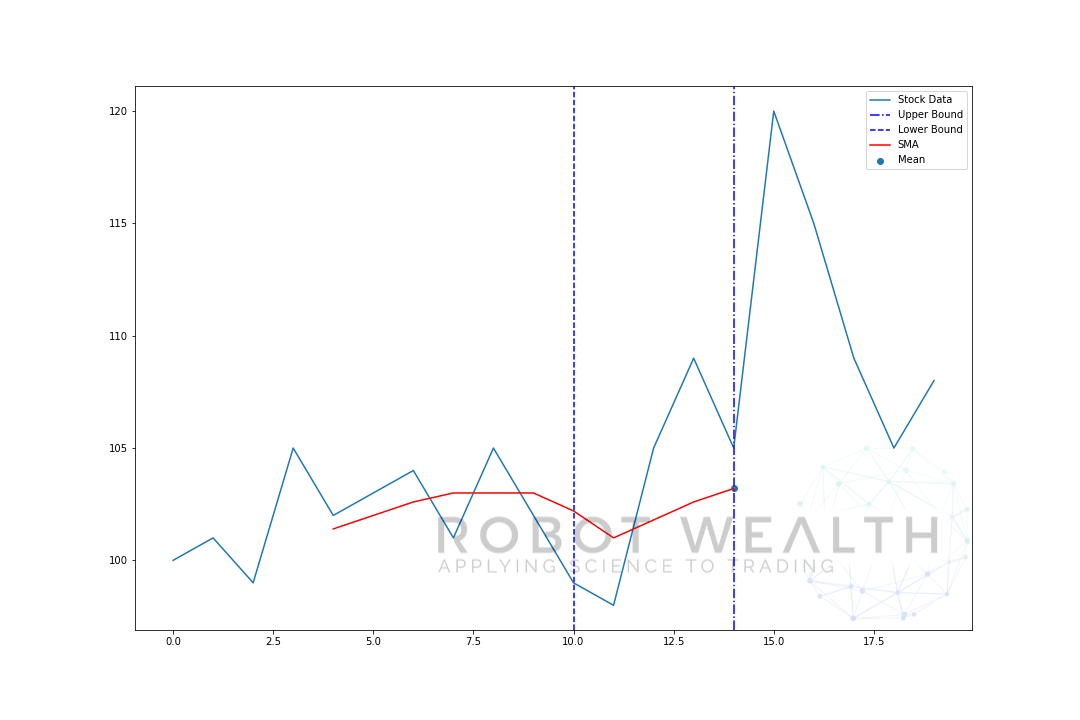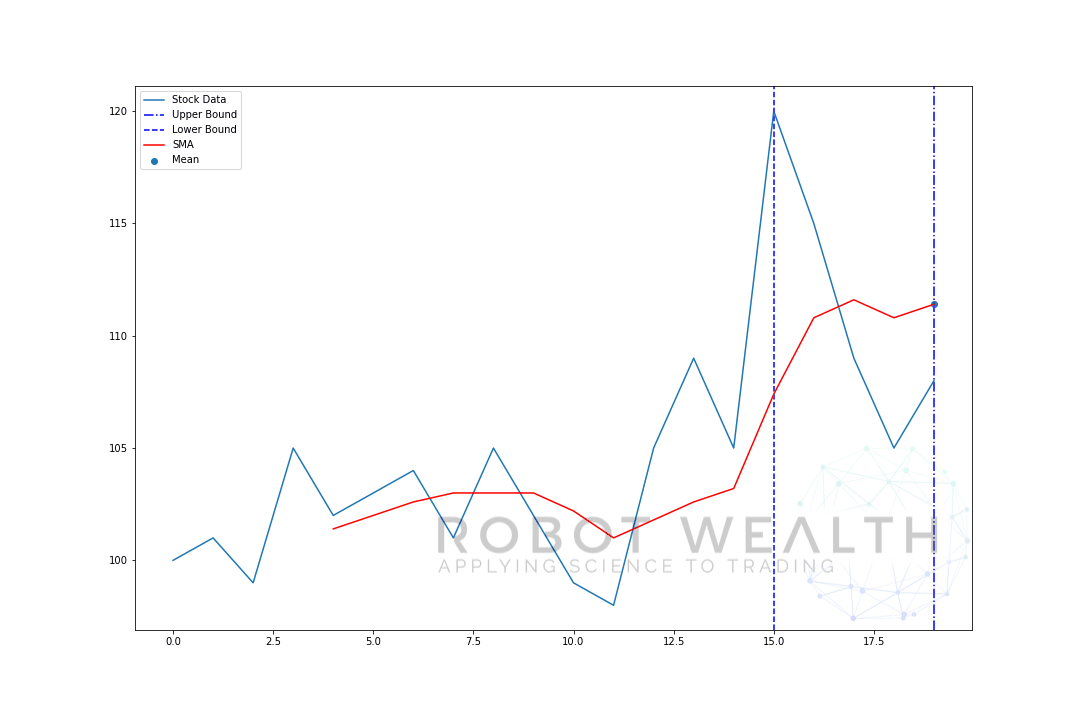
#Random stock pricesdata = #Create pandas DataFrame from listdf = pd.DataFrame(data,columns=)#Calculate a 5 period simple moving averagesma5 = df.rolling(window=5).mean()#Plotplt.plot(df,label='Stock Data')plt.plot(sma5,label='SMA',color='red')plt.legend()plt.show()
så låt oss bryta ner det här diagrammet.
- Vi har 20 dagars aktiekurser i detta diagram, märkta aktiedata.
- för varje tidpunkt (den blå pricken) vill vi veta vad som är 5-dagens medelpris.
- lagerdata som används för beräkningen är sakerna mellan de 2 blå vertikala linjerna.
- när vi beräknar medelvärdet från 0-5 blir vårt medelvärde för dag 5 tillgängligt.
- för att få medelvärdet för dag 6 måste vi flytta fönstret med 1 Så blir datafönstret 1-6.
och detta är vad som kallas ett rullande fönster, storleken på fönstret är fast. Allt vi gör är att rulla det framåt.
som du säkert har märkt har vi inte SMA-värden för punkterna 0-4. Detta beror på att vår fönsterstorlek (även känd som en lookback-period) kräver minst 5 datapunkter för att göra beräkningen.
expanderande fönster
där rullande fönster är en fast storlek, har expanderande fönster en fast utgångspunkt och innehåller nya data när de blir tillgängliga.
Så här tycker jag om att tänka på det här:
” vad är medelvärdet av de senaste n-värdena vid denna tidpunkt?”- Använd rullande fönster här.
” vad är medelvärdet av all tillgänglig data fram till denna tidpunkt?”- Använd expanderande fönster här.
expanderande fönster har en fast nedre gräns. Endast fönstrets övre gräns rullas framåt (fönstret blir större).
låt oss visualisera ett expanderande fönster med samma data från föregående plot.
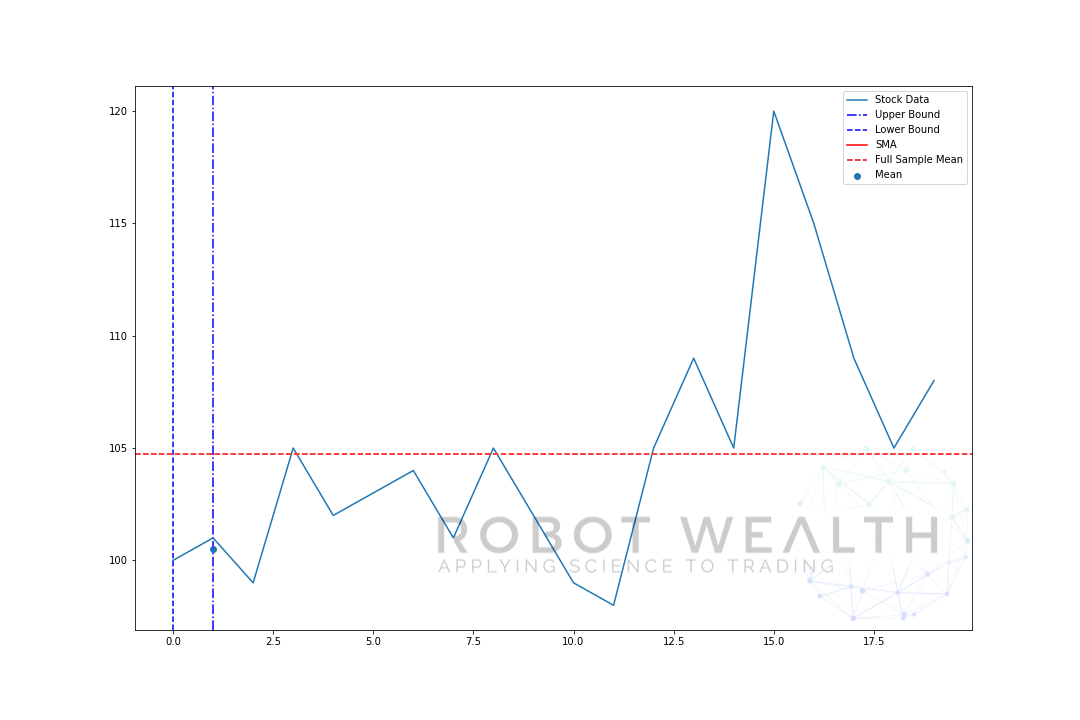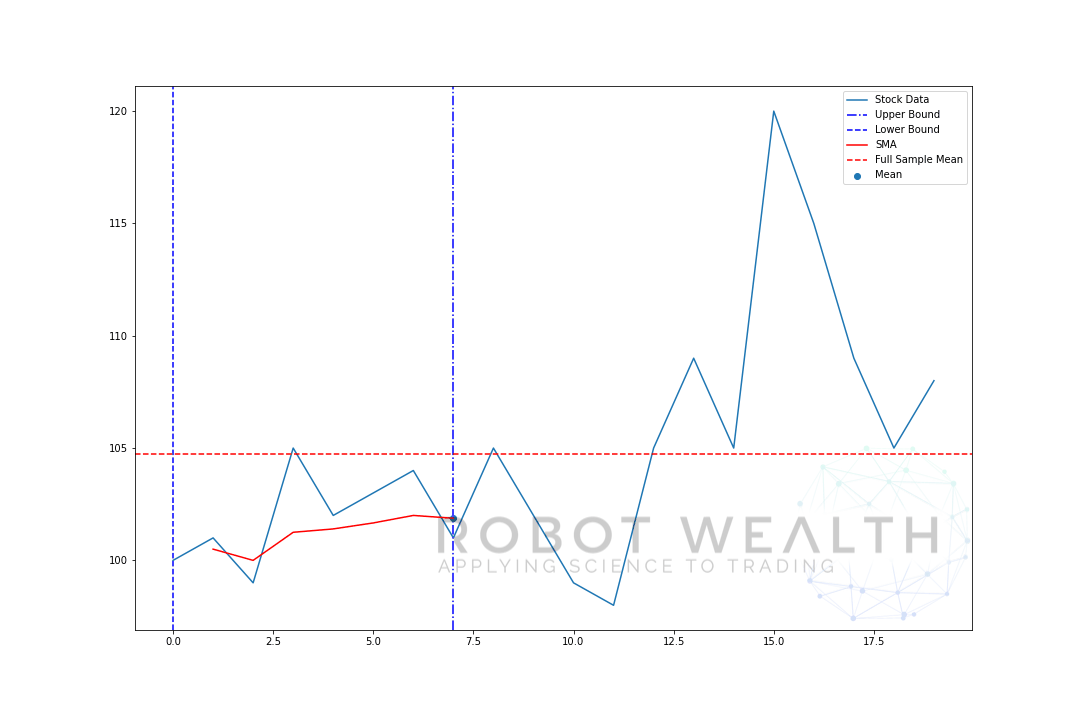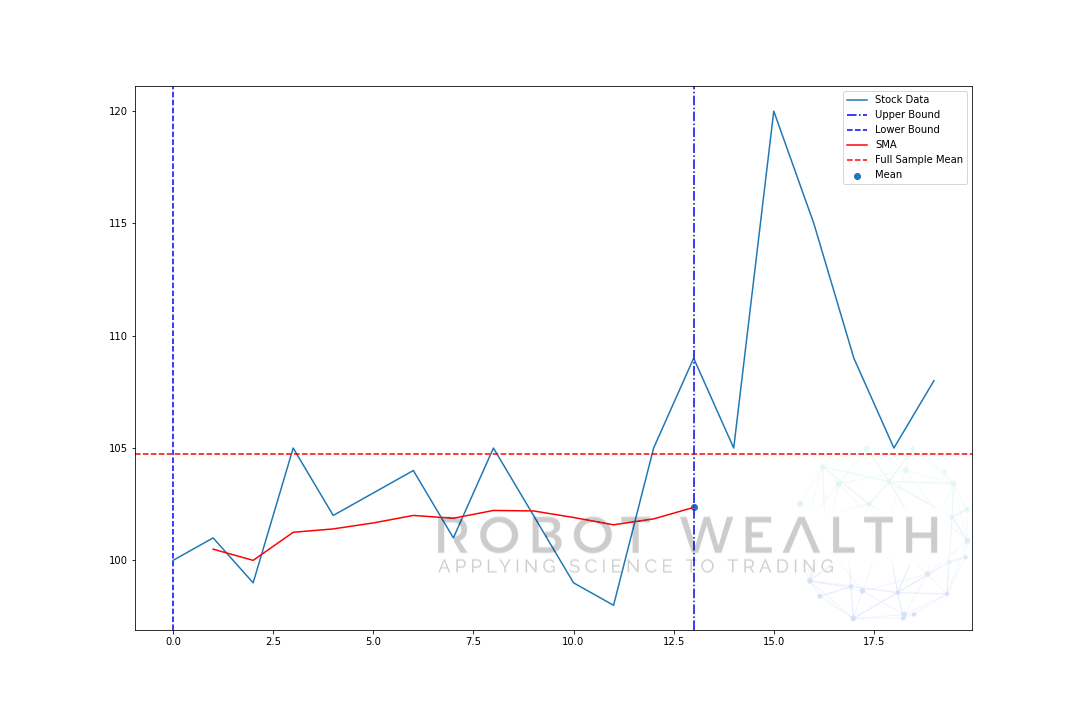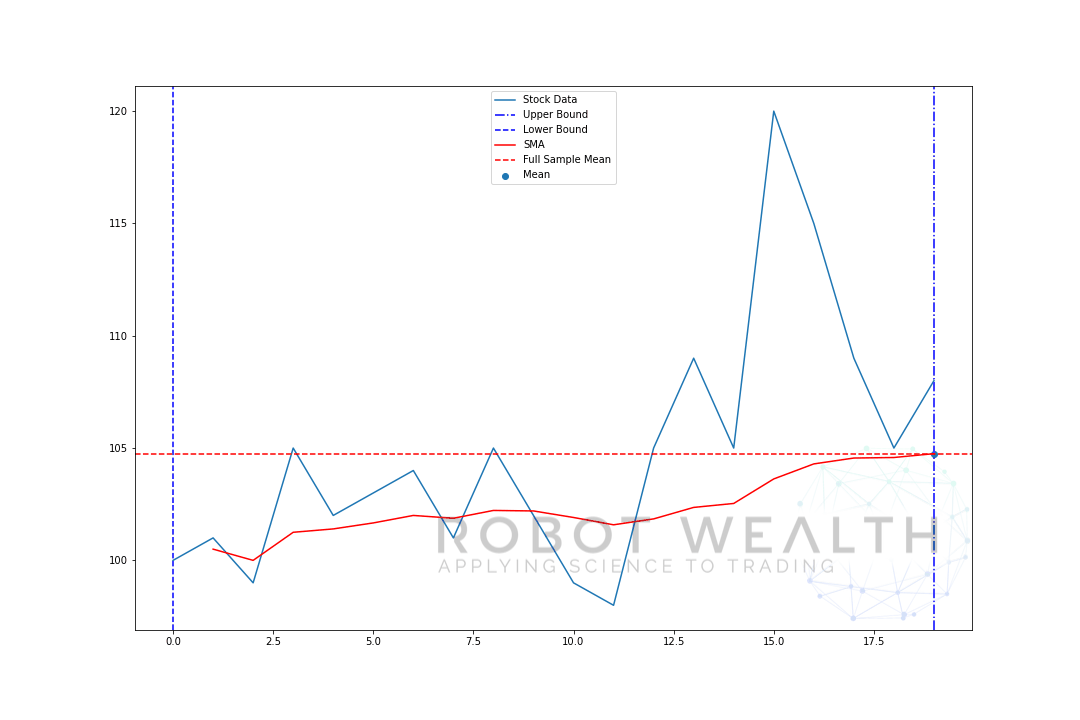
#Random stock prices data = #Create pandas DataFrame from list df = pd.DataFrame(data,columns=) #Calculate expanding window meanexpanding_mean = df.expanding(min_periods=1).mean()#Calculate full sample mean for referencefull_sample_mean = df.mean()#Plot plt.plot(df,label='Stock Data') plt.plot(expanding_mean,label='Expanding Mean',color='red')plt.axhline(full_sample_mean,label='Full Sample Mean',linestyle='--',color='red')plt.legend()plt.show()
Du kan se att SMA i början är lite jittery. Det beror på att vi har ett mindre antal datapunkter i början av tomten, och när vi får mer data expanderar fönstret tills så småningom konvergerar det expanderande fönstermedlet till hela provmedlet, eftersom fönstret har nått storleken på hela datasatsen.
sammanfattning
det är viktigt att inte använda data från framtiden för att analysera det förflutna. Rullande och expanderande fönster är viktiga verktyg för att hjälpa ”gå dina data framåt” för att undvika dessa problem.
om du gillade det här kommer du förmodligen att gilla dessa också…
finansiell data Manipulation i dplyr för Quant Traders
använda Digital signalbehandling i kvantitativa handelsstrategier
backtesting bias: känns bra tills du blåser upp