introduktion
Principal Components Analysis (PCA) är en dimensionalitetsreduceringsalgoritm som kan användas för att påskynda din oövervakade funktionsinlärningsalgoritm avsevärt. Ännu viktigare är att förstå PCA gör det möjligt för oss att senare implementera blekning, vilket är ett viktigt förbehandlingssteg för många algoritmer.
anta att du tränar din algoritm på bilder. Då kommer ingången att vara något överflödig, eftersom värdena för intilliggande pixlar i en bild är starkt korrelerade. Konkret antar vi att vi tränar på 16×16 gråskalebildplåster. Då är\textstyle x \in \Re^{256} 256 dimensionella vektorer, med en funktion \textstyle x_j som motsvarar intensiteten för varje pixel. På grund av korrelationen mellan intilliggande pixlar tillåter PCA oss att approximera ingången med en mycket lägre dimensionell, samtidigt som det uppstår mycket litet fel.
exempel och matematisk bakgrund
för vårt löpande exempel använder vi en dataset \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} med \textstyle n=2 dimensionella ingångar, så att \textstyle x^{(i)} \in \Re^2. Antag att vi vill minska data från 2 dimensioner till 1. (I praktiken kanske vi vill minska data från 256 till 50 dimensioner, säg; men med hjälp av lägre dimensionella data i vårt exempel kan vi visualisera algoritmerna bättre.) Här är vår dataset:
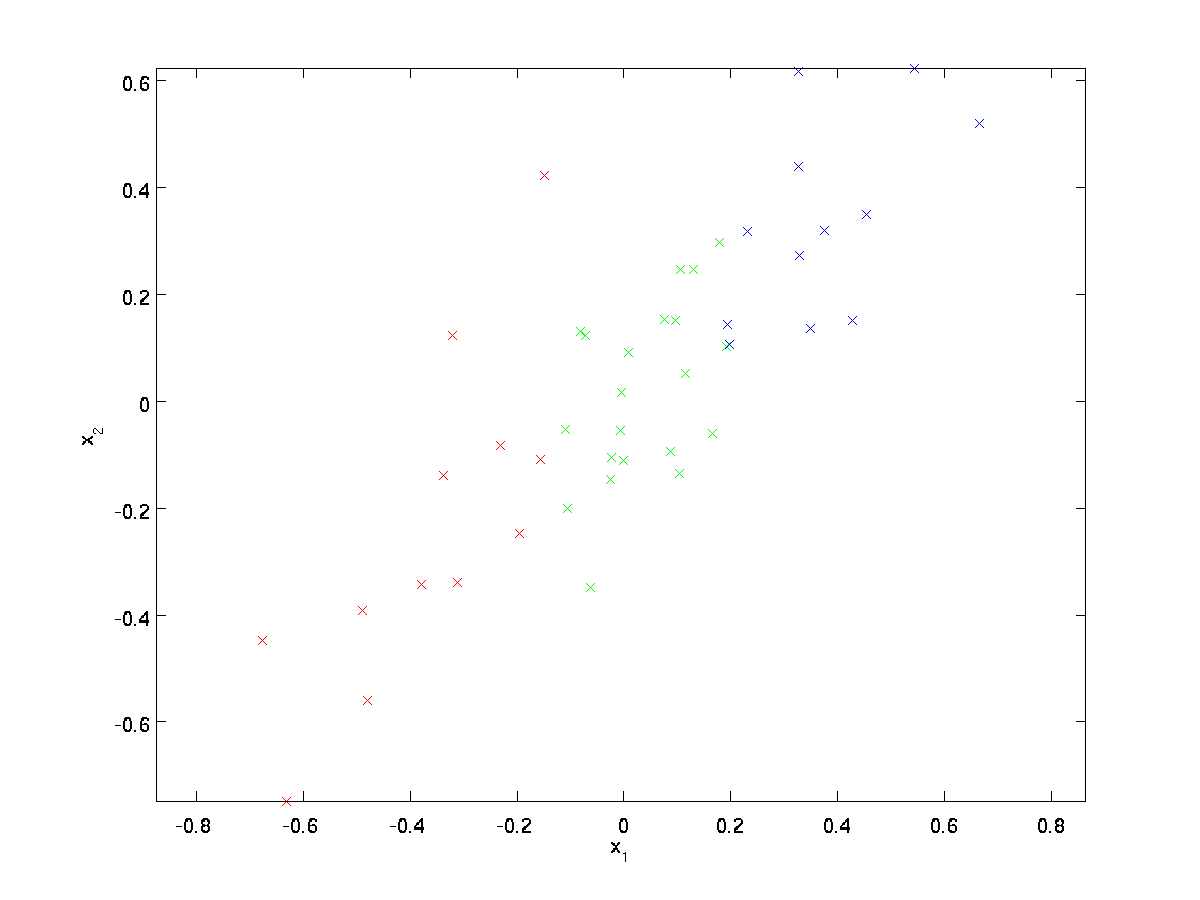
dessa data har redan förbehandlats så att var och en av funktionerna \textstyle x_1 och \textstyle x_2 har ungefär samma medelvärde (noll) och varians.
för illustrationens syfte har vi också färgat var och en av punkterna en av tre färger, beroende på deras \ textstyle x_1-värde; dessa färger används inte av algoritmen, och är endast för illustration.
PCA kommer att hitta ett lägre dimensionellt underrum för att projicera våra data.
från att visuellt undersöka data verkar det som om \textstyle u_1 är den huvudsakliga variationsriktningen för data, och \textstyle u_2 den sekundära variationsriktningen:
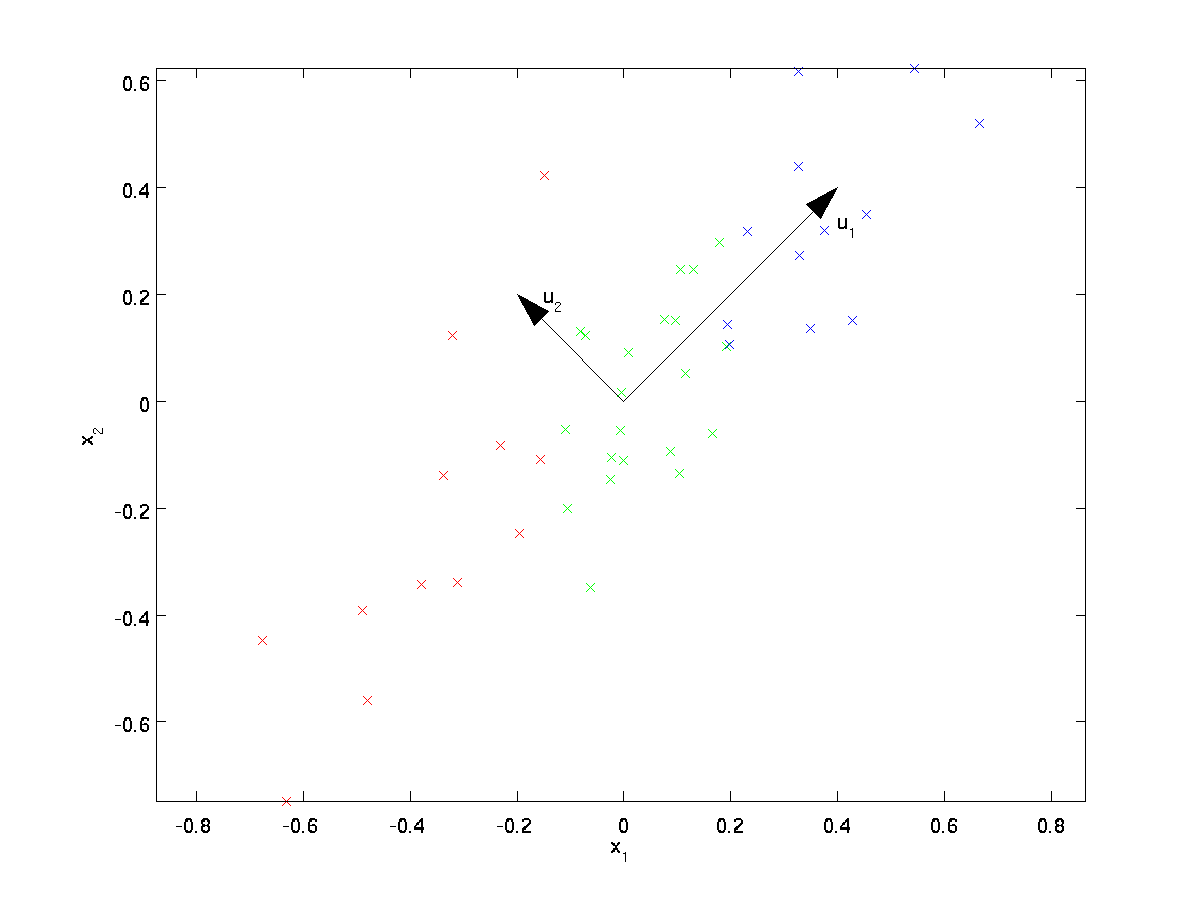
dvs, data varierar mycket mer i riktningen \textstyle u_1 än \textstyle u_2. För att mer formellt hitta anvisningarna \textstyle u_1 och \textstyle u_2 beräknar vi först matrisen \ textstyle \ Sigma enligt följande:
\ begin{align} \ Sigma = \ frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \end{align}
om \textstyle x har noll medelvärde, är \textstyle \Sigma exakt kovariansmatrisen för \textstyle x. (symbolen ”\textstyle \Sigma”, uttalad ”Sigma”, är standardnotationen för att beteckna kovariansmatrisen. Tyvärr ser det ut som summeringssymbolen, som i \ sum_{i=1}^n i; men det här är två olika saker.)
det kan sedan visas att \textstyle u_1—den huvudsakliga variationsriktningen för data-är den övre (huvudsakliga) egenvektorn för \textstyle \Sigma, och \textstyle u_2 är den andra egenvektorn.
Obs: Om du är intresserad av att se en mer formell matematisk härledning/motivering av detta resultat, se cs229 (maskininlärning) föreläsningsanteckningar på PCA (länk längst ner på denna sida). Du behöver dock inte göra det för att följa den här kursen.
Du kan använda standard numerisk linjär algebra programvara för att hitta dessa egenvektorer (se Implementeringsanvisningar). Låt oss konkret beräkna egenvektorerna av \ textstyle \ Sigma och stapla egenvektorerna i kolumner för att bilda matrisen \ textstyle U:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.
vektorerna \ textstyle u_1 och \textstyle u_2 i vårt exempel utgör en ny grund där vi kan representera data. Konkret, låt \textstyle x \ in \ Re^2 vara ett träningsexempel. Då är \ textstyle u_1^Tx längden (storleken) på projektionen av \textstyle x på vektorn \textstyle u_1.
På samma sätt är \textstyle u_2^Tx storleken på \textstyle x projicerad på vektorn \ textstyle u_2.
rotera Data
Således kan vi representera \textstyle x i \textstyle (u_1, u_2)-basis genom att beräkna
\begin{align}x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}
(prenumerationen ”rot” kommer från observationen att detta motsvarar en rotation (och eventuellt reflektion) av den ursprungliga uppgifter.) Låt oss ta hela träningsuppsättningen och beräkna \textstyle x_ {\rm rot}^{(i)} = U^Tx^{(i)} för varje \ textstyle i. plotta denna transformerade data \ textstyle x_ {\rm rot}, vi får:

detta är träningsuppsättningen roterad i \textstyle u_1,\textstyle u_2-basen. I det allmänna fallet kommer \ textstyle U^Tx att vara träningsuppsättningen roterad till basen \textstyle u_1,\textstyle u_2,…, \ textstyle u_n.
en av egenskaperna hos \textstyle U är att det är en” ortogonal ” matris, vilket innebär att den uppfyller \textstyle U^TU = UU^T = I. Så om du någonsin behöver gå från de roterade vektorerna \textstyle x_{\rm rot} tillbaka till originaldata \textstyle x, kan du beräkna
\begin{align}x = U x_{\rm rot} ,\end{align}
eftersom \textstyle U x_{\RM rot} = UU^t x = x.
minska Datadimensionen
Vi ser att den huvudsakliga variationsriktningen för data är den första dimensionen \textstyle x_{\RM rot,1} av denna roterade data. Således, om vi vill minska dessa data till en dimension, kan vi ställa in
\begin{align}\tilde{x}^{(i)} = x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} \in \Re.\end{align}
Mer Allmänt, om \textstyle x \ in \ Re^n och vi vill minska den till en \ textstyle k dimensionell representation \textstyle \tilde{x} \in \re^k (där k < n), skulle vi ta de första \textstyle k-komponenterna i \textstyle x_{\rm rot}, som motsvarar de översta \textstyle k-riktningarna för variation.
ett annat sätt att förklara PCA är att \ textstyle x_ {\rm rot} är en \ textstyle n dimensionell vektor, där de första komponenterna sannolikt kommer att vara stora (t. ex., i vårt exempel såg vi att \textstyle x_ {\rm rot, 1}^{(i)} = u_1^Tx^{(i)} Tar rimligt stora värden för de flesta exempel \textstyle i), och de senare komponenterna kommer sannolikt att vara små (t.ex. i vårt exempel, \textstyle x_{\rm rot, 2}^{(i)} = u_2^Tx^{(i)} var mer benägna att vara små). Vad PCA gör det det släpper de senare (mindre) komponenterna i \textstyle x_{\rm rot}, och approximerar dem bara med 0 ’ S. konkret kan vår definition av \textstyle \tilde{x} också nås med hjälp av en approximation till \textstyle x_{\rm rot} där alla utom de första \textstyle k-komponenterna är nollor. Med andra ord har vi:
\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rot, 1} \\\vdots \\ x_{\rm rot,k} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\ca \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\RM rot,k} \\x_{\rm rot,k+1} \\\vdots \\ x_{\rm rot,n} \end{bmatrix}= x_{\RM rot} \end{align}
i vårt exempel ger detta oss följande plot av \textstyle \tilde{X} (med \textstyle n=2,K=1):

eftersom de slutliga \textstyle n-k-komponenterna i \textstyle \tilde{x} enligt definitionen ovan alltid skulle vara noll, behöver vi inte hålla dessa nollor runt, och så definierar vi \textstyle \tilde{x} som en \textstyle k-dimensionell vektor med bara de första \textstyle k (icke-noll) komponenterna.
detta förklarar också varför vi ville uttrycka våra data i \textstyle u_1, u_2, \ ldots, u_n basis: att bestämma vilka komponenter som ska behållas blir bara att hålla de bästa \textstyle k-komponenterna. När vi gör detta säger vi också att vi ”behåller de bästa \textstyle k PCA (eller huvudkomponenter).”
återställa en Approximation av Data
Nu är \textstyle \ tilde{x} \ in \ Re^k en lägre dimensionell,” komprimerad ” representation av den ursprungliga \textstyle x \in \Re^n. givet \textstyle \tilde{x}, Hur kan vi återställa en approximation \textstyle \hat{x} till det ursprungliga värdet av \textstyle x? Från ett tidigare avsnitt vet vi att \textstyle x = U x_ {\rm rot}. Vidare kan vi tänka på \textstyle \ tilde{x} som en approximation till \textstyle x_ {\rm rot}, där vi har satt de sista \textstyle nk-komponenterna till nollor. Således, med tanke på \textstyle \tilde{x} \in \Re^k, kan vi padda ut det med \textstyle n-k nollor för att få vår approximation till \textstyle x_{\rm rot} \in \Re^n. slutligen multiplicerar vi med \textstyle U för att få vår approximation till \textstyle x. konkret får vi
\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{X}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^K u_i \Tilde{X}_i. \ end{align}
den slutliga likheten ovan kommer från definitionen av \textstyle U ges tidigare. (I en praktisk implementering skulle vi faktiskt inte noll pad \ textstyle \ tilde{x} och multiplicera sedan med \ textstyle U, eftersom det skulle innebära att man multiplicerar många saker med nollor; istället skulle vi bara multiplicera \textstyle \tilde{x} \i \Re^k med de första \textstyle k-kolumnerna i \textstyle U som i det slutliga uttrycket ovan.) Genom att tillämpa detta på vår dataset får vi följande plot för \textstyle \ hat{x}:
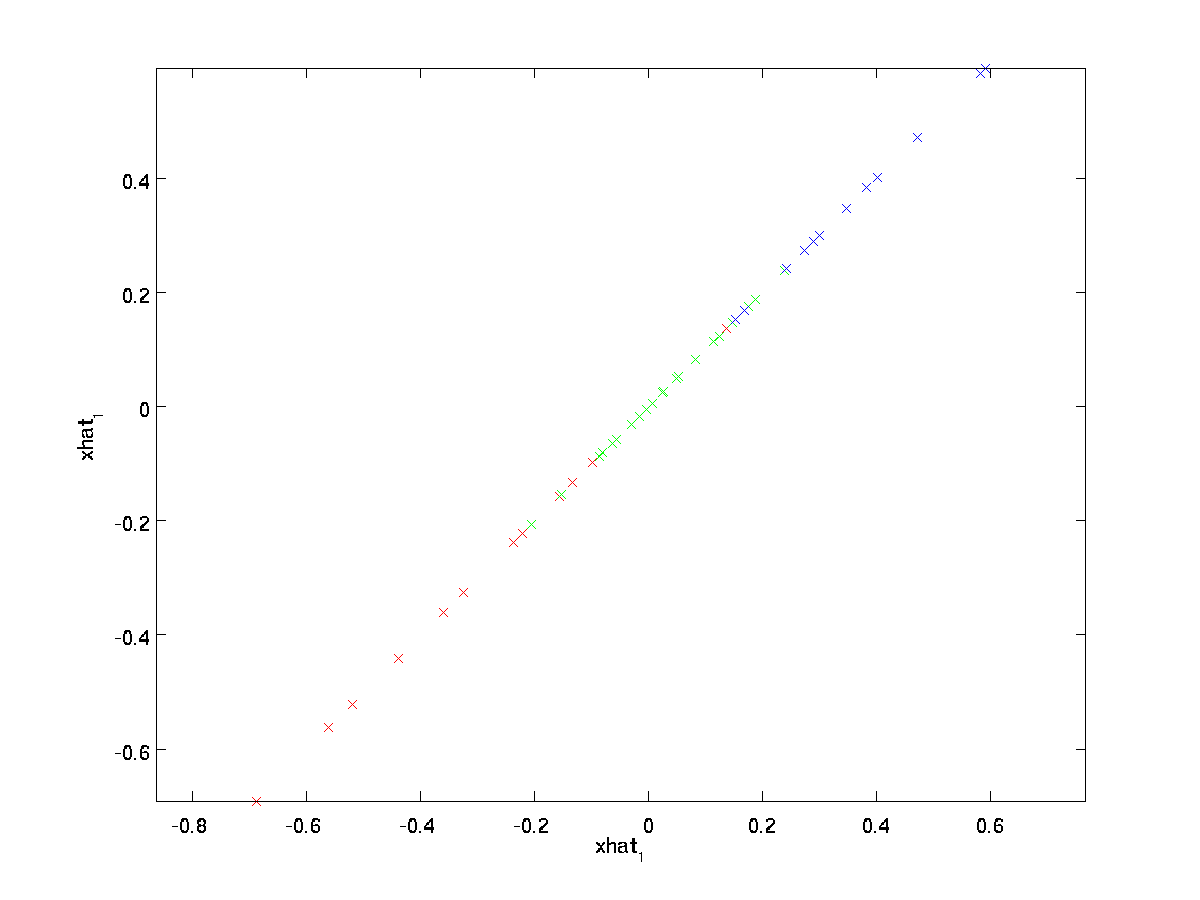
vi använder således en 1-dimensionell approximation till den ursprungliga datasatsen.
om du tränar en autoencoder eller annan oövervakad funktionsinlärningsalgoritm beror körtiden för din algoritm på inmatningens dimension. Om du matar \textstyle \ tilde{x} \ in \ Re^k i din inlärningsalgoritm istället för \textstyle x, kommer du att träna på en lägre dimensionell ingång, och därmed kan din algoritm springa betydligt snabbare. För många datamängder kan den lägre dimensionella \textstyle \tilde{x} – representationen vara en extremt bra approximation till originalet, och att använda PCA på detta sätt kan påskynda din algoritm avsevärt medan du introducerar mycket litet approximationsfel.
antal komponenter att behålla
hur ställer vi in \textstyle k; dvs hur många PCA-komponenter ska vi behålla? I vårt enkla 2-dimensionella exempel verkade det naturligt att behålla 1 av 2-komponenterna, men för högre dimensionella data är detta beslut mindre trivialt. Om \textstyle k är för stor, kommer vi inte att komprimera data mycket; i gränsen för \textstyle k=n, använder vi bara originaldata (men roteras till en annan grund). Omvänt, om \textstyle k är för liten, kan vi använda en mycket dålig approximation till data.
för att bestämma hur man ställer in \ textstyle k, kommer vi vanligtvis att titta på”’ procentuell varians behålls ”’ för olika värden på \textstyle k. konkret, om \textstyle k=n, då har vi en exakt approximation till data, och vi säger att 100% av variansen behålls. Dvs., behålls all variation av originaldata. Omvänt, om \textstyle k=0, då approximerar vi alla data med nollvektorn, och sålunda behålls 0% av variansen.
Mer Allmänt, låt \ textstyle \ lambda_1, \lambda_2, \ldots, \lambda_n vara egenvärdena för \textstyle \ Sigma (sorterad i minskande ordning), så att \textstyle \lambda_j är egenvärdet som motsvarar egenvektorn \ textstyle u_j. om vi behåller \ textstyle k-huvudkomponenterna anges den procentuella variansen som behålls av:
\ begin{align} \ frac {\sum_{j = 1}^k \lambda_j}{\sum_{j=1}^n \lambda_j}.\ end{align}
i vårt enkla 2D-exempel ovan, \textstyle \ lambda_1 = 7.29 och \textstyle \ lambda_2 = 0.69. Genom att bara behålla \textstyle k=1 huvudkomponenter behöll vi \textstyle 7.29/(7.29+0.69) = 0.913, eller 91,3% av variansen.
en mer formell definition av procentuell varians som behålls ligger utanför ramen för dessa anteckningar. Det är dock möjligt att visa att \textstyle \ lambda_j = \ sum_{i=1}^m x_{\rm rot,j}^2. Således, om \textstyle \lambda_j \ca 0, som visar att \textstyle x_ {\rm rot, j} är vanligtvis nära 0 ändå, och vi förlorar relativt lite genom att approximera den med en konstant 0. Detta förklarar också varför vi behåller de övre huvudkomponenterna (motsvarande de större värdena för \textstyle \lambda_j) istället för de nedre. De översta huvudkomponenterna \ textstyle x_ {\rm rot, j} är de som är mer variabla och som tar större värden, och för vilka vi skulle få ett större approximationsfel om vi skulle ställa dem till noll.
När det gäller bilder är en vanlig heuristisk att välja \textstyle k för att behålla 99% av variansen. Med andra ord väljer vi det minsta värdet av \textstyle k som uppfyller
\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0,99. \end{align}
beroende på applikationen, om du är villig att ådra dig ytterligare fel, används också värden i intervallet 90-98% ibland. När du beskriver för andra hur du tillämpade PCA, säger att du valde \ textstyle k för att behålla 95% av variansen kommer också att vara en mycket lättare tolkningsbar beskrivning än att säga att du behöll 120 (eller vad som helst annat antal) komponenter.
PCA på bilder
för att PCA ska fungera vill vi vanligtvis att alla funktioner \ textstyle x_1, x_2, \ldots, x_n ska ha ett liknande värdeområde som de andra (och ha ett medelvärde nära noll). Om du har använt PCA på andra applikationer tidigare kan du därför ha förbehandlat varje funktion separat för att ha noll medelvärde och enhetsvarians, genom att separat uppskatta medelvärdet och variansen för varje funktion \textstyle x_j. detta är dock inte den förbehandling som vi kommer att tillämpa på de flesta typer av bilder. Antag specifikt att vi tränar vår algoritm på ”’naturliga bilder”’, så att \textstyle x_j är värdet av pixel \textstyle j. med” naturliga bilder ” menar vi informellt vilken typ av bild som ett typiskt djur eller en person kan se under sin livstid.
notera: Vanligtvis använder vi bilder av utomhusscener med gräs, träd etc., och klipp ut små (säg 16×16) bildplåster slumpmässigt från dessa för att träna algoritmen. Men i praktiken är de flesta inlärningsalgoritmer extremt robusta för den exakta typen av bild som den är utbildad på, så de flesta bilder som tagits med en vanlig kamera, så länge de inte är alltför suddiga eller har konstiga artefakter, borde fungera.
När du tränar på naturliga bilder är det lite meningsfullt att uppskatta ett separat medelvärde och varians för varje pixel, eftersom statistiken i en del av bilden (teoretiskt) ska vara densamma som alla andra.
denna egenskap av bilder kallas ”’ stationarity.”’
i detalj, för att PCA ska fungera bra, kräver vi informellt att (i) funktionerna har ungefär nollmedelvärde och (ii) de olika funktionerna har liknande avvikelser till varandra. Med naturliga bilder är (ii) redan nöjd även utan variansnormalisering, och så kommer vi inte att utföra någon variansnormalisering.
(om du tränar på ljuddata-säg, på spektrogram-eller på textdata-säg, bag-of-word vektorer-vi brukar inte utföra varians normalisering antingen.)
i själva verket är PCA invariant till skalning av data, och kommer att returnera samma egenvektorer oavsett skalning av ingången. Mer formellt, om du multiplicerar varje funktionsvektor \ textstyle x med något positivt tal (så skalar varje funktion i varje träningsexempel med samma nummer), kommer PCA: s utgångsegenvektorer inte att ändras.
Så, vi kommer inte att använda varians normalisering. Den enda normaliseringen vi behöver utföra då är genomsnittlig normalisering, för att säkerställa att funktionerna har ett medelvärde runt noll. Beroende på applikationen är vi ofta inte intresserade av hur ljus den övergripande inmatningsbilden är. Till exempel i objektigenkänningsuppgifter påverkar bildens totala ljusstyrka inte vilka objekt som finns i bilden. Mer formellt är vi inte intresserade av medelintensitetsvärdet för en bildplåster; således kan vi subtrahera detta värde som en form av medelnormalisering.
konkret, om \textstyle x^{(i)} \in \Re^{n} är (gråskala) intensitetsvärden för en 16×16 bild patch (\textstyle n=256), kan vi normalisera intensiteten för varje bild \textstyle x^{(i)} enligt följande:
\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_jx^{(i)}_j := X^{(i)}_j – \mu^{(i)}
för alla \textstyle j
Observera att de två stegen ovan görs separat för varje bild \textstyle x^{(i)}, och att \textstyle \mu^{(i)} här är medelintensiteten för bilden \textstyle x^{(i)}. I synnerhet är detta inte samma sak som att uppskatta ett medelvärde separat för varje pixel \textstyle x_j.
om du tränar din algoritm på andra bilder än naturliga bilder (till exempel bilder av handskrivna tecken eller bilder av enstaka isolerade objekt centrerade mot en vit bakgrund) kan andra typer av normalisering vara värda att överväga, och det bästa valet kan vara applikationsberoende. Men när man tränar på naturliga bilder skulle det vara en rimlig standard att använda per-image-normaliseringsmetoden som anges i ekvationerna ovan.
vitare
Vi har använt PCA för att minska dimensionen av data. Det finns ett närbesläktat förbehandlingssteg som kallas vitare (eller, i vissa andra litteraturer, sfärering) som behövs för vissa algoritmer. Om vi tränar på bilder är raw-ingången överflödig, eftersom intilliggande pixelvärden är mycket korrelerade. Målet med blekning är att göra ingången mindre överflödig; mer formellt är vår desiderata att våra inlärningsalgoritmer ser en träningsinmatning där (i) funktionerna är mindre korrelerade med varandra, och (ii) funktionerna har alla samma varians.
2D-exempel
Vi kommer först att beskriva blekning med vårt tidigare 2D-exempel. Vi kommer då att beskriva hur detta kan kombineras med utjämning, och slutligen hur man kombinerar detta med PCA.
hur kan vi göra våra inmatningsfunktioner okorrelerade med varandra? Vi hade redan gjort detta när vi beräknade \ textstyle x_ {\rm rot}^{(i)} = U^Tx^{(i)}.
upprepa vår tidigare figur, vår plot för \textstyle x_{\rm rot} var:

kovariansmatrisen för dessa data ges av:
\begin{align}\begin{bmatrix}7.29 && 0,69\slut{bmatrix}.\ end{align}
(notera: Tekniskt sett kommer många av uttalandena i detta avsnitt om ”kovariansen” att vara sanna endast om data har nollmedelvärde. I resten av detta avsnitt kommer vi att ta detta antagande som implicit i våra uttalanden. Men även om datans medelvärde inte är exakt noll, är intuitionerna vi presenterar här fortfarande sanna, och så är det inte något du borde oroa dig för.)
det är ingen slump att de diagonala värdena är \textstyle \ lambda_1 och \textstyle \lambda_2. Vidare är de diagonala inmatningarna noll; således är \ textstyle x_ {\rm rot, 1} och \textstyle x_{\rm rot,2} okorrelerade och uppfyller en av våra desiderata för vitnade data (att funktionerna är mindre korrelerade).
för att få alla våra inmatningsfunktioner att ha enhetsvarians kan vi helt enkelt skala om varje funktion \textstyle x_{\rm rot,i} med \textstyle 1/\sqrt{\lambda_i}. Konkret definierar vi vår vitnade data \ textstyle x_ {\rm PCAwhite} \ in \ Re^n enligt följande:
\begin{align}x_ {\rm PCAwhite, i} = \ frac{x_ {\rm rot, i} }{\sqrt{\lambda_i}}. \ end{align}
Plotting \textstyle x_ {\rm PCAwhite}, vi får:

dessa data har nu kovarians lika med identitetsmatrisen \textstyle I. vi säger att \textstyle x_{\rm PCAwhite} är vår PCA-vitare version av data: de olika komponenterna i \textstyle x_{\rm PCAwhite} är okorrelerade och har enhetsvarians.
vitare i kombination med dimensioneringsreduktion. Om du vill ha data som är vitare och som är lägre dimensionell än den ursprungliga ingången, kan du också välja att bara behålla de översta \textstyle k-komponenterna i \textstyle x_{\rm PCAwhite}. När vi kombinerar PCA-blekning med regularisering (beskrivs senare) kommer de sista komponenterna i \textstyle x_{\rm PCAwhite} att vara nästan noll ändå och kan därmed säkert släppas.
ZCA Whitening
slutligen visar det sig att det här sättet att få data att ha kovariansidentitet \textstyle I inte är unikt. Konkret, om \textstyle R är någon ortogonal matris, så att den uppfyller \textstyle RR^T = R^TR = i (mindre formellt, om \textstyle R är en rotation/reflektionsmatris), då \textstyle R\, x_{\rm PCAwhite} kommer också att ha identitetskovarians.
i ZCA whitening väljer vi \textstyle R = U. vi definierar
\begin{align}x_{\rm ZCAwhite} = U x_{\rm PCAwhite}\end{align}
Plotting \textstyle x_{\rm ZCAwhite}, vi får:

det kan visas att av alla möjliga val för \textstyle r, detta val av rotation orsakar \textstyle x_{\rm zcawhite} att vara så nära som möjligt till den ursprungliga indata \textstyle x.
när du använder ZCA blekning (till skillnad från PCA blekning), vi brukar hålla alla \textstyle n dimensioner av data, och inte försöka minska dess dimension.
Regularizaton
vid implementering av PCA-blekning eller ZCA-blekning i praktiken kommer ibland några av egenvärdena \ textstyle \ lambda_i att vara numeriskt nära 0, och därmed skalningssteget där vi delar med \sqrt{\lambda_i} skulle innebära att dividera med ett värde nära noll; detta kan leda till att data spränger (tar stora värden) eller på annat sätt är numeriskt instabila. I praktiken implementerar vi därför detta skalningssteg med en liten mängd regularisering och lägger till en liten konstant \ textstyle \ epsilon till egenvärdena innan de tar kvadratroten och inversen:
\ begin{align}x_ {\rm PCAwhite, i} = \ frac{x_ {\RM rot, i} } {\sqrt {\lambda_i + \epsilon}}.\end{align}
När \ textstyle x tar värden runt \textstyle, kan ett värde på \textstyle \epsilon \ ca 10^{-5} vara typiskt.
När det gäller bilder, lägger du till \textstyle \ epsilon här också effekten av en liten utjämning (eller lågpassfiltrering) inmatningsbilden. Detta har också en önskvärd effekt av att ta bort aliasing artefakter som orsakas av hur pixlar läggs ut i en bild, och kan förbättra funktionerna lärt (detaljer är utanför ramen för dessa anteckningar).
ZCA whitening är en form av förbehandling av data som kartlägger den från \textstyle x till \textstyle x_{\rm ZCAwhite}. Det visar sig att detta också är en grov modell av hur det biologiska ögat (näthinnan) bearbetar bilder. Specifikt, när ditt öga uppfattar bilder, kommer de flesta intilliggande ”pixlar” i ögat att uppleva mycket liknande värden, eftersom intilliggande delar av en bild tenderar att vara starkt korrelerade i intensitet. Det är alltså slöseri för ditt öga att behöva överföra varje pixel separat (via din optiska nerv) till din hjärna. Istället utför din näthinna en decorrelation operation (detta görs via retinala neuroner som beräknar en funktion som kallas ”on center, off surround/off center, on surround”) som liknar den som utförs av ZCA. Detta resulterar i en mindre redundant representation av ingångsbilden, som sedan överförs till din hjärna.
implementera PCA Whitening
i det här avsnittet sammanfattar vi PCA, PCA whitening och ZCA whitening algoritmer, och beskriver också hur du kan implementera dem med hjälp av effektiva linjära algebrabibliotek.
först måste vi se till att data har (ungefär) noll-medelvärde. För naturliga bilder uppnår vi detta (ungefär) genom att subtrahera medelvärdet för varje bildplåster.
Vi uppnår detta genom att beräkna medelvärdet för varje patch och subtrahera det för varje patch. I Matlab kan vi göra detta genom att använda
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);Därefter måste vi beräkna \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. Om du implementerar detta i Matlab (eller till och med om du implementerar detta i C++, Java, etc., men har tillgång till en effektiv linjär algebra bibliotek), gör det som en explicit summa är ineffektivt. Istället kan vi beräkna detta i ett fall som
sigma = x * x' / size(x, 2);(kontrollera matematiken själv för korrekthet.) Här antar vi att x är en datastruktur som innehåller ett träningsexempel per kolumn (så x är en \textstyle n-by-\textstyle m-matris).
därefter beräknar PCA egenvektorerna för \Sigma. Man kan göra detta med hjälp av Matlab eig-funktionen. Men eftersom \Sigma är en symmetrisk positiv halvbestämd matris är det mer numeriskt tillförlitligt att göra detta med svd-funktionen. Konkret, om du implementerar
= svd(sigma);då kommer matrisen U att innehålla egenvektorerna för \Sigma (en egenvektor per kolumn, sorterad i ordning från topp till botten egenvektor), och diagonala poster i matrisen S kommer att innehålla motsvarande egenvärden (även sorterade i minskande ordning). Matrisen V kommer att vara lika med U och kan ignoreras säkert.
(notera: Svd-funktionen beräknar faktiskt singularvektorerna och singularvärdena för en matris, som För det speciella fallet med en symmetrisk positiv halvbestämd matris-vilket är allt vi är bekymrade över här—är lika med dess egenvektorer och egenvärden. En fullständig diskussion om singulära vektorer vs. egenvektorer ligger utanför ramen för dessa anteckningar.)
slutligen kan du beräkna \ textstyle x_ {\rm rot} och \textstyle \ tilde{x} enligt följande:
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keepdetta ger din PCA-representation av data i termer av \textstyle \tilde{X} \i \Re^k. Förresten, om x är en\textstyle n-by-\textstyle m-matris som innehåller alla dina träningsdata, är detta en vektoriserad implementering, och uttrycken ovan fungerar också för att beräkna x_ {\rm rot} och \ tilde{x} för hela din träningsuppsättning på en gång. Den resulterande x_{\rm rot} och \tilde{x} kommer att ha en kolumn som motsvarar varje träningsexempel.
för att beräkna PCA whitened data \textstyle x_{\rm PCAwhite}, använd
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;eftersom s diagonal innehåller egenvärdena \textstyle \lambda_i, visar det sig vara ett kompakt sätt att beräkna \textstyle x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}} samtidigt för alla \textstyle i.
slutligen kan du också beräkna ZCA whitened data \textstyle x_{\RM zcawhite} som:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;