Vad är en ARIMAX-Modell?

vad är ARIMAX-modellen?

Om du har läst vår serie av blogg tutorials på modeller för att uppskatta tidsseriedata, är du redan bekant med 3 stora metoder-autoregression, glidande medelvärden och integration.

vad är det gemensamma temat i alla dessa modeller?

de förlitade sig enbart på en enda variabel.

en modell kan dock också ta hänsyn till mer än bara tidigare priser eller tidigare rester.

och dessa är de så kallade ”MAX”-modellerna, där ARMAX är den icke – integrerade versionen och ARIMAX-dess integrerade ekvivalent.

så i denna handledning kommer vi att utforska hur de ser ut och visa dig hur du implementerar dem i Python steg för steg.

Låt oss komma igång, ska vi?

Varför kallas ARMAX och ARIMAX ”MAX” – modeller?

namnen ARMAX och ARIMAX kommer som förlängningar av ARMA respektive ARIMA. X som läggs till i slutet står för ”exogen”. Med andra ord föreslår det att man lägger till en separat annan extern variabel för att mäta vår endogena variabel.

Armax-och ARIMAX-Modellekvationen:

eftersom den enda skillnaden mellan ARMAX och ARIMAX är att den ena är integrerad och den andra inte, kan vi undersöka en av dem och sedan markera hur den andra skulle skilja sig.

vi undersökte en integrerad modell i vår senaste bloggartikel (ARIMA), så låt oss se hur ekvationen för ARIMAX ser ut.

ΔPt =c+ßX+ϕ1 ΔPt-1 + θ1 ϵt-1+ϵt

naturligtvis ekvationen för ARMAX skulle vara samma sak, förutom att vi skulle använda den faktiska rörliga, säger P -, i stället för dess delta.

Pt = C + usci + usci 1 Pt-1 +usci 1 usci-1 + usci

bryta ner ARIMAX-ekvationen:

Vi kan tänka på ARMAX som ett speciellt fall av ARIMAX, där integrationsordningen är 0.

så, för resten av handledningen kommer vi att fokusera på ARIMAX.

och vi börjar med att bryta ner de olika delarna i den. Till att börja med representerar Pt och Pt-1 värdena under den aktuella perioden respektive 1 period sedan.

på samma sätt är exporten och exporten-1 feltermerna för samma två perioder. Och, självklart, c är bara en baslinje konstant faktor.

de två parametrarna, 2 och 1, uttrycker vilka delar av värdet Pt – 1 och fel 1 sista perioden är relevanta för att uppskatta den nuvarande.

Nu är de två nya tillskotten till modellen ”X” och dess koefficient XHamster. Precis som i enlighet med detta är det en koefficient som kommer att beräknas utifrån modellvalet och uppgifterna. Men hur är det med X?

Vad är en exogen variabel?

Tja, X är den exogena variabeln och det kan vara vilken variabel vi är intresserade av.

det kan vara en tidsvarierande mätning som inflationstakten eller priset på ett annat index. Eller en kategorisk variabel som skiljer de olika dagarna i veckan. Det kan också vara en boolesk redovisning för de speciella festliga perioderna. Slutligen kan det stå för en kombination av flera olika externa faktorer.

tanken är att det kan vara någon annan variabel eller variabler som kan påverka priserna, så länge vi har tillgängliga data.

sådana yttre faktorer är kända som exogena variabler i vår regression. Vi använder deras värden för att förutsäga och förklara den vi är intresserade av, vilket råkar vara aktuella priser i vårt fall.

hur man implementerar Armax-och ARIMAX-modeller i Python?

bekvämt nog kommer statsmodels-paketet med en metod som kallas ARIMA som är fullt kapabel att hantera sådana ytterligare ingångar.

vi börjar med att ange modellens egenskaper och modellens order:

När vi har gjort det måste vi också ange det exogena argumentet som heter”exog”.

värdet vi vill skicka måste vara en array av något slag eftersom vi vill ha värden associerade med varje tidsperiod.

till exempel kan vi använda s&p priser som denna exogena variabel, eftersom vi redan har dem i våra data.

nu är vi redo att passa en ARIMAX (1,1,1) modell.

se till att namnge din modellvariabel på ett sätt som skiljer den från liknande modeller. I det här fallet väljer vi att göra detta genom att lägga till ”X, spx”i slutet för att indikera att den exogena variabeln är S&P.

sedan, som framgår av snippets, ställer vi detta lika med ARIMA-metoden som tidigare, vi lägger till tidsserien och ordningen, som vi är vana vid. Slutligen, mellan de två, ställer vi in” exog ”- argumentet lika med” DF SPX”, vilket indikerar s&p-priser.

om vi passar den här modellen och skriver ut sin sammanfattande tabell kommer vi att se att vi får en extra rad för s&p priser.

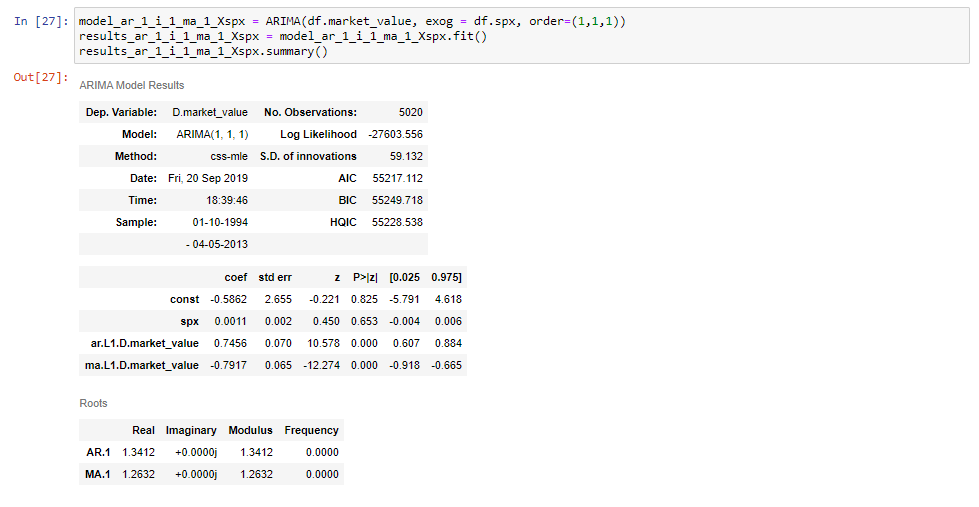
och det är allt som finns!

vi har framgångsrikt sett hur man implementerar en ARIMAX-modell i Python.

Om du vill lära dig mer om ARIMAX och andra tidsseriemodeller i Python, se till att kolla in våra steg-för-steg Python-handledning. Om du är ny på Python, och du är entusiastisk över att lära dig mer, kommer den här omfattande artikeln om att lära dig Python-programmering att vägleda dig hela vägen från installationen, genom Python-IDE, bibliotek och ramar, till de bästa Python-karriärvägarna och jobbutsikterna.

redo att ta nästa steg mot en karriär inom datavetenskap?

kolla in det fullständiga Datavetenskapsprogrammet idag. Börja med grunderna med vår statistik, matematik och Excel kurser. Bygg upp en steg-för-steg-upplevelse med SQL, Python, R, Power BI och Tableau. Och uppgradera din kompetens med maskininlärning, djupinlärning, Kreditriskmodellering, tidsserieanalys och kundanalys i Python. Fortfarande inte säker på att du vill göra ditt intresse för datavetenskap till en karriär? Du kan utforska läroplanen eller registrera dig för 15 timmars nybörjare till avancerat videoinnehåll gratis genom att klicka på knappen nedan.