6.11: Nachweis ungepaarter Elektronen

Es gibt experimentelle Methoden zum Nachweis ungepaarter Elektronen. Eines der Kennzeichen ungepaarter Elektronen in Materialien ist die Wechselwirkung mit einem Magnetfeld. Diese Wechselwirkung kann verwendet werden, um Informationen über Verbindungen bereitzustellen, die ungepaarte Elektronen enthalten.

Elektronenparamagnetische Resonanz

Elektronenparamagnetische Resonanz (EPR) oder Elektronenspinresonanz (ESR) ist eine spektroskopische Methode. Es hängt von der energetischen Trennung zweier Spinzustände ab, die nur in Gegenwart eines Magnetfeldes existiert.

EPR ist sehr eng mit einer anderen gängigen Art der Spinresonanzspektroskopie, der NMR, verwandt.

Spin ist eine Quanteneigenschaft, die keine wirkliche Analogie hat, die für uns auf makroskopischer Ebene sinnvoll wäre. Wir wissen jedoch, dass Spin magnetische Eigenschaften hat. Ein Elektron kann einen von zwei Werten für diese magnetischen Eigenschaften haben. Für diese Werte gibt es verschiedene Bezeichnungen: manchmal „oben“ und „unten“, manchmal +1/2 und -1 / 2. Welcher Spinwert ein Elektron besitzt, macht jedoch energetisch keinen Unterschied.

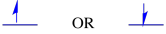
Die beiden möglichen Spinzustände sind energetisch gleich – es sei denn, ein Magnetfeld ist vorhanden. Sobald diese Situation eintritt, gibt es eine energetische Trennung zwischen den beiden Zuständen.

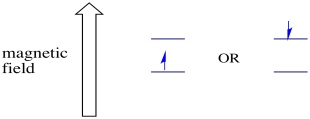
In Gegenwart eines Magnetfeldes trennen sich die beiden Spinzustände in zwei verschiedene Energieniveaus. Der Abstand zwischen den Energieniveaus hängt von der Größe des Magnetfelds ab. Je stärker das Magnetfeld, desto größer die Trennung.

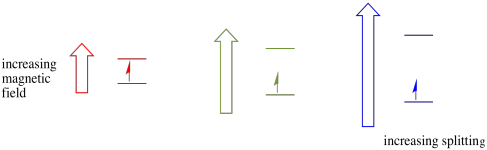
Dieser Fall gilt nur für ungepaarte Spins. Denken Sie daran, dass ungepaarte Spins mit einem Magnetfeld interagieren. Wenn alles Spin-gepaart ist, passiert nichts. Das ist sehr nützlich, weil es uns eine Möglichkeit gibt, diese ungepaarten Elektronen nachzuweisen.

Ein Elektron in einem Spinzustand kann durch die Absorption eines Photons noch zum anderen angeregt werden. Alternativ kann ein Elektron im höheren Zustand auf das niedrigere abfallen, wenn es ein Photon freisetzt.

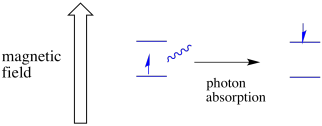
Damit dies geschieht, muss die Energie des Photons genau mit der Energiedifferenz zwischen den Zuständen übereinstimmen. Diese Goldilocks-Regel wird als Resonanzbedingung bezeichnet. Die Menge an Energie, die zugeführt wird, um von einem Energieniveau zum nächsten zu springen, muss genau richtig sein. Zu wenig Energie und das Elektron wird es nicht schaffen. Zu viel Energie und das Elektron wird es auch nicht schaffen. Es wartet nur auf das richtige Photon.

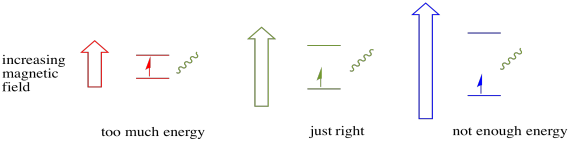
Wie viel Energie hat ein Photon? Erinnere dich an deine Planck-Einstein-Beziehung. Es beschrieb die Energie eines Photons:

\(E=h \nu \)

E ist die Energie des Photons, h ist die Plancksche Konstante (6,625 x 10-34 Js) und ν ist die Frequenz des Photons (es sieht aus wie ein römisches vee, aber es ist der griechische Buchstabe nu).

Alternativ, wegen der Beziehung zwischen Wellenlänge und Frequenz:

\(E= \frac{hc}{\lambda}\)

Die neuen Größen sind c, die Lichtgeschwindigkeit (3,0 x 108 m s-1) und λ, die Wellenlänge des Photons.

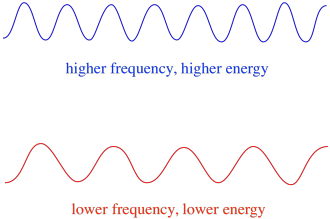
Im Allgemeinen liefern unterschiedliche Lichtwellenlängen unterschiedliche Energiemengen. Blaues Licht mit einer Wellenlänge nahe 475 nm hat mehr Energie als rotes Licht mit einer Wellenlänge nahe 700 nm.

In der EPR ist der allgemeine Bereich elektromagnetischer Strahlung oder die allgemeine Art von Photon Mikrowellenstrahlung. Die Frequenz dieser Photonen beträgt etwa 9 oder 10 GHz. (Eine andere Art der Spektroskopie, Rotationsspektroskopie, misst auch die Absorption von Mikrowellen. Es verwendet typischerweise etwas höhere Frequenzen von Mikrowellen. Rotationsspektroskopie liefert strukturelle oder Bindungsinformationen über Moleküle in der Gasphase.)

Abhängig von der Umgebung des ungepaarten Elektrons kann es anfälliger oder weniger anfällig für den Einfluss des externen Magnetfelds sein. Das bedeutet, dass die Energieaufteilung zwischen den beiden Spinzuständen von Molekül zu Molekül unterschiedlich ist. Infolgedessen würden verschiedene Moleküle im selben Magnetfeld unterschiedliche Wellenlängen der Mikrowellenstrahlung absorbieren.

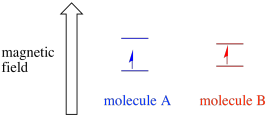
Normalerweise ist ein EPR-Spektrometer so ausgelegt, dass es der Probe eine feste Wellenlänge der Mikrowellenstrahlung liefert. Das Magnetfeld wird eingestellt und das Gerät misst, welche Feldstärke für die Absorption der Photonen erforderlich war. Ein EPR-Spektrum zeigt die Absorption als Funktion der magnetischen Feldstärke.

Es ist etwas anders, wie EPR-Spektren normalerweise angezeigt werden. Es wird als Ableitung des oben gezeigten Diagramms angezeigt. Das liegt an der Art und Weise, wie das Instrument die Änderung der Extinktion misst, wenn es das Magnetfeld ändert; dh es misst d (Absorption) / d (Magnetfeld). Das ist die Steigung des vorherigen Diagramms.

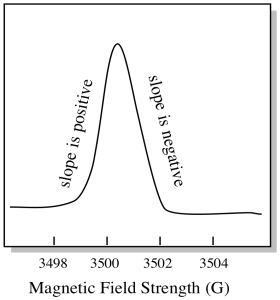
Infolgedessen sieht ein EPR-Spektrum wirklich eher so aus. Der Teil über der Grundlinie spiegelt die positive Steigung im vorherigen Diagramm wider. Der Teil unterhalb der Grundlinie spiegelt die negative Steigung im vorherigen Diagramm wider.

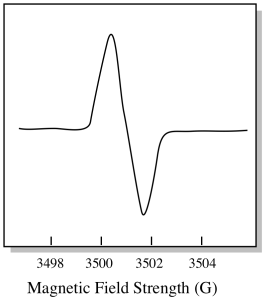
Die magnetische Feldstärke ist normalerweise nicht der Wert, der für die Spitzenposition gemeldet wird. Stattdessen wird der sogenannte g-Wert gemeldet. Der g-Wert ergibt sich aus der Gleichung für den Zeeman-Effekt (die Wirkung des Magnetfeldes auf die Aufteilung zwischen den Spin-Energieniveaus). Diese Beziehung ist:

\(\Delta E = g \beta B\)

wobei ΔE die Energiedifferenz zwischen Spinzuständen ist, g der g-Wert ist, eine Proportionalitätskonstante, die davon abhängt, wie anfällig das Elektron für den Einfluss des Magnetfelds ist, β das Bohr-Magneton (9,274 x 10-24 J T-1) und B das angelegte Magnetfeld ist.

Das bedeutet, dass für die Photonenabsorption

\(h \nu = g \beta B\)

und so

\(g = \frac{ h \nu}{\beta B}\)

Denken Sie daran, h und β sind nur Konstanten. Das heißt, g ist ein Maß für das Verhältnis des absorbierten Photons zum verwendeten Magnetfeld. Es ist ein Standardisierungsschritt. Wenn Menschen Instrumente haben, die leicht unterschiedliche Wellenlängen der Mikrowellenstrahlung verwenden, stimmen die Magnetfelder, die sie für dieselben Proben messen, nicht überein. Wenn jeder nur das Verhältnis von Wellenlänge zu Feldstärke misst, sollte sich alles ausgleichen. Der g-Wert ist ein reproduzierbares Maß für die Umgebung eines Elektrons, das von einem Labor zum anderen gleich sein sollte.Eine ähnliche Praxis wird in der NMR-Spektroskopie aus ähnlichen Gründen verwendet. Wenn wir eine chemische Verschiebung in ppm anstelle von Hz melden, korrigieren wir die Stärke des Magnetfelds in dem von uns verwendeten Instrument. Andernfalls würde dieselbe Probe zwei verschiedene Verschiebungen auf zwei verschiedenen Instrumenten ergeben.

Kopplung in EPR

Kopplung ist ein Phänomen, bei dem Magnetfelder miteinander interagieren. In der EPR kommt die Kopplung aufgrund des Einflusses benachbarter Kerne auf das beobachtete Elektron zustande.

Zum Beispiel wissen Sie vielleicht bereits, dass der Kern eines Wasserstoffatoms einen ungepaarten Spin hat. Das ist die Basis der 1H-NMR-Spektroskopie. Wenn dieser Kern einen ungepaarten Spin hat, hat er ein zugehöriges Magnetfeld. Da der Wasserstoffkern entweder einen Spinwert von +1/2 oder -1/2 haben könnte, sind ihm zwei mögliche Magnetfelder zugeordnet.Ein nahe gelegenes Elektron, das sich in einem externen Magnetfeld befindet, könnte sich nun in einer von zwei verschiedenen Situationen befinden. Entweder fügt das benachbarte Proton ein wenig zum Magnetfeld hinzu, oder es subtrahiert ein wenig vom äußeren Feld.

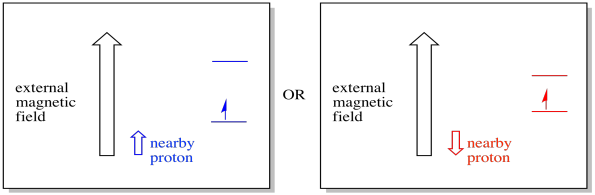
Infolgedessen kann das Elektron zwei verschiedene Felder erfahren. Denken Sie daran, wir haben es in der Spektroskopie nicht mit einem einzigen Molekül zu tun. Wir haben es mit einer großen Anzahl von Molekülen zu tun. Einige der Moleküle werden in einer Situation sein. Einige der Moleküle werden in der anderen Situation sein. Wir werden beide Situationen sehen. Es wird eine Absorption bei zwei verschiedenen Magnetfeldstärken geben.

Infolgedessen zeigt das EPR-Spektrum zwei Peaks wie folgt:

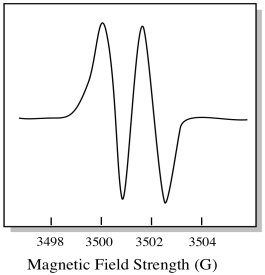
Diese Art von Peak im Spektrum wird wegen der doppelten Absorption als Dublett bezeichnet. Diese Eigenschaft eines EPR-Peaks wird als Multiplizität bezeichnet. In wie viele Zeilen ist der Peak aufgeteilt? Zwei. Es ist ein Dublett.

Die Dinge sind noch interessanter, wenn zwei Protonen in der Nähe sind. In diesem Fall haben beide benachbarten Protonen Spin. Jeder Spin könnte Wert haben +1/2 oder -1/2. Vielleicht sind sie beide +1/2. Vielleicht sind sie beide -1 / 2. Vielleicht gibt es einen von jedem. Diese drei möglichen Kombinationen haben drei verschiedene Auswirkungen auf das Magnetfeld, das das Elektron erfährt.

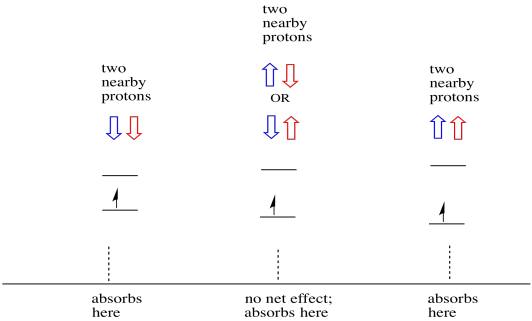
Infolgedessen gibt es drei Peaks im Spektrum. Das Spektrum wird als Triplett bezeichnet. Dieses Triplett ist unten unter dem Diagramm dargestellt, das die Spinkombinationen der benachbarten Wasserstoffatome veranschaulicht.

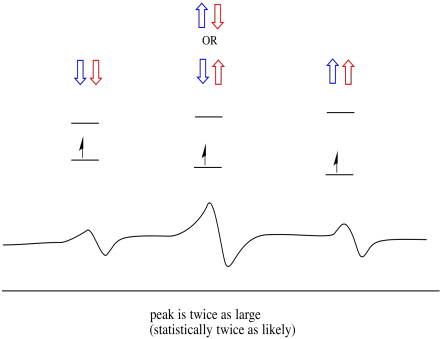
Beachten Sie, dass es zwei Möglichkeiten gibt, zu diesem mittleren Zustand zu gelangen, da entweder Wasserstoff in der gemischten Kombination auf oder ab sein kann. Diese Kombination ist doppelt so wahrscheinlich wie die beiden anderen, da es nur einen Weg gibt, diese Kombination zu erhalten: Die Spins beider Wasserstoffatome sind in einem Fall erhöht. Beide Wasserstoffatome sind in der anderen unten. Infolgedessen ist der mittlere Peak in einem Triplett doppelt so groß wie die Peaks an den Kanten.

Kopplung an Metallionen

Viele Kerne außer Wasserstoff haben einen Netto-Spin. Wenn das ungepaarte Elektron zufällig auf einem Metall gefunden wird, kann das EPR-Spektrum eine Bestätigung dieser Strukturinformation liefern. Diese Bestätigung kann sowohl aus der Magnetfeldinformation (ähnlich der chemischen Verschiebung in NMR) als auch aus der Multiplizität stammen.

Kernspins ausgewählter Metalle sind unten dargestellt.

Metall	Spin
V	7/2
Mn	5/2
Fe	0
Co	7/2
Cu	3/2

In jedem dieser Metalle hat der Kern unterschiedliche mögliche Magnetfelder. Beachten Sie, dass ihre Wirkungen etwas komplizierter sind als die eines Wasserstoffatoms. Zum Beispiel wirkt Kupfer mit Spin 3/2 in Bezug auf seine Wirkung auf das EPR-Spektrum eines nahe gelegenen Elektroms ein wenig wie drei verschiedene Wasserstoffkerne (jeweils mit Spin +/- 1/2). Die Vielzahl eines ungepaarten Elektrons an einem Kupferion sollte ziemlich ausgeprägt sein.

Manchmal sind die Dinge komplizierter, weil verschiedene Isotope desselben Elements unterschiedliche mögliche Spinwerte haben können. Tatsächlich trifft dies auf Wasserstoff und Kohlenstoff zu, aber die große Mehrheit des Wasserstoffs wird als 1H gefunden, so dass wir uns im Allgemeinen vorstellen können, dass er Spin = 1/2 hat; Die große Mehrheit des Kohlenstoffs ist 12C mit Spin = 0.

Die natürlichen Isotope des Eisens und ihre Kernspins sind in der folgenden Tabelle dargestellt.

Isotope	Spin	% Abundance
54Fe	0	5.9
56Fe	0	91.8
57Fe	1/2	2.1
58Fe	0	0.2

The EPR spectrum of an unpaired electron on iron may be slightly more complicated than we first thought. Innerhalb der Probe würden sich einige der Elektronen auf Eisenionen mit Spin = 1/2 befinden, die meisten jedoch nicht. Diese Komplikation kann ausreichen, um eine leichte Variation im Erscheinungsbild des Spektrums einzuführen, aber insgesamt würde es immer noch ziemlich wie ein Singulett aussehen.

In vielen Fällen werden die Dinge jedoch viel komplexer. Molybdän ist ein gutes Beispiel.

Isotop	Spin	% Fülle
92Mo	0	14.8
94Mo	0	9.3
95Mo	5/2	15,9
96Mo	0	16,7
97Mo	5/2	9,6
98Mo	0	24.1
100Mo	0

Es gibt sieben natürlich vorkommende Isotope von Molybdän. Fünf von ihnen haben Spin = 0, so dass ein ungepaartes Elektron auf diesen Isotopen zu einem einfachen Singulett im EPR-Spektrum führen würde. Die anderen beiden Isotope, die 25% der Gesamtmenge ausmachen, haben Spin = 5/2. Die meisten ungepaarten Elektronen auf Molybdän würden sich als Singulett zeigen. Ein bedeutender Teil würde sich jedoch als Sextett zeigen. Das bedeutet, dass im Idealfall ein ungepaartes Elektron auf Molybdän zu einem Singulett mit einem überlagerten Sextett führen würde (etwa ein Viertel so stark wie das Singulett).

Diese Situation könnte ungefähr so aussehen wie die Zeichnung unten.

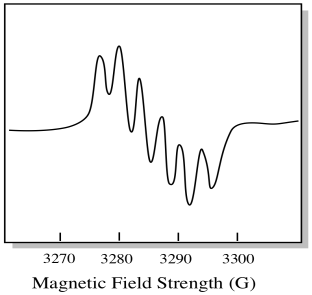
In Wirklichkeit sind EPR-Spektren in vielen Fällen enorm kompliziert. Sie sehen oft wie unscharfe Blobs aus. Es gibt so viele Dinge, die mit so vielen anderen Dingen zusammenhängen, dass es fast unmöglich wird, sie mit dem Auge zu entziffern. In den meisten Fällen werden Computersimulationen durchgeführt und die experimentellen Daten mit den Computersimulationen verglichen, um strukturelle Einblicke zu erhalten.

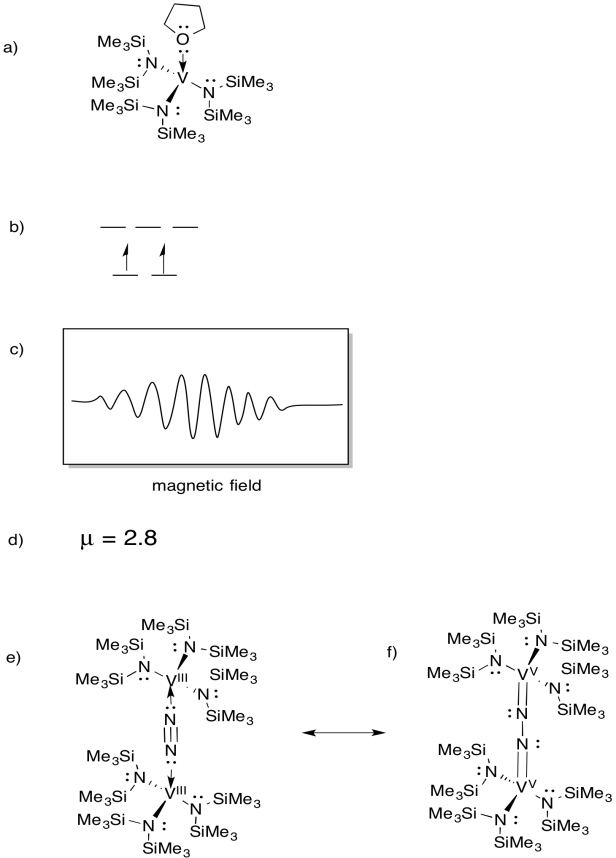
EPR-Spektren zur Verfügung gestellt von Virtual Imagination / Slapdash Chemistry Creations.