6.11: Détection d’électrons Non appariés

Il existe des méthodes expérimentales pour la détection d’électrons non appariés. L’une des caractéristiques des électrons non appariés dans les matériaux est l’interaction avec un champ magnétique. Cette interaction peut être utilisée pour fournir des informations sur les composés contenant des électrons non appariés.

La résonance paramagnétique électronique

La résonance paramagnétique électronique (RPE) ou résonance de spin électronique (RSE) est une méthode spectroscopique. Cela dépend de la séparation énergétique de deux états de spin qui n’existent qu’en présence d’un champ magnétique.

La RPE est très étroitement liée à un autre type courant de spectroscopie par résonance de spin, la RMN.

Le spin est une propriété quantique qui n’a pas d’analogie réelle qui aurait un sens pour nous au niveau macroscopique. Cependant, nous savons que le spin lui a associé des propriétés magnétiques. Un électron peut avoir l’une des deux valeurs de ces propriétés magnétiques. Il existe différentes étiquettes données à ces valeurs: parfois « haut » et « bas », parfois, +1/2 et -1 / 2. Cependant, quelle que soit la valeur de spin que possède un électron ne fait aucune différence énergétiquement.

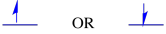
Les deux états de spin possibles sont les mêmes énergétiquement unless à moins qu’un champ magnétique ne soit présent. Une fois que cette situation se présente, il y a une séparation énergétique entre les deux États.

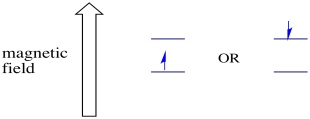
En présence d’un champ magnétique, les deux états de spin se séparent en deux niveaux d’énergie différents. La quantité de séparation entre les niveaux d’énergie dépend de l’amplitude du champ magnétique. Plus le champ magnétique est fort, plus la séparation est grande.

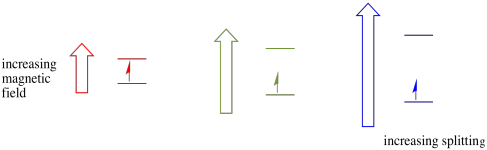
Ce cas n’est vrai que pour les spins non appariés. N’oubliez pas que les spins non appariés interagissent avec un champ magnétique. Si tout est jumelé, rien ne se passe. C’est très utile, car cela nous donne un moyen de détecter ces électrons non appariés.

Un électron dans un état de spin peut encore être excité à l’autre par l’absorbance d’un photon. Alternativement, un électron à l’état supérieur peut descendre à l’état inférieur s’il libère un photon.

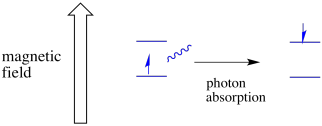
Pour que cela se produise, l’énergie du photon doit correspondre exactement à la différence d’énergie entre les états. Cette règle de Boucle d’or s’appelle la condition de résonance. La quantité d’énergie fournie pour passer d’un niveau d’énergie à l’autre doit être juste. Trop peu d’énergie et l’électron n’y arrivera pas. Trop d’énergie et l’électron ne le fera pas non plus. Il attend juste le bon photon.

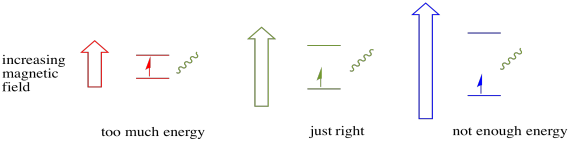
Combien d’énergie un photon a-t-il ? Rappelez-vous votre relation Planck-Einstein. Il décrit l’énergie d’un photon:

\(E =h\nu\)

E est l’énergie du photon, h est la constante de Planck (6,625 x 10-34 Js) et ν est la fréquence du photon (cela ressemble à un vé romain, mais c’est la lettre grecque, nu).

Alternativement, en raison de la relation entre la longueur d’onde et la fréquence:

\(E=\frac{hc}{\lambda}\)

Les nouvelles grandeurs sont c, la vitesse de la lumière (3,0 x 108 m s-1) et λ, la longueur d’onde du photon.

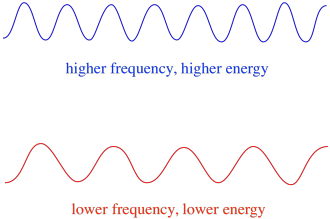
Ainsi, en général, différentes longueurs d’onde de la lumière fournissent différentes quantités d’énergie. La lumière bleue, d’une longueur d’onde proche de 475 nm, a plus d’énergie que la lumière rouge, d’une longueur d’onde proche de 700 nm.

En EPR, la gamme générale du rayonnement électromagnétique, ou le type général de photon, est le rayonnement micro-ondes. La fréquence de ces photons est d’environ 9 ou 10 GHz. (Un autre type de spectroscopie, la spectroscopie rotationnelle, mesure également l’absorbance des micro-ondes. Il utilise généralement des fréquences un peu plus élevées de micro-ondes. La spectroscopie rotationnelle donne des informations structurelles ou de liaison sur les molécules en phase gazeuse.)

Selon l’environnement de l’électron non apparié, il peut être plus ou moins sensible à l’influence du champ magnétique externe. Cela signifie que la division d’énergie entre les deux états de spin variera d’une molécule à l’autre. En conséquence, différentes molécules dans le même champ magnétique absorberaient différentes longueurs d’onde du rayonnement micro-ondes.

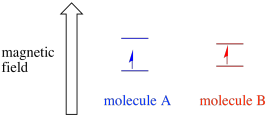
Habituellement, un spectromètre EPR est conçu de manière à fournir une longueur d’onde fixe de rayonnement micro-ondes à l’échantillon. Le champ magnétique est ajusté et l’instrument mesure l’intensité du champ nécessaire à l’absorption des photons. Un spectre EPR montre l’absorbance en fonction de l’intensité du champ magnétique.

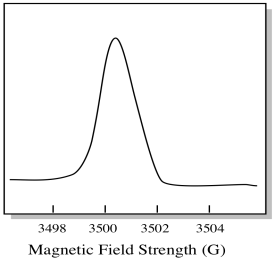
Il y a quelque chose d’un peu différent dans la façon dont les spectres EPR sont généralement affichés. Il est affiché comme un dérivé de l’intrigue ci-dessus. C’est à cause de la façon dont l’instrument mesure le changement d’absorbance lorsqu’il modifie le champ magnétique; c’est-à-dire qu’il mesure d (absorbance) / d (champ magnétique). C’est la pente de l’intrigue précédente.

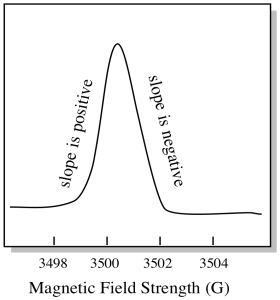
En conséquence, un spectre EPR ressemble vraiment plus à ceci. La partie au-dessus de la ligne de base reflète la pente positive dans le graphique précédent. La partie en dessous de la ligne de base reflète la pente négative dans le graphique précédent.

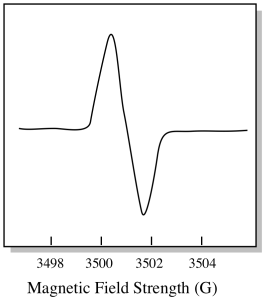
L’intensité du champ magnétique n’est généralement pas la valeur indiquée pour la position de crête. Au lieu de cela, quelque chose appelé la valeur g est signalé. La valeur g provient de l’équation de l’effet Zeeman (l’effet du champ magnétique sur la division entre les niveaux d’énergie de spin). Cette relation est :

\(\Delta E = g\beta B\)

dans laquelle ΔE est la différence d’énergie entre les états de spin, g est la valeur g, une constante de proportionnalité qui dépend de la sensibilité de l’électron à l’influence du champ magnétique, β est le magnéton de Bohr (9,274 x 10-24 J T-1) et B est le champ magnétique appliqué.

Cela signifie que, pour l’absorption de photons,

\(h\nu=g\beta B\)

et donc

\(g =\frac{h\nu}{\beta B}\)

Rappelez-vous, h et β ne sont que des constantes. Cela signifie que g est une mesure du rapport du photon absorbé au champ magnétique utilisé. C’est une étape de normalisation. Si les gens ont des instruments qui utilisent des longueurs d’onde légèrement différentes du rayonnement micro-ondes, les champs magnétiques qu’ils mesurent pour les mêmes échantillons ne seraient pas d’accord. Si tout le monde mesure simplement le rapport entre la longueur d’onde et l’intensité du champ, tout devrait s’égaliser. La valeur g est une mesure reproductible de l’environnement d’un électron qui devrait être le même d’un laboratoire à l’autre.

Une pratique similaire est utilisée en spectroscopie RMN, pour des raisons similaires. Lorsque nous signalons un déplacement chimique en ppm au lieu de Hz, nous corrigeons l’intensité du champ magnétique dans l’instrument que nous utilisons. Sinon, le même échantillon donnerait deux décalages différents sur deux instruments différents.

Couplage en EPR

Le couplage est un phénomène dans lequel les champs magnétiques interagissent les uns avec les autres. Dans l’EPR, le couplage est dû à l’influence des noyaux voisins sur l’électron observé.

Par exemple, vous savez peut-être déjà que le noyau d’un atome d’hydrogène a un spin non apparié. C’est la base de la spectroscopie RMN 1H. Si ce noyau a un spin non apparié, il a un champ magnétique associé. Parce que le noyau d’hydrogène pourrait avoir une valeur de spin, +1/2 ou -1 / 2, alors il a deux champs magnétiques possibles qui lui sont associés.

Un électron proche, placé dans un champ magnétique externe, pourrait maintenant se trouver dans l’une ou l’autre des deux situations différentes. Soit le proton voisin ajoute un peu au champ magnétique, soit il soustrait un peu du champ externe.

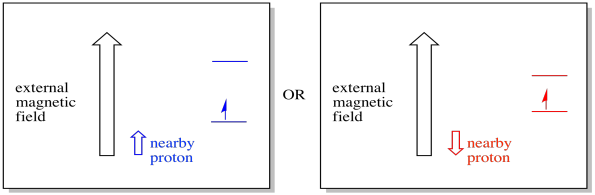
En conséquence, l’électron peut connaître deux champs différents. Rappelez-vous, nous n’avons pas affaire à une seule molécule en spectroscopie. Nous avons affaire à un grand nombre de molécules. Certaines des molécules seront dans une situation. Certaines molécules seront dans l’autre situation. Nous verrons les deux situations. Il y aura une absorbance à deux intensités de champ magnétique différentes.

En conséquence, le spectre EPR montre deux pics, comme ceci:

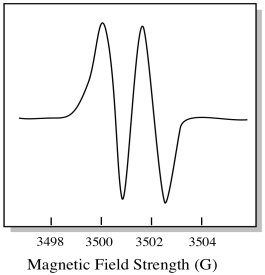
Ce type de pic dans le spectre est appelé doublet, en raison de la double absorbance. Cette caractéristique d’un pic EPR est appelée sa multiplicité. En combien de lignes le pic est-il divisé ? Deux. C’est un doublet.

Les choses sont encore plus intéressantes s’il y a deux protons proches. Dans ce cas, les deux protons voisins ont un spin. L’un ou l’autre spin pourrait avoir une valeur +1/2 ou -1 / 2. Peut-être qu’ils sont tous les deux +1/2. Peut-être qu’ils sont tous les deux -1 / 2. Peut-être qu’il y en a un de chacun. Ces trois combinaisons possibles auront trois effets différents sur le champ magnétique ressenti par l’électron.

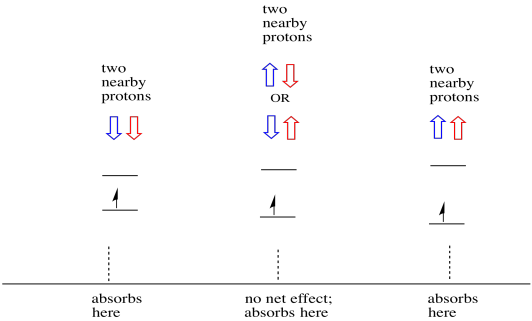
En conséquence, il y a trois pics dans le spectre. Le spectre est appelé un triplet. Ce triplet est représenté ci-dessous, sous le diagramme qui illustre les combinaisons de spin des hydrogènes voisins.

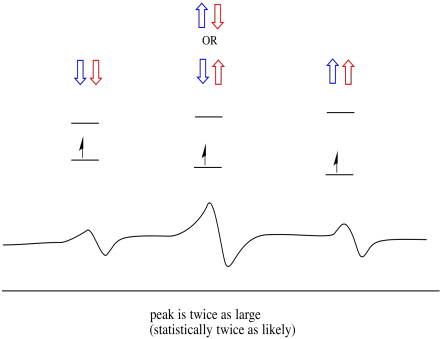
Notez que, comme l’hydrogène peut être haut ou bas dans la combinaison mixte, il existe deux façons d’arriver à cet état intermédiaire. Cette combinaison est deux fois plus probable que les deux autres, car il n’y a qu’une seule façon d’obtenir ces combinaisons: les spins des deux hydrogènes sont en hausse, dans un cas. Les deux hydrogènes sont dans l’autre. En conséquence, le pic moyen dans un triplet est deux fois plus grand que les pics sur les bords.

Couplage aux ions métalliques

Beaucoup de noyaux autres que l’hydrogène ont un spin net. Si l’électron non apparié se trouve sur un métal, le spectre EPR peut fournir une confirmation de ces informations structurelles. Cette confirmation peut provenir à la fois de l’information sur le champ magnétique (similaire au déplacement chimique en RMN) et de la multiplicité.

Les spins nucléaires des métaux sélectionnés sont indiqués ci-dessous.

V

Métal	Spin
7/2
Mn	5/2
Fe	0
Co	7/2
Cu	3/2

Dans chacun de ces métaux, le noyau a différents champs magnétiques possibles. Notez que leurs effets sont légèrement plus compliqués que ceux d’un atome d’hydrogène. Par exemple, le cuivre, avec un spin 3/2, agit un peu comme trois noyaux d’hydrogène différents (chacun avec un spin +/- 1/2) en termes d’effet sur le spectre EPR d’un électrom voisin. La multiplicité d’un électron non apparié sur un ion cuivre devrait être assez distinctive.

Parfois, les choses sont plus compliquées, car différents isotopes du même élément peuvent avoir des valeurs de spin différentes. En fait, c’est vrai avec l’hydrogène et le carbone, mais la grande majorité de l’hydrogène se trouve en 1H, donc en général on peut le considérer comme ayant spin = 1/2; la grande majorité du carbone est 12C, avec spin = 0.

Les isotopes naturels du fer et leurs spins nucléaires sont présentés dans le tableau ci-dessous.

Isotope	Spin	% Abundance
54Fe	0	5.9
56Fe	0	91.8
57Fe	1/2	2.1
58Fe	0	0.2

The EPR spectrum of an unpaired electron on iron may be slightly more complicated than we first thought. Dans l’échantillon, certains des électrons seraient situés sur des ions de fer avec un spin = 1/2, bien que la plupart ne le seraient pas. Cette complication peut suffire à introduire une légère variation dans l’apparence du spectre, mais dans l’ensemble, elle ressemblerait toujours à peu près à un singulet.

Cependant, dans de nombreux cas, les choses deviennent beaucoup plus complexes. Le molybdène en fournit un bon exemple.

Isotope	Spin	% Abondance
92Mo	0	14,8
94Mo	0	9.3
95Mo	5/2	15,9
96Mo	0	16,7
97Mo	5/2	9,6
98Mo	0	24,1
100Mo	0

Il existe sept isotopes naturels du molybdène. Cinq d’entre eux ont un spin = 0, donc un électron non apparié sur ces isotopes donnerait naissance à un simple singulet dans le spectre EPR. Les deux autres isotopes, représentant 25% du total, ont un spin = 5/2. La plupart des électrons non appariés sur le molybdène apparaîtraient comme un singulet. Cependant, une fraction importante apparaîtrait en tant que sextuor. Cela signifie que, dans un cas idéal, un électron non apparié sur le molybdène donnerait naissance à un singulet avec un sextuor superposé dessus (environ un quart aussi fort que le singulet).

Cette situation pourrait ressembler au dessin ci-dessous.

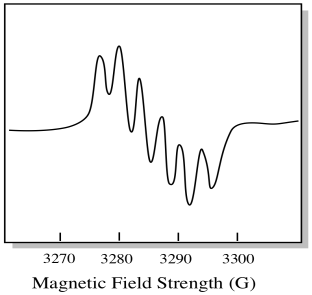
En réalité, les spectres EPR sont extrêmement compliqués dans de nombreux cas. Ils ressemblent souvent à des taches floues. Il y a tellement de choses qui se couplent à tant d’autres choses qu’il devient presque impossible de les déchiffrer à l’œil nu. Dans la plupart des cas, des simulations informatiques sont exécutées et les données expérimentales sont comparées aux simulations informatiques pour obtenir un aperçu structurel.

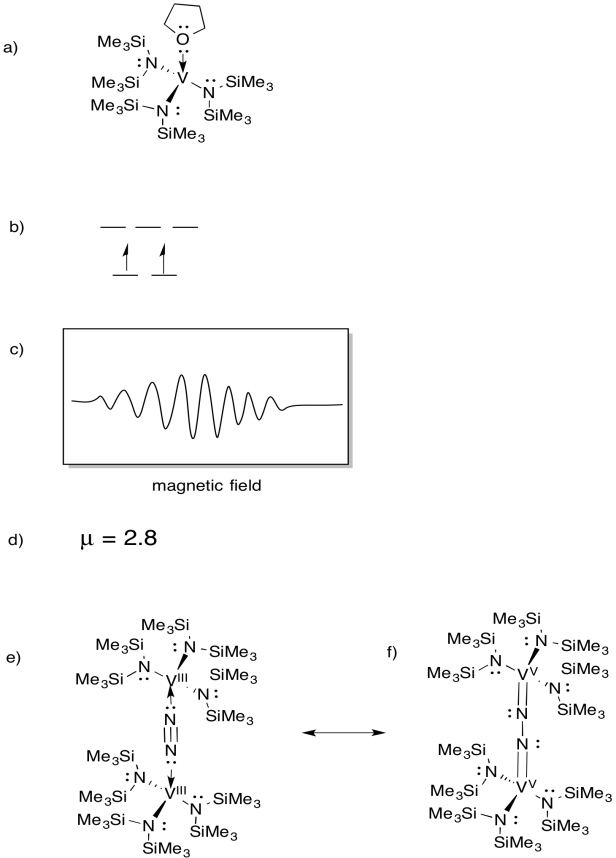
Spectres EPR fournis avec l’aimable autorisation de Virtual Imagination / Slapdash Chemistry Creations.